Изучая геометрию трапеции, мы сталкиваемся с интересным явлением - диагональю с углом. Это один из ключевых параметров, который влияет на форму и размеры данной геометрической фигуры. Но что на самом деле определяет эту диагональ и какие факторы играют роль в ее определении?
Несмотря на то что трапеция является достаточно простой фигурой, ее форма и свойства определяются рядом ключевых факторов. В частности, диагональ с углом является результатом взаимосвязи между длиной оснований и размером углов фигуры. Эти факторы влияют друг на друга, создавая уникальные соотношения и пропорции.
Однако, важно отметить, что величина диагонали также зависит от типа трапеции. В зависимости от относительных длин оснований и угла наклона, трапеция может быть прямоугольной, равнобедренной или произвольной. Это означает, что формула или метод определения диагонали будет различаться в каждом случае. Поэтому верное понимание этих основных категорий и правильная адаптация соответствующих формул имеют ключевое значение для определения размера диагонали.
Таким образом, чтобы полностью осознать, что определяет диагональ с углом в трапеции, необходимо учитывать все вышеперечисленные факторы, такие как длины оснований, размеры углов и тип фигуры. Только при учете всех этих параметров и использовании соответствующих формул мы сможем точно определить размер диагонали и полностью понять геометрию трапеции.
Влияние диагонали на углы в трапеции
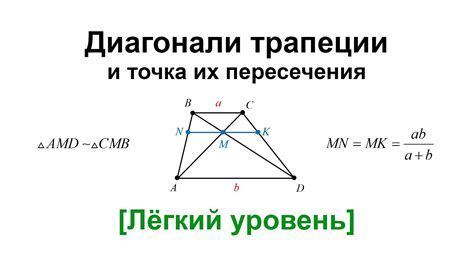
Влияние диагонали на углы трапеции:
Углы трапеции являются одним из ее основных характеристик и определяют ее форму и свойства. Для обозначения углов в трапеции используются различные нотации, такие как α, β, γ, δ и т.д. Изменение длины диагонали может привести к изменению величины углов и их соотношения внутри трапеции.
Соотношение длины диагонали и углов:
Длина диагонали трапеции может быть связана с ее углами через различные математические соотношения. Например, приращение длины диагонали может приводить к изменению углов в определенном соотношении, что позволяет нам получить новые значения углов.
Таким образом, диагональ влияет на углы в трапеции, изменение ее длины может привести к изменению величины углов и их соотношения внутри фигуры. Изучение данного взаимосвязи позволяет более глубоко понять и анализировать геометрические свойства трапеции.
Определение трапеции и ее особенности
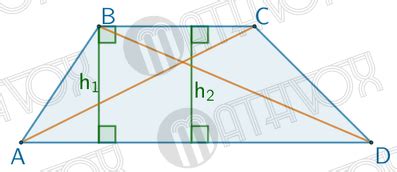
1. Базы трапеции: Стороны, которые параллельны друг другу, называются базами трапеции. Одна база является короче, а другая – длиннее. Базы играют важную роль при вычислении площади трапеции и других ее характеристик.
2. Боковые стороны: Две непараллельные стороны трапеции называются боковыми сторонами. Они связывают базы между собой и определяют форму фигуры.
3. Диагонали: Диагональ – это отрезок, соединяющий две несоседние вершины трапеции. Трапеция имеет две диагонали, которые пересекаются в точке называемой точкой пересечения диагоналей.
4. Углы: Трапеция имеет четыре угла. Углы, образованные базами и боковыми сторонами, называются углами трапеции. Один из углов может быть прямым, остальные углы являются тупыми или острыми.
5. Свойства: Трапеция обладает рядом интересных свойств. Например, сумма углов трапеции всегда равняется 360 градусам. Также, если в трапеции одна из диагоналей является высотой, то это прямоугольная трапеция. Эти и другие свойства помогают нам анализировать и решать задачи, связанные с трапециями.
Теперь, имея представление об определении трапеции и ее особенностях, мы можем более глубоко изучить эту фигуру и использовать ее свойства в практических задачах и вычислениях.
Роль пространственной линии в определении угловых особенностей трапеции

Применение диагонали в анализе трапеции позволяет не только определить ее угловые характеристики, но и выявить особые пропорции и соотношения между ее сторонами. Диагональ, которая соединяет вершины фигуры, играет важную роль в формировании основных элементов ее строения и позволяет установить взаимосвязь между углами и сторонами.
Структура трапеции предполагает, что диагонали являются линиями внутри фигуры, которые делят ее на два треугольника. Путем анализа соотношений между углами этих треугольников, определяются основные угловые характеристики трапеции, такие как углы при основаниях, углы при вершинах и дополнительные углы. Таким образом, диагональ играет роль ключевого элемента, с помощью которого определяются геометрические особенности трапеции.
| Символика | Описание |
|---|---|
| ∠ | Угол |
| ∆ | Треугольник |
Влияние пересечения диагонали на углы в трапеции: факторы определения
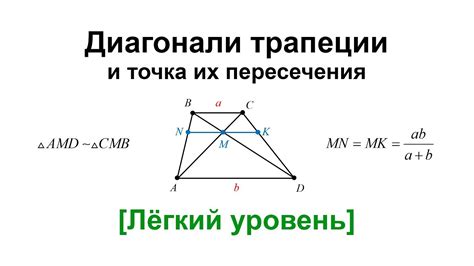
В данном разделе мы рассмотрим важность диагонали, которая пересекает трапецию, и ее влияние на углы, определяющие форму фигуры. Мы исследуем различные факторы, которые играют ключевую роль в определении величины углов, включая их взаимосвязь со сторонами и высотами трапеции.
Взаимосвязь диагоналей и углов:
Одним из основных факторов, влияющих на остроту или тупость углов в трапеции, является взаимосвязь между ее диагоналями. При пересечении внутренних диагоналей, углы трапеции могут изменять свои значения в зависимости от длины и угла пересечения.
Также важным фактором является параллельность оснований трапеции, которая определяет равность некоторых углов и их дополнений. Если основания трапеции параллельны, углы, расположенные на разных основаниях, будут суть недополняющими или дополняющими. Данная характеристика также будет взаимосвязана с длиной и углом пересечения диагонали.
Соотношение с высотами и сторонами:
Соотношение между диагональю и высотами трапеции также оказывает влияние на отношение углов. В случае, когда длина диагонали пропорциональна длине высоты, углы трапеции могут быть равными или близкими к равенству, что создает более симметричную форму фигуры.
Помимо этого, степень наклона сторон трапеции связана с распределением углов, и длина диагонали может влиять на данное распределение. Если диагональ является более горизонтальной, углы трапеции становятся более острыми, в то время как более вертикальная диагональ может создавать более тупые углы.
Таким образом, в контексте данного раздела мы обсудили важность пересечения диагоналей и их влияние на формирование углов в трапеции. Мы также рассмотрели взаимосвязь между углами, длиной диагонали, основаниями, высотами и сторонами фигуры. Понимание этих ключевых факторов позволяет более глубоко изучить свойства и особенности трапеции и их взаимосвязь.
Вопрос-ответ

Какая формула определяет диагональ с углом в трапеции?
Формула определения диагонали с углом (побочной диагонали) в трапеции выглядит следующим образом: d = √(a² + b² - 2ab*cos(γ)), где d - искомая диагональ, a и b - длины оснований трапеции, а γ - угол между ними.
Какое значение имеет угол γ для определения диагонали с углом в трапеции?
Угол γ используется для определения угла между основаниями трапеции. Этот угол влияет на длину побочной диагонали, так как он входит в формулу вычисления диагонали с углом.
Как влияет длина оснований трапеции на длину побочной диагонали?
Длина оснований трапеции прямо влияет на длину побочной диагонали. Чем больше разница в длине оснований, тем длиннее будет побочная диагональ. Если основания равны, то побочная диагональ будет равна нулю.
Что произойдет с длиной побочной диагонали, если угол между основаниями трапеции увеличится?
Если угол между основаниями трапеции увеличится, то длина побочной диагонали также увеличится. Это связано с тем, что угол влияет на позицию и наклон побочной диагонали, а следовательно, на ее длину.
Как изменится длина диагонали с углом в трапеции, если измениться только одно из оснований?
Если измениться только одно из оснований трапеции, то длина побочной диагонали не изменится. Это связано с тем, что формула для вычисления диагонали с углом зависит от разности длин оснований, а не от их абсолютных значений.
Как рассчитать длину диагонали с углом в трапеции?
Для рассчета длины диагонали с углом в трапеции необходимо знать значения длин оснований и угла, на который диагональ образует. Формула для расчета диагонали в трапеции выглядит следующим образом: d = √(a^2 + b^2 - 2abcosθ), где d - длина диагонали, a и b - длины оснований, θ - угол, на который диагональ образует с одним из оснований.



