Геометрия – древняя наука о фигурах и их свойствах, которая удивительным образом переплетается с математикой. Одним из основополагающих понятий в геометрии является угол – геометрическая фигура, образуемая двумя выходящими из одной точки полупрямыми.
Когда речь заходит о вычислении величины угла, возникает вопрос: как можно определить угол, даже если нет информации о его величине? Часто приходится прибегать к использованию тригонометрических функций, изображающих зависимости между углом и длинами сторон треугольника. Один из самых важных тригонометрических функций – это синус.
Синус – магическое слово, раскрывающее секреты углов. Он представляет собой отношение длины противоположной стороны к гипотенузе прямоугольного треугольника. Синонимом синуса можно назвать такую величину, которая помогает определить, насколько мал или велик угол. Зная эту величину, можно легко получить ответ на вопрос о величине самого угла, использовав соответствующую обратную функцию – арксинус.
Основные понятия и формулы для определения угла по его синусу
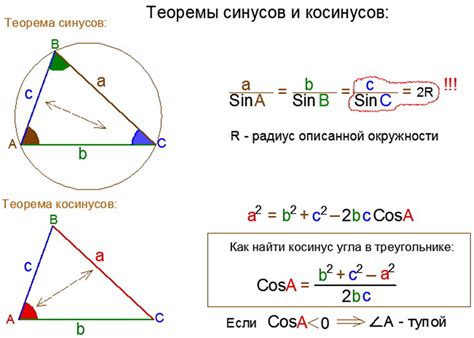
Синус угла можно определить как отношение смежной стороны треугольника к гипотенузе. Если обозначить значение синуса угла символом sin, смежную сторону как a и гипотенузу как h, то формула будет выглядеть следующим образом: sin α = a/h. Зная значения смежной стороны и гипотенузы, мы можем вычислить значение синуса угла.
Определение угла по его синусу можно провести обратным путем. Если известно значение синуса угла, мы можем определить сам угол с помощью обратной функции - арксинуса или sin-1. Такая формула будет выглядеть следующим образом: α = sin-1 (a/h). В качестве результата мы получим величину угла.
Математический подход: преобразование синуса в значение угла
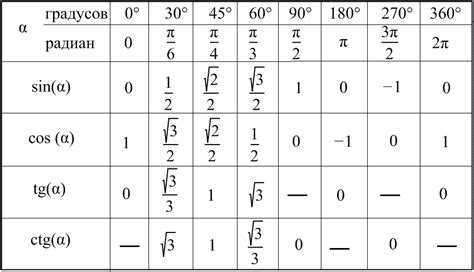
В мире математики существует особый подход, позволяющий определить значение угла по его синусу. Этот подход основан на рассмотрении связи между синусом и углом и использует специальные формулы и тригонометрические функции. С помощью такого математического преобразования можно получить точное значение угла, зная значение его синуса.
Для начала рассмотрим, что такое синус угла. Синус - это одна из тригонометрических функций, которая связывает длины сторон прямоугольного треугольника с углами. Он определяется как отношение противолежащего катета к гипотенузе данного треугольника. С помощью синуса мы можем выразить угол, зная значения этих длин сторон.
Для преобразования синуса в значение угла используется обратная функция - арксинус (asin). Арксинус умеет вычислять значение угла по его синусу. Таким образом, зная значение синуса угла, мы можем воспользоваться формулой арксинуса для получения значения самого угла.
Для удобства данная формула записывается следующим образом: угол = arcsin(синус), где arcsin - функция арксинуса, а синус - значение синуса угла. Используя это равенство, мы можем определить значение угла, зная его синус.
Рассмотрим пример. Допустим, у нас есть значение синуса угла, равное 0.5. С помощью формулы угол = arcsin(0.5), мы можем получить значение этого угла. Подставив 0.5 вместо синуса в формулу, мы получим значение угла, которое соответствует этому синусу.
Таким образом, математический подход позволяет определить значение угла по его синусу с помощью арксинуса. Этот метод основывается на преобразовании синуса в угол с использованием специальных функций и формул. Зная значение синуса угла, мы можем точно определить его величину и использовать эту информацию в различных математических и физических задачах.
Геометрический подход: применение треугольников для вычисления значения угла
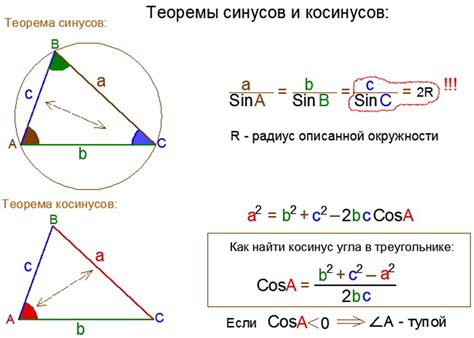
В геометрии существует эффективный метод определения величины угла, основанный на использовании свойств треугольников. Этот метод позволяет рассчитать угол, используя информацию о соотношениях его сторон или о синусе данного угла.
Используя данную геометрическую технику, мы можем определить угол без прямого измерения, если имеем информацию о длинах сторон треугольника или о значении синуса искомого угла.
Для использования этого метода необходимо знать основные свойства треугольников и формулы, связывающие углы и стороны. Например, известными нам могут быть формулы синуса, косинуса или теорема синусов, которые позволяют выражать соотношения между углами и сторонами треугольника.
Путем применения этих формул и свойств треугольников, мы можем решать задачи, связанные с определением величин углов, используя математический аппарат геометрии.
Таблицы и графики: эффективные инструменты для нахождения значения угла по синусу
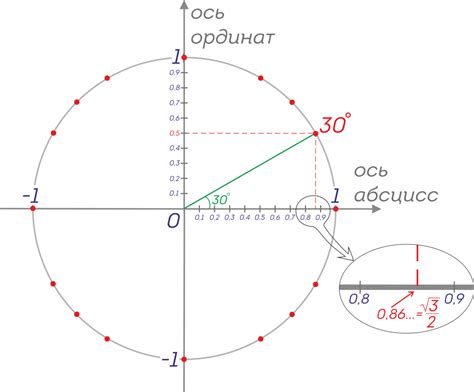
Таблицы представляют собой структурированные списки данных, в которых углы и их соответствующие синусы располагаются в упорядоченном виде. С помощью таблиц можно быстро и легко найти значение угла, зная его синус, используя простой поиск по таблице. Это особенно полезно при работе с углами, для которых уже имеются предварительно подготовленные таблицы.
- Графики представляют собой визуальное отображение зависимости между углом и его синусом на координатной плоскости. Они позволяют наглядно увидеть изменение значения угла в зависимости от изменения значения синуса. Проведя линию или кривую на графике, можно легко определить значение угла по известному значению синуса путем прочтения координаты на оси углов.
- При использовании таблиц и графиков очень важно учитывать их точность и надежность. Для этого необходимо использовать достоверные и проверенные источники данных, а также учитывать все возможные ограничения и условия задачи. Кроме того, необходимо учитывать предварительно вычисленные значения синуса угла, чтобы избежать погрешностей и ошибок при нахождении соответствующего угла.
- Таким образом, таблицы и графики являются полезными инструментами для нахождения значения угла по его синусу. Они облегчают процесс вычислений и делают его более наглядным и понятным. Правильное использование этих инструментов поможет эффективно решать геометрические задачи и получать точные результаты.
Практические примеры: подробная инструкция по определению значения угла через его синус
В этом разделе представлены практические примеры, которые помогут вам шаг за шагом освоить процесс определения величины угла по известному значению его синуса. Мы разберем различные ситуации и предоставим пошаговую инструкцию к вычислению угла, использовавши различные методы и подходы. Внимательно следуйте инструкциям и упражняйтесь, чтобы стать экспертом в определении угла через его синус.
- Пример 1: Определение угла в прямоугольном треугольнике
- Пример 2: Определение угла в остроугольном треугольнике
- Пример 3: Нахождение угла в применении к геометрическим фигурам
В этом примере мы узнаем, как вычислить величину угла в прямоугольном треугольнике, используя известное значение синуса угла. Мы обсудим конкретные шаги и формулы, которые помогут вам достичь точного результата. Предварительно известно только значение синуса угла, но после завершения примера вы сможете определить его величину.
В этом примере мы рассмотрим способы определения величины угла в остроугольном треугольнике, когда известно значение синуса этого угла. Мы проведем шаги по вычислению угла, используя отношения синуса, косинуса и тангенса, а также дадим пояснения и примеры, чтобы помочь вам лучше понять процесс. Практический пример поможет вам усвоить эту тему и применить ее в реальной жизни.
Этот пример сосредоточен на поиске величины угла с использованием синуса в контексте геометрических фигур. Мы рассмотрим примеры применения возможностей определения углов по значению их синусов в различных формах, включая треугольники, четырехугольники и окружности. Вы получите полезные инструкции по вычислению угла в каждом конкретном случае и узнаете, как применить эти знания в решении задач по геометрии.
Вопрос-ответ

Как определить величину угла по его синусу?
Для определения величины угла по его синусу можно воспользоваться обратным синусом, также известным как арксинус или sin-1. Применение функции арксинуса к заданному значению синуса даст результат в радианах. Чтобы получить ответ в градусах, умножьте результат на 180 и разделите на пи. Обратите внимание, что арксинус возвращает только значения в диапазоне от -π/2 до π/2.
Как рассчитать угол, зная его синус?
Если вам известно значение синуса угла, можно использовать арксинус (sin-1) для определения величины угла. Для этого примените функцию арксинуса к заданному значению и получите результат в радианах. Чтобы перевести результат в градусы, умножьте его на 180 и разделите на π. Учтите, что арксинус возвращает только значения в пределах от -π/2 до π/2.
Как определить угол по его синусу с помощью математических формул?
Если вам известно значение синуса угла, можно использовать обратную функцию синуса (sin-1 или арксинус) для определения величины угла. Формула для этого выглядит следующим образом: угол = arcsin(значение синуса). Результат будет в радианах, поэтому, если вам нужны градусы, умножьте его на 180 и разделите на π. Обратите внимание, что арксинус возвращает только значения в пределах от -π/2 до π/2.
Как определить значению угла по его синусу в градусах?
Если вам известно значение синуса угла и вы хотите определить его величину в градусах, вам потребуется применить обратную функцию синуса (sin-1 или арксинус) к заданному значению. Результат будет в радианах, поэтому умножьте его на 180 и разделите на π, чтобы получить значение в градусах.
Можно ли определить значение угла по его синусу без использования калькулятора?
Если вам известно значение синуса угла, можно определить его величину в градусах без использования калькулятора с помощью таблиц или специальных формул. Например, можно воспользоваться таблицей значений тригонометрических функций, где для каждого значению синуса указано соответствующее значение угла. Также можно использовать формулы соотношений между тригонометрическими функциями (например, sin^2 + cos^2 = 1), чтобы определить угол по заданному значению синуса.
Что такое синус угла и как его определить?
Синус угла - это отношение противоположной стороны треугольника к гипотенузе. Чтобы определить угол по его синусу, необходимо использовать обратную функцию - арксинус. Для этого нужно воспользоваться специальным калькулятором или таблицей значений синуса и его обратной функции.
Как можно вычислить угол, если известен только его синус?
Если у вас есть только значение синуса угла, то для определения самого угла необходимо воспользоваться арксинусом. То есть, применить обратную функцию синуса. Например, если синус угла равен 0,5, то угол будет примерно 30 градусов.



