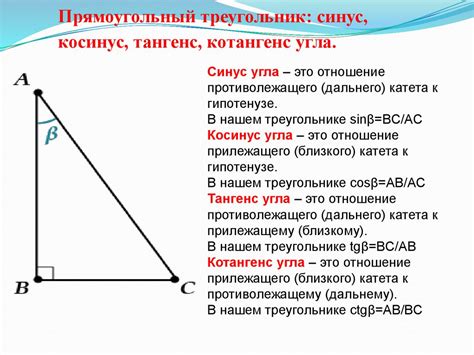
Введение: Пирог велик и разнообразен, и таковы же разнообразие и сложности, которые можно увидеть в геометрии. Одной из таких задач является нахождение значений синусов, косинусов и тангенсов углов треугольника или пирамиды. В этом разделе мы сосредоточимся на расчете тангенса угла 50 градусов и представим различные методы, которые может использовать читатель для этого. Приготовьтесь к увлекательному путешествию в мир геометрии и вычислений!
Мы начнем с простого: тангенс угла - это отношение противоположной стороны треугольника к прилежащей стороне. С этим определением можно легко определить тангенс угла 50 градусов. Однако, чтобы представить численное значение этого отношения, нам нужно использовать тригонометрические таблицы или калькулятор. В данной статье мы рассмотрим несколько альтернативных методов получения численного значения тангенса угла 50 градусов без использования дополнительных инструментов.
Метод 1: Используйте свойства треугольников и математические выкладки, чтобы найти числовое значение тангенса. Зная, что сумма углов треугольника равна 180 градусам, мы можем найти значение третьего угла, а затем применить соответствующие тригонометрические отношения для нахождения тангенса угла 50 градусов.
Основные понятия тангенса
| Тангенс | Синонимы |
| Прямая | Касательная |
| Отношение | Деление |
| Научная величина | Математическая абстракция |
Определение и основные свойства тангенса
В данном разделе мы рассмотрим понятие и основные характеристики тангенса, одной из важных математических функций, используемой для измерения соотношения сторон в треугольниках.
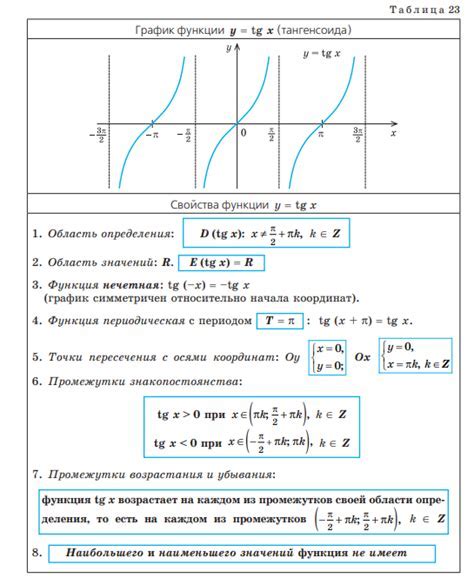
Тангенс является тригонометрической функцией, которая описывает отношение противоположной катета и прилежащей катета в прямоугольном треугольнике. Он широко используется в геометрии, физике, инженерии и других науках для решения различных задач связанных с углами и сторонами треугольников.
Основные свойства тангенса:
| Свойство | Описание |
|---|---|
| Периодичность | Тангенс функция является периодической с периодом π (пи). |
| Ограниченность | Значения тангенса находятся в пределах от минус бесконечности до плюс бесконечности, но функция тангенса имеет вертикальные асимптоты, где значения не определены. |
| Симметричность | Тангенс функция имеет симметрию относительно начала координат. |
| Асимптотическое поведение | Функция тангенса приближается к горизонтальным асимптотам при приближении к аргументу, равному кратному π (пи). |
| Периодичность отношения | Отношение тангенса углов суммы или разности равно тангенсу суммы или разности этих углов. |
Изучение и понимание свойств тангенса позволяет эффективно применять его для вычислений и решения задач в различных областях науки и техники.
Как вычислить значение тангенса для угла в 50 градусов?
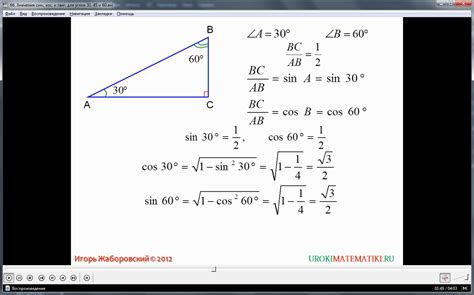
Согласно математическим свойствам, тангенс угла может быть определен как отношение синуса угла к косинусу угла. Другими словами, чтобы найти значение тангенса угла 50 градусов, необходимо вычислить синус и косинус данного угла, а затем разделить синус на косинус.
Воспользуемся тригонометрическими функциями:
- Найдем значение синуса угла 50 градусов: sin(50°) ≈ 0.7660
- Найдем значение косинуса угла 50 градусов: cos(50°) ≈ 0.6428
- Вычислим значение тангенса угла 50 градусов, делая отношение sin(50°) к cos(50°): tan(50°) ≈ 1.1918
Таким образом, тангенс угла 50 градусов равняется приблизительно 1.1918. Именно это значение вы получите при использовании метода вычисления через синус и косинус.
Геометрический метод нахождения значения тангенса угла

В геометрии существует метод, позволяющий определить значениe тангенса угла без применения математических формул и расчетов. Этот метод основан на изучении геометрических свойств треугольника и отношения сторон в нем.
Для определения значения тангенса угла, можно построить прямоугольный треугольник, у которого один угол равен заданному углу. Затем, следует провести перпендикулярную линию к противоположной стороне треугольника из вершины угла. Полученная отрезка будет основанием прямоугольный треугольник. Далее, с помощью простого отношения между сторонами треугольника можно найти значение тангенса угла.
Применение геометрического метода расчета тангенса угла особенно полезно в практических задачах, связанных с измерениями и построениями. Например, для нахождения высоты некоторого объекта по углу наклона можно использовать этот метод. Также, геометрический подход позволяет визуально представить математические концепции и упрощает понимание их сути.
Тригонометрический подход к определению тангенса

Рассмотрим пример: допустим, что у нас есть прямоугольный треугольник с гипотенузой, противолежащей катету, и углом между гипотенузой и катетом. Чтобы найти тангенс этого угла, нужно разделить длину противолежащего катета на длину прилежащего катета. Такой подход позволяет нам связать значения тангенса с геометрической формой треугольника и его углами.
- Треугольник ABC имеет гипотенузу AB, противолежащую углу С, и катет BC, прилежащий углу С.
- Тангенс угла С равен отношению длины противолежащего катета BC к длине прилежащего катета AB: тангенс угла С = BC / AB.
- Значение тангенса угла С будет числом, которое показывает, насколько отклоняется угол С от прямого угла: чем больше это число, тем круче наклон угла.
Тригонометрический способ расчета тангенса позволяет нам использовать геометрические принципы и отношения для определения значения тангенса угла без необходимости измерять угол непосредственно.
Практическое применение тангенса угла 50 градусов

В данном разделе рассмотрим применение значения тангенса угла 50 градусов в различных практических ситуациях. Это значение угла имеет важное значение в решении конкретных задач и проблем, и его применение позволяет решить сложные математические и геометрические задачи.
Конструкционное проектирование:
Знание тангенса угла 50 градусов позволяет инженерам и архитекторам оптимизировать и проектировать различные конструкции. Например, при проектировании устойчивых и надежных мостов, знание тангенса угла 50 градусов помогает определить оптимальную длину опор, чтобы обеспечить необходимую жесткость и устойчивость конструкции.
Судостроение и навигация:
В морской навигации знание тангенса угла 50 градусов используется для расчета пути и координат местоположения судна. Это позволяет морякам точно определить свое положение на море и учесть влияние течения и ветра для выбора наиболее безопасного пути.
Проектирование и определение высоты:
Знание тангенса угла 50 градусов применяется в геодезии и архитектуре для определения высоты и длины объектов. Например, архитектору при проектировании здания необходимо знать тангенс угла наклона крыши, чтобы правильно определить ее форму и высоту, а геодезистам он помогает в измерениях высот и расстояний.
В общественном и научном пространстве применение тангенса угла 50 градусов распространено в различных областях, позволяя решать задачи, связанные с расчетами, конструкциями и навигацией.
Определение высоты объекта с помощью тангенса

В данном разделе рассматривается метод определения высоты объекта, основанный на использовании тангенса.
Высота объекта является одним из важных параметров, которые можно вычислить с помощью геометрических функций. Нам понадобятся элементарные знания геометрии и тригонометрии для применения данного метода. Определение высоты объекта с помощью тангенса позволяет нам рассчитать этот параметр, используя угол наклона и расстояние до объекта.
Для расчета высоты объекта нам необходимо знать длину горизонтального расстояния от наблюдателя до объекта и угол наклона, который определяется отношением противоположной стороны и прилежащей стороны треугольника. Тангенс угла является основным понятием, используемым в этом методе. Он вычисляется как отношение противолежащей стороны к прилежащей стороне треугольника.
Применение тангенса позволяет нам определить высоту объекта, используя формулу вычисления противолежащей стороны треугольника. Зная длину горизонтального расстояния, мы можем использовать найденное значение тангенса угла для определения высоты объекта.
Пример использования данного метода включает определение высоты столба по известной длине расстояния от наблюдателя до столба и известному углу наклона. Расчеты могут быть выполнены с использованием тангенса угла с помощью представленной формулы.
Определение угла наклона плоскости с помощью тангенса
В геометрии угол наклона плоскости играет важную роль при определении ее ориентации в пространстве. Этот угол позволяет определить, как плоскость отклонена от горизонтального положения. В данном разделе рассмотрим способы определения угла наклона плоскости с помощью тангенса и приведем примеры его использования.
| Метод | Описание |
|---|---|
| Метод измерения | Для определения угла наклона плоскости можно использовать специальные инструменты, например, инклинометры или нивелиры. Измерьте угол между горизонтальной линией и плоскостью, применяя указанные инструменты. Этот угол будет являться углом наклона плоскости. |
| Метод расчета | Если вам известны координаты точек, лежащих на плоскости, вы можете вычислить угол наклона плоскости с помощью тангенса. Для этого найдите разность высот между точками и разность их горизонтальных расстояний. Затем примените формулу тангенса, разделив разность высот на разность горизонтальных расстояний. Полученное значение будет являться тангенсом угла наклона плоскости. |
| Пример использования тангенса | Предположим, у вас есть две точки A(2, 3) и B(5, 7), которые лежат на плоскости. Чтобы определить угол наклона плоскости, вычислим разность высот и разность горизонтальных расстояний между этими точками. Разница высот составляет 4, а разница горизонтальных расстояний - 3. Применяя формулу тангенса (тангенс угла наклона = разность высот / разность горизонтальных расстояний), получаем, что тангенс угла наклона этой плоскости равен 4/3. Таким образом, угол наклона плоскости составляет приблизительно 53.13 градуса. |
Исчисление значений величины при угле наклона 50°: практические задачи

В данном разделе рассмотрены практические примеры расчетов значения величины, связанной с углом наклона в 50°. Опишем ситуации, где необходимо использовать данное значение и приведем конкретные примеры решения задач.
В первом примере рассмотрим задачу на определение горизонтальной проекции скорости объекта, движущегося под углом 50° к горизонту. Найдем значение данной проекции, используя рассчитанный тангенс угла наклона.
Приведем второй пример, где требуется определить высоту дерева. При измерении было получено, что угол между горизонтом и линией визирования составляет 50°. С использованием значения тангенса этого угла, можно рассчитать искомую высоту дерева.
В следующем примере предлагается решить задачу на определение длины наклона горы. При измерении было получено, что угол наклона равен 50°. С использованием тангенса этого угла можно рассчитать искомую длину наклона горы.
Определение длины тени при известной высоте объекта

В данном разделе мы рассмотрим способы расчета длины тени, которую проецирует объект при заданной его высоте.
Перед тем, как приступить к расчетам, необходимо учесть, что высота объекта является одним из ключевых параметров для определения длины его тени. Высота объекта представляет собой вертикальное расстояние от его основания до верхней точки, и может быть выражена в метрах, сантиметрах, футах и т.д.
Чтобы определить длину тени, мы будем использовать геометрические принципы и формулы, основанные на соотношениях геометрических фигур. При расчете длины тени мы учтем, что необходимо знать расстояние от источника света до объекта, а также угол падения лучей света на объект.
Для более наглядного объяснения мы приведем примеры расчета длины тени при различных значениях высоты объекта. Здесь будет рассмотрено несколько ситуаций, включая объекты разной формы и положение источника света.
- Расчет длины тени для прямоугольного объекта
- Расчет длины тени для круглого объекта
- Расчет длины тени для объекта с нестандартной формой
Вопрос-ответ

Как вычислить тангенс угла 50 градусов?
Тангенс угла 50 градусов можно вычислить с помощью формулы: тангенс угла равен отношению противоположного катета к прилежащему катету в прямоугольном треугольнике. Для угла 50 градусов в прямоугольном треугольнике смежный катет равен прилежащему катету умноженному на тангенс угла, поэтому тангенс 50 градусов равен отношению противоположного катета к прилежащему катету.
Какую формулу использовать для вычисления тангенса угла 50 градусов?
Для вычисления тангенса угла 50 градусов используется формула тангенса: тангенс угла равен отношению противоположного катета к прилежащему катету в прямоугольном треугольнике.
Можно ли вычислить тангенс угла 50 градусов без прямоугольного треугольника?
Нет, для корректного вычисления тангенса угла 50 градусов необходимо иметь прямоугольный треугольник с известными значениями противоположного и прилежащего катетов.
Можете привести пример вычисления тангенса угла 50 градусов?
Конечно! Предположим, у нас есть прямоугольный треугольник, в котором противоположный катет равен 3 и прилежащий катет равен 4. Тогда тангенс угла 50 градусов будет равен отношению противоположного катета (3) к прилежащему катету (4), то есть 3/4.



