В мире геометрии существует таинственная область, где линии пересекаются и создают формы, в которых заключено гармоничное сочетание прямых углов и изогнутых контуров. Это мир углов, где математика сливается с эстетикой и формирует уникальные конструкции.
Углы - это символы, которые хранят тайну о равенстве, взаимопонимании и балансе. Они - ключевые элементы в искусстве измерений, позволяющие нам определить фигуры и строить прочные сооружения. С уверенностью можно сказать, что углы являются основой геометрии, которая олицетворяет порядок и форму в нашем мире.
Однако, углы не имеют однозначного лица - они настолько разнообразны, что способны изменить характер фигуры в одно мгновение. Они бывают острыми и тупыми, крутыми и прямыми, огибающими и режущими. Каждый угол обладает своими уникальными свойствами и функциями, отражая природу их различий.
Основные понятия геометрических углов

Вершина угла - это точка, или точка пересечения, где две линии или отрезка сходятся. Она обозначается буквой "В".
Стрелки - это две линии, которые исходят из вершины угла и образуют его область. Они могут быть прямыми, острыми или тупыми.
Размер угла - это мера его открытой области, которая измеряется в градусах. Размер угла может варьироваться от 0 до 360 градусов.
Смежные углы - это два угла, которые имеют общую вершину и одну общую сторону. Смежные углы часто встречаются в геометрии и могут использоваться для различных вычислений и конструкций.
Вертикальные углы - это пара углов, находящихся на противоположных сторонах пересекающихся прямых и имеющих равные размеры. Они образуются параллельными линиями или при пересечении.
Дополнительные углы - это пара углов, сумма которых равна 180 градусов. Эти углы могут быть любого размера и располагаются по разные стороны пересекающихся линий.
Понимание основных понятий углов позволяет лучше взаимодействовать с геометрическими фигурами и решать задачи, связанные с измерением и построением углов. Знание этих понятий также может быть полезным в архитектуре, инженерии, фотографии и других областях, где требуется точное понимание пространства и угловых отношений.
Геометрическая интерпретация углов

Раздел "Геометрическая интерпретация углов" позволяет раскрыть важные аспекты связанные с описанием и изучением углов в геометрии. В этом разделе мы рассмотрим геометрическую природу углов, их свойства и роль в различных математических конструкциях. Мы погрузимся в увлекательный мир углов и узнаем как они используются в разных сферах нашей жизни.
- Значение углов в геометрии.
- Свойства и особенности угловых фигур.
- Углы в архитектуре и дизайне.
- Углы в естественных феноменах.
- Применение углов в технике и строительстве.
Понимание геометрической интерпретации углов является ключевым для практического применения геометрии в различных областях жизни. Этот раздел позволит расширить наши познания о разнообразии углов и их значении в различных контекстах. Решение задач, связанных с углами, анализ геометрических фигур и способность видеть углы в повседневной жизни - все это может быть значимым преимуществом в разных сферах нашей деятельности.
Основные разновидности углов

В данном разделе мы рассмотрим различные классификации углов и их соответствующие характеристики. Мы изучим основные виды углов, которые встречаются в геометрии и имеют значительное практическое применение.
Первый вид углов, который мы рассмотрим, - это острые углы. Острые углы характеризуются меньшим значением меры угла, чем прямой угол, и они могут быть различных величин. Острые углы обычно встречаются в различных геометрических фигурах и играют важную роль при решении задач.
Второй вид углов - тупые углы. Тупые углы имеют меру больше, чем прямой угол, и они также могут варьироваться величиной. Тупые углы являются важным элементом при изучении теории углов и могут быть использованы для решения различных задач в геометрии и физике.
Третий вид углов - это прямые углы. Прямые углы имеют меру, равную 90 градусов, и являются основой для многих других угловых конструкций. Они используются в различных областях, включая архитектуру, инженерию и строительство.
Кроме того, мы рассмотрим специальные виды углов, такие как смежные углы, вертикальные углы и суплементарные углы. Эти углы играют важную роль в геометрических конструкциях и их характеристики могут быть использованы для решения различных задач.
Основные свойства и характеристики углов

В данном разделе мы рассмотрим основные свойства и характеристики, которыми обладают углы. Проясним их важность в различных сферах деятельности, где применяются геометрические концепции и понятия.
Углы являются одним из важнейших элементов геометрии, представляющими собой меру отклонения от прямой или плоской формы. Они используются не только в математике, но и в различных областях науки и практической деятельности.
Каждый угол имеет свои особенности, связанные с его величиной и положением в пространстве. Одним из главных свойств углов является их величина, которая может быть измерена в градусах, радианах или других единицах угловой меры.
Величина угла определяется также его отношением к окружности. Углы, составляющие 90 градусов, называют прямыми, а те, что больше 90 градусов - тупыми. Меньше 90 градусов - острые углы.
Одной из характеристик угла является его тип. Углы могут быть разносторонними, равнобедренными или равносторонними в зависимости от равенства или неравенства их сторон. Кроме того, углы классифицируются по своей закономерности и связанности с другими углами.
Понимание основных свойств и характеристик углов позволяет решать задачи по геометрии, строить формы и сооружения, а также применять их в науке и технике. Знание этих понятий необходимо для понимания многих принципов, связанных с изучением форм, механики и других областей человеческой деятельности.
| Величина | Типы углов | Характеристики |
|---|---|---|
| Малый, средний, большой | Прямой, тупой, острый | Разносторонний, равнобедренный, равносторонний |
Как измеряют углы:
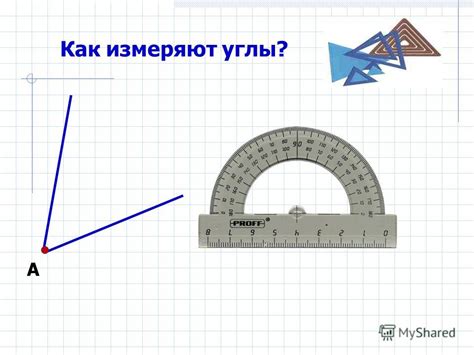
В данном разделе мы рассмотрим методы измерения углов без использования прямых определений фигур. Мы разберем, как оценить величину угла и узнать его значение, используя разные инструменты и техники.
- Измерение угла с помощью транспортира: величина угла определяется с помощью специального инструмента - транспортира. С его помощью можно точно измерить угол и определить его значение.
- Измерение угла с помощью гониометра: гониометр является более точным инструментом для измерения угла. Он имеет шкалу, которая позволяет определить величину угла с большей точностью.
- Определение величины угла с помощью секстанта: секстант - это инструмент, который используется в навигации для измерения углов между небесными объектами и горизонтом. С его помощью можно измерить угол с высокой точностью.
- Измерение угла с помощью тригонометрии: тригонометрия является математической дисциплиной, которая изучает связь между углами и сторонами треугольников. Используя тригонометрические функции, можно вычислить значение угла.
Это лишь некоторые из способов измерения углов, и каждый из них имеет свои преимущества в зависимости от ситуации и конкретной задачи. Независимо от выбранного метода, корректное измерение угла позволяет более точно работать с геометрическими фигурами, а также применять их результаты в различных областях, таких как архитектура, инженерия, физика и многие другие.
Роль углов в повседневной жизни: отражение измеряемых отношений

Взглянем на повседневные ситуации и задачи, где углы играют важную роль:
Архитектура и дизайн интерьера:
Углы помогают строителям и архитекторам создавать прочные и привлекательные построения. Они используются для определения наклона крыш, расположения стен, окон и дверей. Углы также помогают задавать гармоничные пропорции в интерьере, включая выбор мебели и размещение предметов.
Навигация:
В навигации углы используются для определения направления движения и ориентации. Компасы, GPS-навигаторы и карты базируются на использовании углов для указания пути и определения координат.
Измерения:
Углы помогают нам измерять и оценивать многие величины в повседневной жизни. Например, углы используются в строительстве для вычисления площадей и объемов, в механике для определения сил и напряжений, в фотографии и графике для создания перспективных иллюзий и т. д.
Порядок и структура:
Углы играют важную роль в упорядочении и структурировании информации. Например, в отраслях, связанных с управлением и организацией, углы используются для определения приоритетов, планирования и категоризации задач.
Таким образом, углы являются неотъемлемым элементом нашей повседневной жизни, обладают разнообразными свойствами и находят применение во многих областях, от строительства и навигации до измерений и структурирования информации.
Практическое использование углов:

- В архитектуре и инженерии углы применяются для определения расстояний между двумя точками, измерения площадей поверхностей, проектирования зданий и сооружений.
- В навигации и геодезии углы используются для определения направлений, углов наклона, а также для построения карт и планов местности.
- В изобразительном искусстве углы помогают создавать перспективу и гармоничные композиции, а также определять форму и пропорции объектов.
- В спорте углы играют важную роль при выполнении различных движений и техник, таких как футбольный удар, баскетбольное бросание или прыжки в прыжках в высоту.
- В тригонометрии углы широко используются для вычислений и определения связей между различными сторонами и углами треугольников.
Таким образом, знание и понимание углов является неотъемлемой частью не только математики, но и множества других дисциплин и практических задач. Важно уметь распознавать и измерять углы, а также применять их для решения различных задач в повседневной жизни и профессиональной деятельности.
Измерение углов с использованием специальных приборов

В данном разделе мы рассмотрим вопрос измерения углов и познакомимся с различными инструментами, которые позволяют удобно и точно определить величину угла.
Для определения угла, важного параметра в геометрии, существует несколько различных приборов. Одним из самых популярных и простых в использовании является угломер, или гониометр. Этот инструмент предоставляет возможность измерить угол между двумя прямыми или плоскостями с высокой точностью.
Другим распространенным инструментом для измерения углов является секстант. Он применяется в навигации и астрономии для определения высоты над горизонтом объектов, таких как звезды или маяки. С помощью секстанта можно определить угол между горизонтальной плоскостью и лучом света, отраженным от объекта.
Еще одним способом определения углов является использование универсального угломера. Этот инструмент позволяет измерять углы как по горизонтали, так и по вертикали, а также под разными углами относительно других линий или поверхностей.
Помимо специальных приборов, существуют также программные средства для измерения углов. Например, на компьютерах и смартфонах можно установить приложения, способные определять углы с использованием встроенных акселерометров и жестов пользователя.
Таким образом, измерение углов - это важный аспект как в науке и инженерии, так и в повседневной жизни. Различные инструменты и методы позволяют достичь высокой точности и надежности при определении углов и применении их в различных областях.
| Инструмент | Применение |
|---|---|
| Угломер | Строительство, изготовление мебели, геодезия |
| Секстант | Навигация, астрономия |
| Универсальный угломер | Точные измерения в различных отраслях |
| Программные средства | Помощь в решении задач геометрии и физики, инженерных расчетах |
Точные методы измерения углов:
В данном разделе рассматриваются методы, которые позволяют осуществлять точные измерения углов, являющихся важными характеристиками геометрических фигур. Прецизионные инструменты и приборы позволяют определить значения углов с высокой точностью, обеспечивая надежные результаты для различных областей применения.
Акклимационные приборы: эти приборы используются для измерения углов между отдельными объектами. Они позволяют точно определить угол, обеспечивая стабильные и точные значения на основе принципов оптики и геометрии.
Гониометры: это специальные измерительные инструменты, которые широко применяются для измерения углов в различных областях, таких как инженерия, архитектура, физика и астрономия. Гониометры обеспечивают высокую точность измерения и позволяют определить как внутренние, так и внешние углы.
Инклинометры: эти приборы используются для измерения углов наклона относительно горизонтальной или вертикальной оси. Они являются важным инструментом в геодезии, горно-добывающей промышленности и строительстве, где точные измерения наклона необходимы для обеспечения безопасности и оптимальной работы.
Интерферометры: эти измерительные приборы основаны на принципе интерференции света и применяются для точного измерения углов. Они часто используются в оптике и физике, а также в производстве и калибровке оптических компонентов.
Стерневые приборы: это астрономические инструменты, которые позволяют измерять углы между небесными объектами. Они используются в астрономии и навигации для определения положения небесных тел и ориентации в пространстве.
Использование этих точных методов измерения углов обеспечивает высокую точность и надежность в самых различных областях применения, где требуется точное определение углов для достижения оптимальных результатов.
Свойства углов и их взаимосвязь

Рассмотрим характеристики и особенности углов, а также их взаимосвязь между собой.
Когда мы говорим о свойствах углов, мы обращаем внимание на их размер, форму и положение. Каждый угол может иметь свою величину, выраженную в градусах, а также может быть остроугольным, прямым или тупоугольным.
Важным свойством углов является их сумма, которая может быть равной 180 градусам. Это наблюдается, например, в случае, когда прямая линия пересекает другую прямую и образует два угла - смежные углы. Их сумма всегда равна 180 градусам, независимо от их величины.
Кроме того, углы могут быть взаимно дополняющими или смежными. Взаимно дополняющие углы образуются, когда их сумма равна 180 градусам. Например, если один угол равен 45 градусам, то второй угол будет равен 135 градусам. Смежные углы, как уже упоминалось ранее, образуются при пересечении двух прямых линий и их сумма всегда равна 180 градусам.
Понимание свойств углов и их взаимосвязи является необходимым для решения различных задач, как в геометрии, так и во многих других областях, таких как архитектура, строительство и дизайн.
Основные свойства углов:
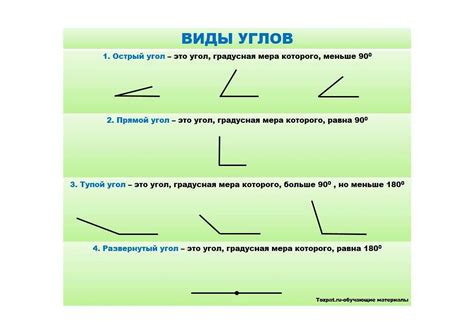
Существует несколько основных видов углов, включая острые углы, прямые углы, тупые углы и полные углы. Острые углы характеризуются меньшей мерой вращения между лучами и имеют значение менее 90 градусов. Прямые углы образуются при мере вращения в 90 градусов и имеют форму прямой. Тупые углы, напротив, имеют значение больше 90 градусов и характеризуются более широким отклонением лучей. Полные углы имеют меру вращения 360 градусов и представляют собой полную окружность.
Основные свойства углов включают их суммы, различные формулы для вычисления значений углов, а также использование углов в различных областях, таких как геометрия, физика, архитектура и дизайн. Углы используются для измерения поворотов и направлений, а также как важный инструмент в построении и расчетах различных конструкций.
| Тип угла | Характеристики | Применение |
|---|---|---|
| Острый угол | Меньше 90 градусов | Измерение угловой меры, геометрические конструкции |
| Прямой угол | 90 градусов | Перпендикулярные линии, прямые углы в геометрии |
| Тупой угол | Больше 90 градусов | Углы наклона, геометрические проблемы, повороты |
| Полный угол | 360 градусов | Круговые диаграммы, географические ориентации |
Знание основных свойств углов является важным для понимания пространственных отношений и применений углов в различных практических областях.
Пересечение прямых и формирование углов
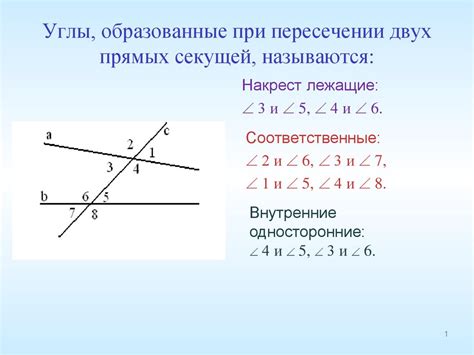
Пересечение двух прямых формирует углы, которые могут быть как острыми, так и тупыми. Острый угол означает, что две прямые пересекаются и образуют угол меньше 90 градусов. Тупой угол, наоборот, означает, что две прямые пересекаются и образуют угол больше 90 градусов. Кроме того, существуют и другие виды углов, такие как прямой угол, который равен 90 градусам, и полный угол, который составляет 180 градусов. Все эти углы имеют свои особенности и характеристики, которые играют важную роль в геометрии.
- Острые углы являются привычными для нас, так как они часто встречаются в ежедневной жизни. Эти углы используются в архитектуре для создания красивых и эстетических форм зданий, в дизайне для размещения элементов интерьера и в различных конструкциях.
- Тупые углы находят применение в различных областях, например, в телекоммуникациях для определения направления сигнала или в строительстве для определения ориентации объектов относительно друг друга.
- Прямые углы являются одними из самых важных углов в геометрии, поскольку они широко применяются в построении перпендикулярных линий и поверхностей, а также в оптике для отражения и преломления света.
- Полные углы играют важную роль в изучении окружности и ее свойств, а также в компьютерной графике для реализации различных алгоритмов визуализации.
В целом, понимание того, как пересекаются прямые и образуются углы, является фундаментальным для изучения геометрии и находит широкое применение в различных областях науки и техники. Знание основных типов углов, их характеристик и возможностей помогает нам анализировать и визуализировать сложные геометрические объекты, а также применять их для решения задач в реальном мире.
Вопрос-ответ

Какую роль играют углы в геометрии?
Углы являются основными элементами геометрии и они имеют важное значение для изучения фигур и объектов. Они позволяют определить форму фигур, измерять их размеры и проводить различные расчеты. Углы помогают определить направление, ориентацию и расположение объектов в пространстве.
Какие основные виды углов существуют?
Существует несколько основных видов углов, включая прямой угол, острый угол и тупой угол. Прямой угол составляет 90 градусов и является прямой линией, разделяющей плоскость на две одинаковые части. Острый угол составляет меньше 90 градусов и имеет острые концы. Тупой угол составляет больше 90 градусов и имеет тупые концы.
Для чего нужно изучать углы и какие практические применения они имеют?
Изучение углов имеет практическое применение во многих областях науки и техники. Например, архитекторы и строители используют углы для создания и расчета конструкций зданий. Углы также используются в навигации и геодезии для определения направления и прокладки маршрутов. Медицинские специалисты могут использовать углы для анализа рентгеновских снимков и диагностики заболеваний. Кроме того, углы являются важными элементами в изучении физики, математики и технических наук.



