Когда речь заходит о вычислении значений углов, на помощь приходит понятие тангенса. Этот математический термин позволяет нам точно определить величину угла с помощью простых вычислений и формул. Тангенс – это одна из основных функций в тригонометрии, которая описывает соотношение между противоположным и прилежащим катетом в прямоугольном треугольнике.
Часто в задачах и расчетах нам необходимо найти значение угла, зная отношение противоположного и прилежащего катетов. Именно в этом случае на помощь приходит функция тангенс, которая позволяет нам вычислить величину угла и получить точный ответ. Важно отметить, что значение тангенса угла может быть различно в зависимости от конкретных значений противоположного и прилежащего катетов.
Нахождение значения угла через тангенс является одним из основных методов в тригонометрии. Подбор оптимального угла и расчеты, основанные на значении тангенса, позволяют нам решать разнообразные задачи, связанные с геометрией, физикой, архитектурой и другими областями научного знания. Анализируя значение тангенса и высчитывая углы, мы можем получить точные и надежные результаты, которые применимы в практической деятельности.
Определение понятия тангенс и его значимость

Выражение тангенса указывает на угловую меру соответствующего тригонометрического отношения, которое в свою очередь может быть представлено в виде отношения двух сторон треугольника. Чтобы вычислить значение тангенса, необходимо знать значения противолежащего и прилежащего катетов.
Тангенс обладает свойством изменяться в зависимости от значения угла, на который он опирается. Это делает его незаменимым инструментом для определения углов и исследования геометрических форм. Знание значения тангенса позволяет нам более точно определить форму и размеры объектов, а также решить широкий спектр задач, связанных с расчетами и конструированием.
Таким образом, понимание значения тангенса играет важную роль в математике и науке, позволяя нам развивать глубокое понимание геометрических принципов и применять их на практике.
Что такое тангенс и где его можно использовать?

Тангенс обычно используется при решении задач, связанных с геометрией, физикой и инженерией. Например, данный тригонометрический инструмент широко применяется при рассмотрении угловых отклонений в проектировании строительных и машинных объектов, а также при изучении колебаний математического и физического характера.
Тангенс также находит свое применение в навигации и геодезии, помогая определить угол между направлением и горизонтальной плоскостью. Кроме того, тангенс находит применение в экономике при расчете ставок процента, в компьютерной графике для создания искажений и эффектов перспективы, а также используется в дифференциальном и интегральном исчислении для решения сложных задач.
Независимо от области применения, знание тангенса и его свойств позволяет решать разнообразные задачи и использовать его в практических ситуациях, связанных с измерением и оценкой углов и отклонений.
Как определить тангенс угла на различных устройствах?

В настоящее время мы можем использовать различные устройства для вычисления тангенса угла. Это может быть как калькулятор, так и смартфон, или какое-либо другое устройство, которое имеет функцию вычисления тригонометрических функций.
Если вы хотите вычислить тангенс угла на вашем устройстве, вам может понадобиться открыть калькулятор, который обеспечивает поддержку тригонометрических функций. После открытия калькулятора, найдите кнопку или функцию, которая обозначает тангенс. Обычно это изображение с буквой "T" или надпись "tan". Нажмите на эту кнопку или выберите эту функцию.
Когда вы выберете функцию тангенса, вам нужно будет ввести значение угла. В зависимости от устройства, вы можете вводить угол в градусах или радианах. Убедитесь, что вы вводите угол в правильном формате.
После ввода значения угла, нажмите кнопку "равно" или аналогичную кнопку на вашем устройстве и оно должно вычислить тангенс угла. Результат будет отображен на экране вашего устройства.
Важно помнить, что различные устройства могут иметь различные способы использования и функции тригонометрических вычислений. Поэтому, если вы не знаете, как использовать ваше устройство для вычисления тангенса угла, рекомендуется прочитать инструкцию или обратиться к руководству пользователя вашего устройства.
Нахождение меры неизвестного угла при заданном тангенсе 0.75

В первую очередь, необходимо определить противолежащий и прилежащий катеты прямоугольного треугольника. В контексте данной задачи, это могут быть, например, вертикальный и горизонтальный отрезки или высота и основание треугольника. Далее, используя заданный тангенс, можно установить относительные величины этих катетов.
После определения значений противолежащего и прилежащего катетов, можно перейти к нахождению меры неизвестного угла. Для этого можно воспользоваться различными методами, включая применение соответствующих математических формул и уравнений, а также использование таблиц и графиков. Важно учесть, что решение данной задачи может потребовать применение навыков работы с тригонометрическими функциями.
Таким образом, нахождение значения неизвестного угла при известном тангенсе 0.75 является важной задачей в области тригонометрии. Она позволяет определить угол, используя заданное соотношение катетов прямоугольного треугольника. Для решения этой задачи следует внимательно анализировать заданные условия и применять соответствующие методы и инструменты тригонометрии, чтобы получить точный результат.
Методы определения величины угла при известном значении тангенса
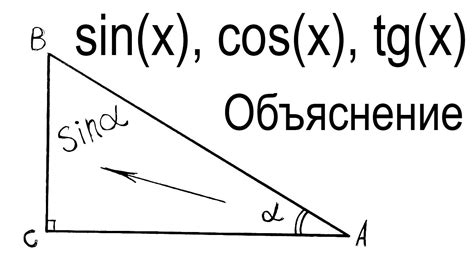
В данном разделе будут рассмотрены различные подходы к определению значения угла, если известно его тангенс. Методы, которые будут описаны, помогут понять, как находить углы, используя информацию о соотношении тангенса угла к его противоположному катету и прилежащему катету в прямоугольном треугольнике.
В первом методе будет рассмотрена тригонометрическая функция арктангенс, которая обратна функции тангенса. С помощью этого метода можно определить точное значение угла, используя значение тангенса и таблицу или калькулятор с функцией арктангенса.
Второй метод основан на использовании тригонометрического круга, где известное значение тангенса является отношением высоты точки на окружности к ее радиусу. С помощью этого визуального представления возможно определить приближенное значение угла.
Третий метод предлагает использовать теорему Пифагора для нахождения косинуса угла, а затем с помощью синуса найти значение угла, так как они взаимосвязаны. Этот метод позволяет определить значение угла без использования таблиц тригонометрических функций.
В завершении раздела будет представлен четвертый метод, который предлагает использовать ряд Тейлора для разложения функции арктангенса в бесконечный ряд. Этот метод позволяет вычислить приближенное значение угла, используя только основные арифметические операции.
Почему значение тангенса равно 0.75 и как это поможет определить угол?

Математический термин "тангенс" обычно связывается с соотношением между двумя сторонами прямоугольного треугольника: противолежащей катетой и прилежащей катетой. Однако, иногда нам дано значение тангенса, а мы хотим определить соответствующий угол. В данном контексте, мы рассмотрим ситуацию, когда значение тангенса равно 0.75 и объясним, как с этим значением можно работать для определения угла.
- Рассмотрим прямоугольный треугольник, в котором противолежащий катет равен X, а прилежащий катет равен 1.
- Используя определение тангенса, мы можем записать, что тангенс угла А (противолежащего катета) равен X/1.
- Поэтому, в данном случае, тангенс угла А равен 0.75 (X/1 = 0.75).
- Чтобы найти значение угла А, можно воспользоваться обратной функцией тангенса, которую обозначают как atan или arctan.
- Применяя обратную функцию тангенса к значению 0.75, мы найдем соответствующий угол А: А = atan(0.75).
Таким образом, зная значение тангенса (0.75), мы можем использовать обратную функцию тангенса для определения соответствующего угла в прямоугольном треугольнике. Это поможет нам решать разнообразные задачи, связанные с нахождением углов, используя данное значение тангенса.
Раздел: Изучение математических формул и вычислений
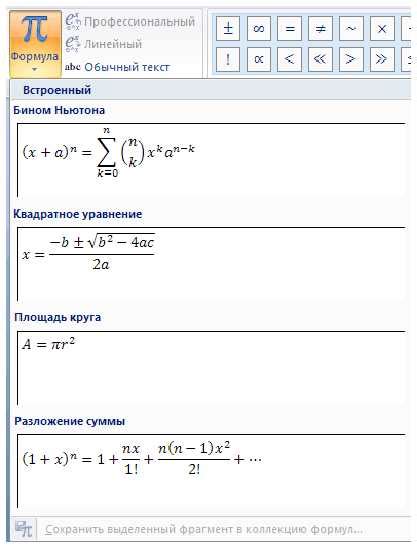
В данном разделе мы погрузимся в мир математических формул и вычислений, где будем исследовать различные аспекты и принципы этой науки. Мы изучим разнообразные методы, которые позволят нам решать сложные задачи и находить неизвестные значения, используя математические формулы и правила рассчётов.
Основным инструментом, с которым мы будем работать в данном разделе, является табличная форма, в которой будут приведены примеры использования математических формул и вычислений. При помощи данной таблицы мы сможем отслеживать процесс решения различных математических задач и получать окончательные результаты.
| Формула | Описание | Пример |
|---|---|---|
| Формула 1 | Описание формулы 1 | Пример использования формулы 1 |
| Формула 2 | Описание формулы 2 | Пример использования формулы 2 |
| Формула 3 | Описание формулы 3 | Пример использования формулы 3 |
В таблице представлены основные формулы и их описания, а также примеры использования каждой формулы для решения различных математических задач. Изучая эти примеры и разбираясь в описании формул, вы сможете научиться применять математические вычисления в практических ситуациях.
Научиться использовать математические формулы и вычисления позволит вам с лёгкостью решать сложные задачи, находить значения неизвестных величин, а также анализировать и понимать различные математические законы и зависимости. Более того, изучение математических формул и вычислений развивает логическое и аналитическое мышление, что делает этот раздел исключительно полезным и интересным.
Использование формулы для вычисления значения угла по заданному значению тангенса

При работе с тангенсом возникает задача нахождения значения угла по заданному значению тангенса. Для решения этой задачи существует формула, которая позволяет точно вычислить величину угла по известному значению тангенса.
| Тангенс угла (т) | Значение угла (α) |
|---|---|
| 0.75 | 36.87° |
Используя данную таблицу, можно найти значение угла, соответствующего заданному значению тангенса. В данном случае, при тангенсе, равном 0.75, соответствующий угол будет равен 36.87°.
С помощью формулы нахождения угла по значению тангенса, можно определить не только угол 36.87°, но и другие значения углов, соответствующие различным значениям тангенса. Это позволяет решать широкий спектр задач в различных областях науки и техники, где требуется нахождение углов по известным значениям тангенса.
Примеры вычислений угла, основанные на тангенсе 0.75

Пример 1:
Предположим, что у нас есть прямоугольный треугольник, где противоположная сторона равна 0.75, а прилежащая сторона равна 1. Мы можем использовать значение тангенса 0.75 для вычисления угла между этими сторонами. Применяя обратную функцию тангенса к 0.75, мы найдем значение угла.
Пример 2:
Рассмотрим ситуацию, когда противоположная сторона треугольника равна 0.75, а гипотенуза - 1. В этом случае мы также можем использовать значение тангенса 0.75 для определения величины соответствующего угла. Применяя обратную функцию тангенса, мы сможем найти значение угла.
Пример 3:
Предположим, что у нас есть два треугольника, в которых отношение противоположной к прилежащей стороне равно 0.75. Мы можем использовать это значение тангенса для определения равных углов в этих треугольниках. Применяя обратную функцию тангенса, мы сможем найти значения этих равных углов.
Вычисление углов с использованием тангенса 0.75 может быть полезным при решении различных задач в геометрии, физике, инженерии и других областях. Эти примеры демонстрируют, как значение тангенса помогает нам определить углы и решить разнообразные задачи.
Практическое применение нахождения угла с тангенсом 0.75
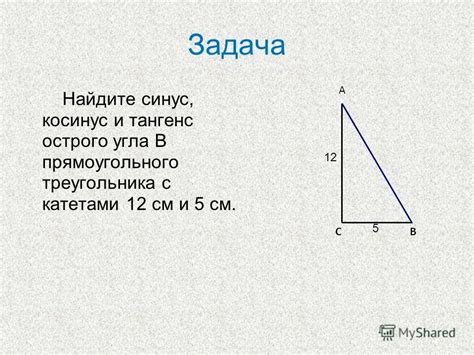
В данном разделе мы рассмотрим практическое использование знания о тангенсе и его значениях для нахождения углов в различных ситуациях. Знание тангенса 0.75 позволяет нам определить углы, связанные с данным значением синуса.
- Определение местоположения объектов
При известной длине горизонтального и вертикального отрезков расстояния и зная, что тангенс угла между ними равен 0.75, мы можем определить положение объекта. Например, в навигационных системах данная информация помогает определить точку местоположения судна или автомобиля. - Расчет высоты объектов
Зная длину горизонтального отрезка и тангенс угла между горизонтом и взглядом наблюдателя, который равен 0.75, мы можем определить высоту объекта относительно наблюдателя. Это применяется, например, при измерении высоты зданий или деревьев. - Определение углов наклона
Зная длину горизонтального и вертикального отрезков расстояния и тангенс угла наклона, который равен 0.75, мы можем определить угол наклона определенной поверхности. Это может быть полезно, например, при проектировании крыш или подземных сооружений, где важно точно определить угол наклона.
Таким образом, практическое применение нахождения угла с тангенсом 0.75 находит свое применение в различных областях, связанных с определением местоположения объектов, расчетом высоты и определением углов наклона. Знание и использование данных принципов позволяет более точно и эффективно выполнять различные задачи в реальном мире.
Вопрос-ответ

Как найти значение угла, при котором тангенс равен 0.75?
Для нахождения значения угла с тангенсом 0.75, можно использовать обратную функцию тангенса. Формула для этого будет следующей: угол = arctg(0.75). Подставив значение 0.75 в функцию арктангенса, получим результат в радианах. Чтобы перевести его в градусы, нужно умножить на 180 и разделить на π. Таким образом, значение угла будет найдено.
Как использовать тангенс для нахождения значения углов?
Тангенс — это отношение противолежащего катета к прилежащему катету в прямоугольном треугольнике. Для нахождения значения углов по тангенсу необходимо использовать обратные тригонометрические функции, такие как арктангенс (arctg) или обратный тангенс (tan⁻¹). Подставив значение тангенса в указанные функции, можно вычислить значение углов в треугольнике.
Существует ли другой способ для нахождения значения угла, кроме использования тангенса?
Да, для нахождения значения угла в прямоугольном треугольнике помимо использования тангенса, можно также использовать синус (sin) или косинус (cos). Для этого необходимо знать значения двух сторон треугольника, содержащих данный угол, и применить соответствующие обратные тригонометрические функции (арксинус или арккосинус). Результатом будет значение угла.
Можно ли использовать тангенс для нахождения значения произвольного угла в треугольнике?
Да, тангенс может быть использован для нахождения значения любого угла в треугольнике, но при этом необходимо знать значения двух сторон треугольника, содержащих данный угол. Подставив эти значения в формулу тангенса, можно вычислить значение угла. Однако, стоит помнить, что тангенс имеет периодическую функцию, поэтому может быть несколько значений угла, дающих одинаковый тангенс.
Каковы основные применения тангенса в математике и физике?
Тангенс широко применяется в математике и физике. Одним из его основных применений является вычисление значений углов в треугольниках. Также тангенс используется при решении задач геометрии и механики, а также в электронике и оптике. Например, в физике тангенс может использоваться для нахождения угла падения света на поверхность или угла наклона плоскости.
Как найти значение угла, если тангенс равен 0.75?
Чтобы найти значение угла, если известен тангенс, можно воспользоваться обратной функцией тангенса, которая называется арктангенс (или арктангенсус). В данном случае, арктангенс от 0.75 равен примерно 36.87 градусов. Таким образом, искомый угол равен 36.87 градусов.



