Когда сталкиваешься с задачей восстановления окружности, зная только одну из ее хорд, это может показаться сложным и запутанным. Однако, с помощью геометрического алгоритма, вы сможете легко и точно определить положение окружности.
Весь процесс состоит из последовательных шагов, которые позволяют найти центр и радиус окружности, используя только известную хорду. При этом не требуется знание дополнительных параметров или точек, что делает алгоритм универсальным и применимым для различных случаев.
Суть геометрического алгоритма заключается в использовании свойств окружности и ее хорды. Отрезок называется хордой, когда оба его конца лежат на окружности. На основе этого свойства и основных формул геометрии, можно получить точное решение задачи.
Основные понятия: окружность и хорда
Окружность представляет собой геометрическую фигуру, которая состоит из всех точек в плоскости, равноудаленных от фиксированной точки, называемой центром окружности. Эта фигура обладает рядом особенностей, таких как равенство всех радиусов, которые соединяют центр с точками окружности.
Хорда – это отрезок, который соединяет две точки на окружности. Отличительной особенностью хорды является то, что она лежит внутри окружности и ее концы лежат на самой окружности. Можно сказать, что хорда является одной из основных составляющих окружности и определяет ее свойства и размеры.
Имея представление об этих понятиях, мы можем перейти к более детальному рассмотрению методов нахождения окружности по известной хорде, что позволит нам более точно определить ее радиус и центр.
Математические свойства окружности и ее отношение к хорде

Одно из основных свойств окружности и хорды заключается в том, что диаметр окружности является наибольшей хордой. Диаметр проходит через центр окружности и делит его на две равные части. Поэтому любая хорда окружности никогда не может быть длиннее диаметра. Важно отметить, что диаметр окружности является самой короткой хордой, так как соединяет две точки на окружности, находящиеся на краю фигуры.
Другое важное математическое свойство окружности и хорды связано с центральным углом, образуемым хордой и радиусом, проведенным из центра окружности к точке пересечения хорды с окружностью. Закономерность заключается в следующем: центральный угол, опирающийся на хорду, равен удвоенному углу, опирающемуся на дугу между концами хорды. Таким образом, можно использовать данное свойство для вычисления неизвестных углов, основываясь на известных дугах или хордах в окружности.
Таким образом, изучение математических свойств окружности и хорды позволяет нам получить глубокое понимание их взаимосвязи и использовать эти знания в решении различных задач. Эти свойства являются фундаментальными для изучения геометрии и математического анализа, а также находят применение в различных технических и научных областях.
Расчет радиуса окружности с применением хорды: основные шаги
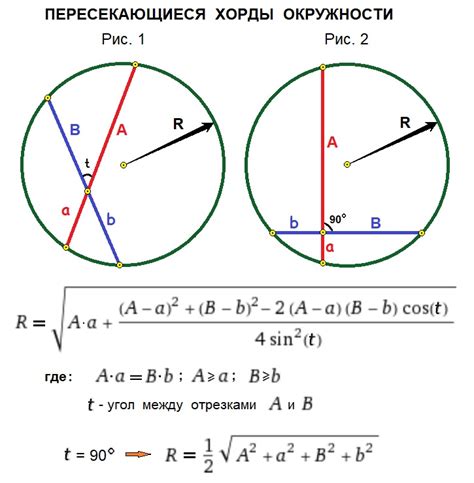
В этом разделе будут представлены ключевые шаги и формула для определения радиуса окружности, исходя из заданной хорды. Мы рассмотрим суть процесса без углубления в конкретные математические определения.
Шаг 1: Измерьте длину хорды
Первым шагом является измерение длины хорды. Для точности результата необходимо использовать точные измерительные инструменты.
Шаг 2: Найдите середину хорды
Далее, определите середину хорды. Для этого разделите длину хорды пополам, используя полученные измерения.
Шаг 3: Определите расстояние от середины хорды до центра окружности
Для нахождения радиуса необходимо определить расстояние от середины хорды до центра окружности. Это и будет радиусом искомой окружности.
Шаг 4: Примените формулу для нахождения радиуса
Наконец, используя значения длины хорды и расстояния от середины хорды до центра окружности, можно применить формулу для определения радиуса окружности.
Это основная последовательность действий, которую следует выполнить для нахождения радиуса окружности при известной хорде. Обратите внимание, что этот метод основан на простых математических принципах и является эффективным способом решения данной задачи.
Шаги для определения радиуса окружности по известному участку
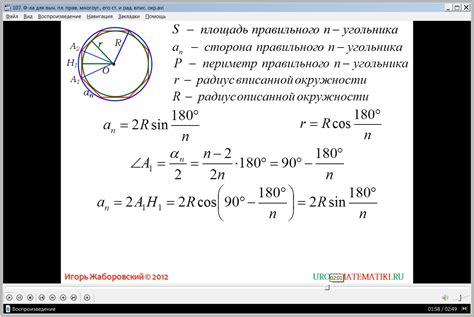
В данном разделе мы рассмотрим пошаговую инструкцию по нахождению значения радиуса окружности, если известен участок дуги, который она охватывает. Для этого воспользуемся методом, основанным на синусе, арксинусе и формуле половинного угла.
1. Вычислите значение половинного угла, по которому простирается заданный участок дуги окружности. Для этого используется формула: половинный угол = угол дуги / 2. Здесь угол дуги выражается в радианах.
2. Далее найдите значение синуса половинного угла, применяя формулу: sin(половинный угол) = длина хорды / (2 * радиус окружности).
3. С помощью найденного значения синуса половинного угла, определите значение радиуса окружности по формуле: радиус окружности = длина хорды / (2 * sin(половинный угол)).
В итоге, применяя указанные шаги, вы сможете точно определить радиус окружности, имея информацию только о длине хорды и угле, который она охватывает. Учтите, что в данной методике мы предполагаем, что хорда не делит окружность на равные части, иначе она будет являться диаметром окружности.
Решение задач с последовательным объяснением

В этом разделе мы предлагаем вам решить несколько примеров, связанных с определением окружности по известной хорде. Мы пошагово объясним каждый шаг решения, чтобы помочь вам лучше понять процесс и самостоятельно повторить его в будущем. Каждый пример будет сопровождаться подробными пояснениями, а также некоторыми полезными синонимами, чтобы разнообразить текст и улучшить вашу языковую подготовку.
- Шаг 1: Анализ условия задачи
- Шаг 2: Работа с известными данными
- Шаг 3: Применение соответствующих формул или методов
- Шаг 4: Проверка и аргументация результата
Перед тем как приступить к решению, важно внимательно прочитать условие задачи и понять, что от нас требуется. Возможно, нам потребуется определить длину хорды, узнать радиус окружности или найти координаты ее центра. Такой анализ поможет нам определить стратегию решения и выбрать подходящие математические методы или формулы.
После того как мы понимаем, что нам нужно решить, следующий шаг - работа с известными данными. Нам могут быть даны координаты концов хорды, угол, под которым она пересекает окружность или другая информация. Здесь мы будем использовать синонимы для разнообразия текста, такие как "дано", "предоставлено" или "имеем". Мы также объясним, какие данные нам важны для дальнейшего решения задачи.
На этом этапе мы будем использовать подходящие формулы и методы, чтобы вычислить неизвестные величины. Здесь возможно использование слов и выражений, связанных с вычислением, определением или нахождением. Мы пошагово объясним процесс применения формул и дадим необходимые пояснения, чтобы вы могли легко повторить это в будущем.
В конце решения задачи важно проверить полученные результаты и аргументировать их. Мы объясним, как проверить наши вычисления с помощью геометрических свойств окружностей и хорд. Мы также опишем способы аргументации результатов, используя выражения типа "следовательно", "в итоге" или "поэтому".
Практическое применение формулы для нахождения окружности
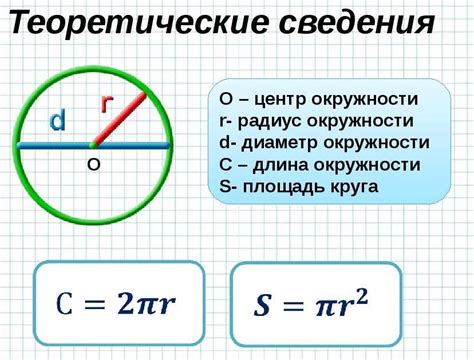
В данном разделе мы рассмотрим реальные ситуации, в которых формула нахождения окружности может быть полезной. Благодаря этой формуле вы сможете определить радиус и центр окружности, что поможет вам во многих практических задачах.
Например, представим, что у вас есть фруктовый сад. Вы желаете поставить ограду вокруг его границы. Вам известно, что диаметр окружности, ограждающей весь сад, равен 20 метрам. С помощью нашей формулы вы сможете вычислить радиус данной окружности, что поможет вам подобрать правильный материал для ограды и рассчитать его количество.
Кроме этого, формула нахождения окружности имеет широкое применение в строительстве. Например, вам необходимо установить круглую крышу на строение определенного диаметра. С использованием предложенной формулы вы сможете определить радиус окружности, исходя из которого будете знать, какой диаметр должна иметь крыша, чтобы идеально уложиться в заданные размеры.
В мире географии также существует практическое применение формулы нахождения окружности. Например, при определении площади страны или водоема можно использовать радиус окружности и формулу для вычисления. Это поможет в проведении географических исследований и составлении карт, а также в планировании транспортных маршрутов и определении границ регионов.
- Практическое использование формулы нахождения окружности в фруктовом саду;
- Применение формулы в строительстве для определения размеров крыши;
- Географическое применение формулы при определении площади стран и водоемов.
Резюме и полезные советы при работе с окружностями и хордами
Этот раздел представляет собой конденсацию информации и дает полезные советы по работе с окружностями и хордами. Здесь вы найдете основные принципы, рекомендации и разнообразные подходы, которые пригодятся вам при изучении данной темы.
- Исследуйте свойства окружности - продолжайте изучать различные характеристики окружности, такие как радиус, диаметр, длина окружности и т.д.
- Определите основные понятия - изучите основные термины, связанные с окружностями и хордами, такие как дуга, сектор, центральный угол и т.д. Это поможет вам лучше понять связи между ними.
- Изучите теоремы - ознакомьтесь с теоремами, связанными с хордами и окружностями, и разберитесь, как их применять для нахождения неизвестных величин.
- Примените геометрические основы - используйте базовые геометрические принципы, чтобы найти связь между хордами и окружностями, опираясь на предоставленные данные.
- Практикуйтесь - чтобы лучше понять материал и освоить его, решайте разнообразные задачи, связанные с хордами и окружностями. Это поможет закрепить полученные знания и навыки.
Запомните, что успешное решение задач по нахождению окружности по известной хорде требует тщательного анализа и применения усвоенных принципов. Работа с хордами и окружностями может быть увлекательным и познавательным опытом, который будет полезен вам как в академической среде, так и в повседневной жизни.
Вопрос-ответ

Как найти окружность по известной хорде?
Для того, чтобы найти окружность по известной хорде, необходимо знать еще одну величину – высоту треугольника, образованного хордой и радиусом окружности. Формула для вычисления радиуса окружности в данном случае выглядит следующим образом: r = (h² + c²) / (2h), где r – радиус окружности, h – высота треугольника, а c – известная хорда.
Какой метод использовать при нахождении окружности по известной хорде?
При нахождении окружности по известной хорде используется метод, основанный на нахождении высоты треугольника, образованного хордой и радиусом окружности. По формуле r = (h² + c²) / (2h) можно вычислить радиус окружности.
Как определить высоту треугольника по известной хорде?
Для определения высоты треугольника по известной хорде необходимо использовать теорему Пифагора. Если c – известная хорда, а r – радиус окружности, то высоту треугольника можно вычислить по формуле h = √(r² - c²).
Какие данные нужны, чтобы найти окружность по известной хорде?
Для того, чтобы найти окружность по известной хорде, необходимо знать измерения хорды и радиуса окружности. Также важно знать геометрические свойства окружности, а именно, что хорда является отрезком, соединяющим две точки на окружности.
Есть ли другие методы нахождения окружности по известной хорде?
Да, помимо метода нахождения окружности по известной хорде с использованием высоты треугольника, существуют и другие методы. Например, можно использовать метод, основанный на определении центра окружности по трём точкам, лежащим на хорде. Этот метод требует большего количества данных, но может быть использован в случаях, когда высота треугольника неизвестна.
Как найти центр окружности, если известна только её хорда?
Если известна длина хорды, то для нахождения центра окружности требуется знать еще одну точку окружности, кроме концов хорды. Эта точка может быть задана координатами или вектором.
Как вычислить радиус окружности, если известна только её хорда?
Для вычисления радиуса окружности по известной хорде необходимо знать либо длину хорды и расстояние от центра окружности до хорды, либо угол, который хорда образует с диаметром, проходящим через её концы.



