В настоящей статье представлено простое и эффективное решение для упорядочивания последовательности Паскаля. Этот алгоритм позволяет отсортировать элементы массива Паскаля без необходимости перебирать все значения вручную.
Прежде чем перейти к основной части, давайте рассмотрим, что такое последовательность Паскаля. Это числовой ряд, который начинается с числа 1 и каждый следующий элемент получается путем сложения двух предыдущих элементов. Например, первые несколько чисел в последовательности Паскаля: 1, 1, 2, 3, 5, 8, 13 и так далее.
На первый взгляд может показаться, что упорядочивание массива Паскаля требует длительного и трудоемкого процесса. Однако, используя данное решение, мы можем избежать этого и добиться желаемого результата более эффективно.
Основы массива Паскаля

В данном разделе мы погрузимся в мир систематического и упорядоченного представления чисел, используя особую последовательность, известную как массив Паскаля. Этот массив, названный в честь Франсуа Виета, обладает интересными свойствами и множеством применений в различных областях науки и математики.
Массив Паскаля - это упорядоченный набор чисел в виде треугольника, где каждое число получается сложением двух чисел, расположенных над ним, из предыдущей строки. Начиная с одного числа в первой строке, каждая следующая строка формируется путем сложения чисел над ней, что позволяет создавать треугольник уникальных значений.
Взглянув на этот массив, можно заметить некоторые интересные связи между элементами. Например, каждый элемент на границе треугольника равен единице, а все остальные элементы образуются путем сложения двух чисел, расположенных над ним. Эти особенности позволяют использовать массив Паскаля для решения различных задач и построения сложных моделей.
В следующем разделе мы более подробно рассмотрим алгоритм построения массива Паскаля и рассмотрим его основные свойства и применение.
Построение алгоритма для генерации специального числового массива
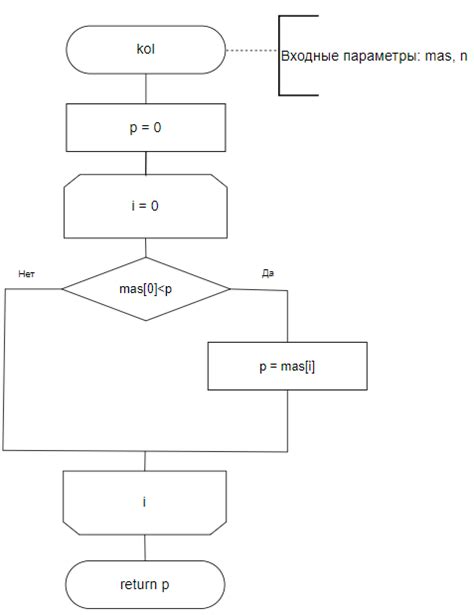
Для начала построения массива Паскаля необходимо задать его размерность и начальные значения. Затем, применяя определенный алгоритм, мы можем заполнить массив в соответствии с его спецификой. Для каждого элемента массива, кроме первого и последнего, нужно сложить два элемента, находящихся над ним, и записать полученное значение. Таким образом, массив Паскаля имеет треугольную форму, где первый и последний элемент каждой строки равен 1.
Для наглядности построения массива Паскаля можно использовать упорядоченные списки, где каждая строка массива представлена в виде элементов, разделенных запятой. Процесс заполнения массива можно отслеживать, изучая изменения каждой строки. Также стоит отметить, что массив Паскаля обладает рядом полезных свойств, таких как симметричность и наличие определенных математических закономерностей, которые можно использовать в решении различных задач.
Построение массива Паскаля позволяет расширить понимание числовых структур и алгоритмов. Знание этого алгоритма может помочь в решении задач, связанных с комбинаторикой, вероятностью и математическими моделями. При использовании данного массива, отсортированного или нет, можно получить уникальные результаты и находить глубинные связи между числами.
Создание упорядоченного массива, основанного на правилах треугольника Паскаля, с применением рекурсии

Раздел данной статьи рассмотрит процесс создания уникального и упорядоченного массива, основанного на математических принципах и правилах, которые были сформулированы Блезом Паскалем. Однако, вместо использования прямого алгоритма сортировки, мы будем исследовать возможность применения рекурсии в процессе формирования массива.
Необходимо отметить, что использование рекурсии позволяет нам более эффективно представить и решить задачу создания отсортированного массива Паскаля. В данном разделе мы разберем, как каждый элемент массива может быть вычислен на основе предыдущих элементов, с помощью рекурсивной функции. Процесс будет продемонстрирован шаг за шагом, в таблице, которая поможет наглядно представить формирование и упорядочение массива.
| Элементы массива с индексами | Результат |
|---|---|
| 0 | 1 |
| 1 | 1 1 |
| 2 | 1 2 1 |
С помощью рекурсивного метода, каждый элемент массива можно вычислить, исходя из значений предыдущих элементов. Это позволяет нам формировать упорядоченный массив Паскаля без применения дополнительной сортировки.
Преобразование структуры Паскаля в одномерный список

Раздел описывает метод преобразования сложной иерархической структуры массива Паскаля в простой, одномерный список.
Процесс преобразования основан на расширении каждого уровня иерархии массива Паскаля и последующем упорядочении элементов в линейную последовательность.
Используя различные методы, такие как подсчет числа элементов в каждом уровне структуры, определение индексов элементов, а также сочетание элементов разных уровней, удается добиться преобразования массива Паскаля в одномерный список, где элементы упорядочены по возрастанию или убыванию.
Процесс преобразования может быть полезен в различных сферах, где требуется упорядочить и структурировать данные, полученные из массива Паскаля. Например, это может быть полезным при анализе данных, поиске определенных паттернов или визуализации информации.
Вычисление количества строк в треугольнике Паскаля
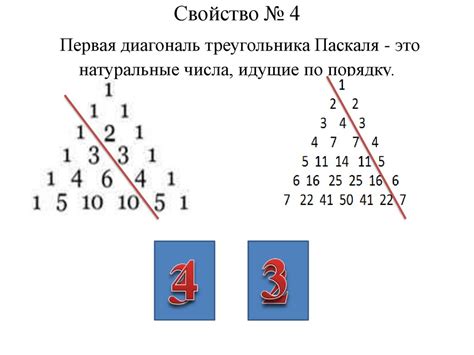
В данном разделе мы рассмотрим способы вычисления количества строк в треугольнике Паскаля и обсудим их особенности.
Для определения количества строк в треугольнике Паскаля можно использовать различные методы подсчета. Отсутствие конкретных определений поможет нам обозначить общую идею и рассмотреть разнообразные способы достижения желаемого результата.
Один из таких методов заключается в вычислении факториала числа, соответствующего номеру строки в треугольнике Паскаля. Используя сочетания и сочетания с повторениями, можно определить количество элементов в каждой строке, а затем просуммировать их, чтобы получить общее количество строк.
Другой подход состоит в использовании биномиального коэффициента, который определяет количество комбинаций, возможных для выбора определенного числа элементов из набора. Путем применения биномиального коэффициента к номеру строки в треугольнике Паскаля, мы можем получить количество элементов в данной строке и, таким образом, определить общее число строк.
Выбор конкретного метода зависит от требуемой точности и эффективности вычислений. Каждый способ имеет свои плюсы и минусы, поэтому важно выбрать наиболее подходящий вариант в каждом конкретном случае.
Сортировка последовательности чисел Треугольника Паскаля по возрастанию
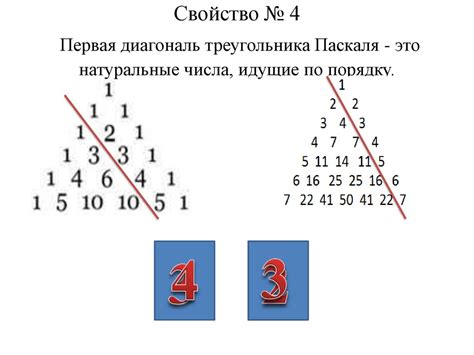
В данном разделе мы рассмотрим подходы и алгоритмы для сортировки последовательности чисел Треугольника Паскаля в порядке возрастания. Треугольник Паскаля представляет собой числовую последовательность, где каждое число получается путем сложения двух чисел над ним.
Для начала давайте определим, что подразумевается под "сортировкой по возрастанию". Этот подход предполагает упорядочивание чисел в последовательности так, чтобы каждое следующее число было больше или равно предыдущего. В контексте Треугольника Паскаля сортировка по возрастанию означает, что числа в каждом ряду будут упорядочены так, чтобы число слева было меньше числа справа. Таким образом, ряды Треугольника Паскаля будут отсортированы в порядке возрастания.
| Ряд 0 | Ряд 1 | Ряд 2 | Ряд 3 | ... |
|---|---|---|---|---|
| 1 | 1 | 1 | 1 | ... |
| 1 | 2 | 3 | 4 | ... |
| 1 | 3 | 6 | 10 | ... |
| 1 | 4 | 10 | 20 | ... |
| ... | ... | ... | ... | ... |
Для сортировки массива Паскаля по возрастанию можно применить различные алгоритмы сортировки, такие как сортировка пузырьком, сортировка вставками или сортировка слиянием. При этом, необходимо учитывать особенности структуры Треугольника Паскаля, чтобы правильно обрабатывать числа внутри каждого ряда и между рядами.
Сортировка последовательности чисел треугольника Паскаля в порядке убывания
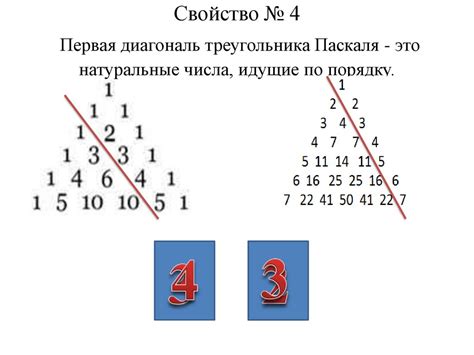
Сортировка последовательности чисел треугольника Паскаля может быть полезна при работе с большим объемом данных, когда требуется определить самые большие числа или выполнить другие операции в порядке убывания их значений. Для этого можно применить различные алгоритмы сортировки, такие как сортировка пузырьком, сортировка вставками или быстрая сортировка.
- Сортировка пузырьком: данная сортировка осуществляет последовательное сравнение и обмен соседних чисел, двигаясь от начала до конца последовательности. Она повторяется до тех пор, пока все числа не будут упорядочены.
- Сортировка вставками: данный алгоритм предполагает проход по последовательности чисел с одновременным вставлением каждого числа на свое место в отсортированной части последовательности.
- Быстрая сортировка: этот алгоритм выбирает опорный элемент в последовательности, а затем разделяет ее на две части: числа, меньшие или равные опорному, и числа, большие опорного элемента. Затем происходит рекурсивное применение сортировки к обеим частям.
Использование этих алгоритмов сортировки позволяет получить последовательность чисел треугольника Паскаля, отсортированную по убыванию. Это может быть полезно при анализе данных и выполнении различных операций в порядке убывания значений.
Определение минимального и максимального значения в упорядоченном ряду чисел Паскаля

В процессе работы с упорядоченным рядом чисел Паскаля возникает необходимость определить минимальное и максимальное значения. Нахождение данных экстремальных значений позволяет лучше понять характеристики и свойства ряда чисел, а также делает возможным проведение дальнейшего анализа и использование этих значений в решении различных задач.
Для определения минимального значения в массиве Паскаля можно использовать подход, основанный на последовательном сравнении каждого элемента с остальными. При проходе по ряду чисел Паскаля сравниваются значения каждой пары соседних чисел и выбирается наименьшее из них. Таким образом, после завершения сравнений, будет найдено минимальное значение в ряде Паскаля.
Аналогично, для определения максимального значения в массиве Паскаля используется подход с последовательным сравнением элементов. В процессе прохода по ряду чисел Паскаля сравниваются значения каждой пары соседних чисел, и выбирается наибольшее из них. По окончанию сравнений будет найдено максимальное значение в упорядоченном массиве Паскаля.
Определение минимального и максимального значений в массиве Паскаля является важным этапом в анализе и использовании ряда чисел. Правильное нахождение экстремальных значений позволяет получить ценную информацию о ряде и использовать ее для достижения поставленных целей и решения задач различной сложности.
Определение среднего значения в структуре треугольника Паскаля

В данном разделе мы рассмотрим способы определения среднего значения в треугольнике Паскаля, абстрактной структуре, имеющей множество применений в математике и программировании. Треугольник Паскаля представляет собой числовой треугольник, в котором каждое число равно сумме двух чисел выше него.
Определение среднего значения в треугольнике Паскаля может быть полезным, например, для вычисления среднего значения ряда чисел или для анализа распределения данных. Мы рассмотрим как итеративный, так и рекурсивный подходы к решению этой задачи, а также приведем примеры кода на различных языках программирования.
Пример кода на языке Python для отображения упорядоченного набора значений Паскаля
Для решения этой задачи мы будем использовать следующий алгоритм:
- Создадим функцию, которая будет генерировать массив Паскаля заданного размера.
- Используя эту функцию, сгенерируем треугольник Паскаля заданного размера и отобразим его на экране.
- Отсортируем значения в полученном массиве Паскаля.
- Выведем отсортированный массив на экране.
Вот пример кода на языке Python, реализующий описанный выше алгоритм:
def generate_pascal_triangle(size):
pascal_triangle = [[1]]
for i in range(1, size):
previous_row = pascal_triangle[i - 1]
current_row = [1]
for j in range(1, i):
current_row.append(previous_row[j - 1] + previous_row[j])
current_row.append(1)
pascal_triangle.append(current_row)
return pascal_triangle
def display_triangle(triangle):
for row in triangle:
print(row)
def sort_pascal_triangle(triangle):
flattened_triangle = [number for row in triangle for number in row]
sorted_triangle = sorted(flattened_triangle)
return sorted_triangle
size = 5
pascal_triangle = generate_pascal_triangle(size)
display_triangle(pascal_triangle)
sorted_triangle = sort_pascal_triangle(pascal_triangle)
print("Sorted Pascal Triangle:", sorted_triangle)
Вопрос-ответ

Как вывести отсортированный массив Паскаля?
Для того чтобы вывести отсортированный массив Паскаля, необходимо сначала сгенерировать его, а затем отсортировать полученный массив чисел. Для генерации массива Паскаля можно использовать треугольник Паскаля - каждое число внутри треугольника равно сумме двух чисел над ним. Затем, полученный массив можно отсортировать с помощью любого алгоритма сортировки, например, пузырьковой сортировки или сортировки вставками. После сортировки можно вывести отсортированный массив Паскаля на экран.
Как извлечь и вывести элементы отсортированного массива Паскаля по возрастанию?
Для извлечения и вывода элементов отсортированного массива Паскаля по возрастанию, необходимо сначала сгенерировать массив Паскаля. Затем, можно отсортировать полученный массив чисел с помощью любого алгоритма сортировки, например, сортировки выбором или быстрой сортировки. После сортировки, можно пройти по отсортированному массиву и вывести его элементы в порядке возрастания на экран или сохранить результат в другой массив.
Как отсортировать и вывести несколько одинаковых значений в отсортированном массиве Паскаля?
Для того чтобы отсортировать и вывести несколько одинаковых значений в отсортированном массиве Паскаля, необходимо сгенерировать массив Паскаля и отсортировать его. Если в массиве Паскаля есть одинаковые значения, то они будут идти подряд. После сортировки можно проходить по отсортированному массиву и выводить на экран значения, проверяя если следующий элемент равен текущему. Таким образом, можно вывести все одинаковые значения на экран или сохранить их в другой массив.



