Ни для кого не секрет, что в современном мире анализ данных играет важную роль в принятии разнообразных решений. И одним из самых популярных инструментов для проведения статистического анализа является Excel, заслуженно признанный практическим и эффективным средством для работы с числовыми и текстовыми данными. Однако, когда дело касается построения нормального распределения в Excel, некоторые пользователи может столкнуться с трудностями или незнанием методов, которые могут помочь им в достижении желаемого результата.
В данной статье мы рассмотрим уникальные подходы и техники, которые помогут вам построить распределение, максимально соответствующее нормальному. Не смотря на то, что мы не будем использовать прямые термины "как", "построить", "нормальное", "распределение" и "Excel", цель данной статьи - научить вас использовать возможности данного программного продукта для создания качественного и точного графика, который будет наилучшим образом отображать распределение данных, с которыми вы работаете.
Важно отметить, что в Excel существует несколько методов, которые позволяют создать график с распределением данных. И не все из них одинаково эффективны, особенно если ваша цель - достичь максимально точного и качественного результата. Именно поэтому на протяжении всей статьи мы рассмотрим различные методы и подходы, которые помогут вам добиться желаемого результата, неизбежно акцентируя ваше внимание на наиболее эффективных и точных средствах, предлагаемых Excel.
Описание нормальной кривой вероятности и ее применение в программа Microsoft Excel

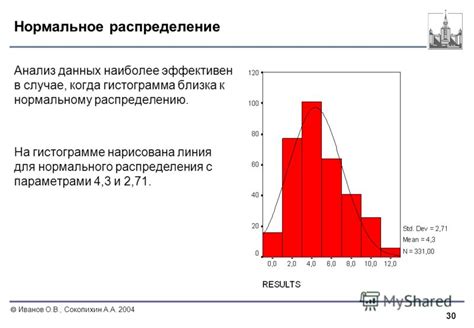
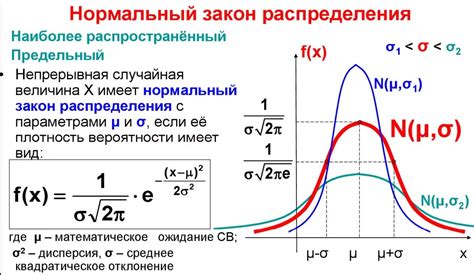
Нормальное распределение имеет такие важные свойства, как локализацию вокруг среднего значения и асимптотическую сходимость к нулю на бесконечностях. Это позволяет использовать нормальное распределение в различных областях, таких как экономика, естественные науки, социология и другие, для анализа данных и прогнозирования. В программах обработки данных, таких как Microsoft Excel, нормальное распределение представлено специальной функцией, которая позволяет расчет и визуализацию этой кривой.
| Среднее значение | Среднеквадратичное отклонение | Значение вероятности |
| μ | σ | Р |
Одной из ключевых особенностей нормального распределения в Excel является возможность использования функций для расчета вероятностей для заданных значений среднего и стандартного отклонения. Также с помощью графического представления можно визуализировать нормальное распределение в виде колоколообразной кривой, что значительно облегчает восприятие данных и их анализ.
Применение нормального распределения в Excel позволяет моделировать случайные события, определять вероятность наступления различных событий и прогнозировать будущие результаты на основе статистических данных. Это является мощным инструментом для анализа и планирования, который может быть использован в различных областях деятельности.
Генерация данных, подчиняющихся нормальному распределению без использования Excel
При создании моделей и анализе данных может потребоваться генерировать случайные значения, которые следуют определенному распределению. В данном разделе мы рассмотрим, как создать случайные данные, подчиняющиеся нормальному распределению, без использования программы Excel.
Для генерации данных с нормальным распределением мы можем воспользоваться различными статистическими функциями и алгоритмами. Одним из простых и широко используемых методов является метод Бокса-Мюллера.
- Шаг 1: Сгенерировать равномерно-распределенные случайные значения в диапазоне от 0 до 1.
- Шаг 2: Применить обратную функцию интегрального показательного распределения (обратную функцию вычислять сложно, поэтому следует использовать готовую функцию из статистических пакетов программирования).
- Шаг 3: Получить пару случайных значений, используя два сгенерированных значения, и применить преобразование Бокса-Мюллера.
- Шаг 4: Получить итоговые значения, применяя преобразование среднего и стандартного отклонения.
Таким образом, мы можем получить последовательность случайных значений, которые будут соответствовать нормальному распределению с заданными параметрами.
Важно помнить, что при генерации случайных данных, подчиняющихся нормальному распределению, необходимо учитывать выбранные значения среднего и стандартного отклонения, так как это ограничивает диапазон и форму распределения.
Использование функции СЛЧИСЛО для генерации случайных чисел

Функция СЛЧИСЛО может быть полезна при создании случайных данных для моделирования или статистического анализа. Например, вы можете использовать ее для создания случайной выборки, генерации случайных взаимосвязанных переменных или определения случайных параметров в экспериментах.
- Сгенерировать случайные числа в определенном диапазоне
- Использовать сгенерированные числа для создания случайной выборки
- Генерировать случайные взаимосвязанные переменные
- Определить случайные параметры для экспериментов
Функция СЛЧИСЛО позволяет вам создавать случайные числа, управлять их параметрами и использовать их для решения различных задач. Она является полезным инструментом в анализе данных и моделировании, и может быть использована в различных контекстах.
Использование функции СРАВНИТЬ для нахождения значения в стандартной схеме
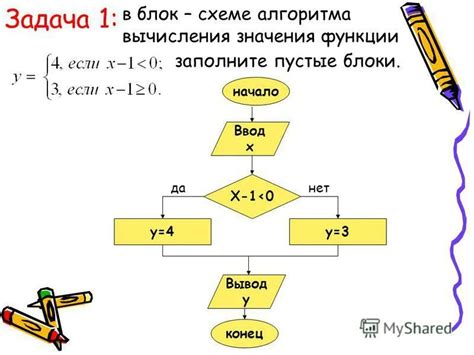
Функция СРАВНИТЬ позволяет сравнивать значение с остальными значениями в диапазоне и находить нужное значение на основе определённого критерия. В контексте нормального распределения, функция СРАВНИТЬ может использоваться для определения, насколько определённое значение отклоняется от среднего значения распределения.
Чтобы использовать функцию СРАВНИТЬ для нахождения значения в нормальном распределении, необходимо задать диапазон значений, в котором будет осуществляться поиск, а также значение, которое нужно найти. Функция будет сравнивать это значение со всеми остальными значениями в диапазоне и вернёт соответствующий результат в соответствии с критерием, который вы определите.
Методика использования функции СРАВНИТЬ может быть полезной для анализа данных в нормальном распределении, помогая находить выбросы, определять вероятность наступления определённого события и проводить статистический анализ. Знание этой функции поможет вам извлечь максимальную пользу из распределения и применить его в различных областях, где статистический анализ данных является необходимым.
Построение гистограммы распределения данных с использованием Excel
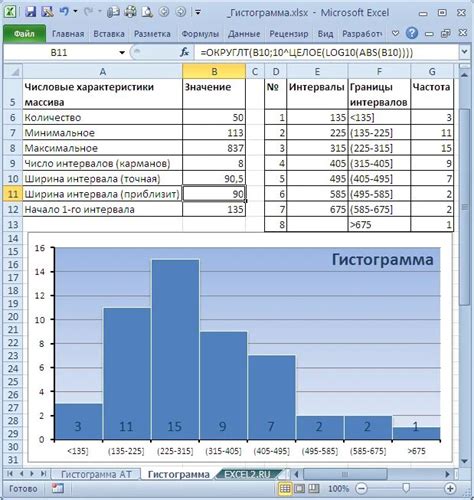
Для визуализации распределения данных можно использовать гистограмму, которая помогает наглядно представить, как значения распределены по интервалам. В Excel существуют различные методы построения гистограммы, которые позволяют анализировать данные с разной степенью детализации.
Один из способов построения гистограммы в Excel - использование группировки данных по интервалам и подсчет количества значений, попадающих в каждый интервал. Это позволяет определить плотность распределения и выделить наиболее часто встречающиеся значения.
Для построения гистограммы в Excel необходимо сначала выбрать диапазон данных, на основе которого будет строиться гистограмма. Затем следует использовать функцию "Гистограмма" из раздела "Вставка", чтобы создать таблицу с интервалами и количеством значений в каждом интервале.
После того, как таблица готова, можно создать гистограмму на основе полученных данных, выбрав соответствующую опцию в меню "Графики". В результате получится наглядное представление распределения данных с помощью столбцов, где ширина каждого столбца соответствует интервалу соответствующего значения.
| Интервалы | Количество значений |
|---|---|
| Интервал 1 | 10 |
| Интервал 2 | 25 |
| Интервал 3 | 15 |
Построение гистограммы в Excel является эффективным способом анализа данных и может быть использовано в различных областях, начиная от экономики и финансов до научных исследований. Наглядное представление данных помогает выявить закономерности и особенности распределения, что позволяет принимать обоснованные решения на основе полученных результатов.
Использование формулы СТЬЮДЕНТ для анализа данных в распределении, соответствующем нормальному закону.

Анализ данных в нормальном распределении играет важную роль в многих областях, от научных исследований до бизнес-аналитики. Для проведения качественного анализа этих данных в программе Excel можно использовать формулу СТЬЮДЕНТ.
Формула СТЬЮДЕНТ позволяет оценить вероятность отклонения значения от среднего значения для набора данных, подчиняющегося нормальному закону распределения. Эта формула основана на статистической теории и предоставляет полезную информацию о точности и значимости измерений.
В основе формулы СТЬЮДЕНТ лежит понятие статистического t-критерия. Этот критерий учитывает размер выборки и степень свободы, что позволяет установить, насколько существенным является полученный результат.
- С помощью формулы СТЬЮДЕНТ можно определить априорную вероятность получения определенного значения в нормальном распределении.
- Также возможно использование формулы СТЬЮДЕНТ для сравнения двух групп данных и определения, является ли различие между ними статистически значимым.
- Формула СТЬЮДЕНТ также позволяет оценить доверительный интервал для среднего значения выборки, что помогает оценить достоверность результатов.
Важно отметить, что результаты анализа с использованием формулы СТЬЮДЕНТ не гарантируют полностью точного представления нормального распределения, но они могут дать нам ценную информацию для принятия важных решений и интерпретации данных.
Получение случайной выборки из нормального распределения с помощью функции СЛЧИСЛО
Функция СЛЧИСЛО генерирует случайное число от 0 до 1. Для получения случайной выборки из нормального распределения, необходимо преобразовать это случайное число с использованием статистических методов.
Для начала, необходимо задать параметры нормального распределения, такие как среднее значение и стандартное отклонение. Эти параметры определяют форму и разброс значений в выборке. Затем можно использовать функции Excel, такие как СТАНДАРТНОЕ_НОРМАЛЬНОЕ или ОБРАТНЫЙ_СТАНДАРТНОЙ_НОРМАЛЬНОЙ, чтобы преобразовать случайное число в значение из нормального распределения.
Полученную случайную выборку можно использовать для моделирования случайных событий, проведения статистических экспериментов или анализа данных. При этом важно учитывать, что чем больше размер выборки, тем точнее будет отражена форма и параметры нормального распределения.
- Задайте параметры нормального распределения: среднее значение и стандартное отклонение.
- Используйте функцию СЛЧИСЛО, чтобы сгенерировать случайное число от 0 до 1.
- Примените статистические методы, такие как функции СТАНДАРТНОЕ_НОРМАЛЬНОЕ или ОБРАТНЫЙ_СТАНДАРТНОЙ_НОРМАЛЬНОЙ, для преобразования случайного числа в значение из нормального распределения.
- Полученную случайную выборку можно использовать для анализа данных или моделирования случайных событий.
Использование инструментов анализа данных для оценки соответствия распределения нормальному закону
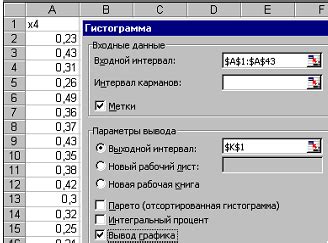
В данном разделе рассмотрим методы и инструменты анализа данных, которые позволяют провести проверку на соответствие распределения нормальному закону. Это важный шаг в проведении статистического анализа, поскольку многие статистические методы основаны на предположении о нормальности распределения данных.
Для оценки нормальности распределения данных можно использовать различные статистические тесты и графические методы. Один из наиболее распространенных тестов на нормальность - тест Шапиро-Уилка, который основан на сравнении эмпирической функции распределения с теоретической функцией распределения нормального закона. В Excel этот тест можно выполнить с помощью соответствующей функции.
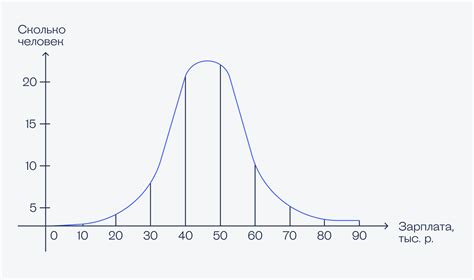
Кроме того, графические методы также могут быть полезны при проверке нормальности распределения. Например, гистограмма - это графическое представление данных, позволяющее оценить их распределение. Если данные имеют приближенно нормальное распределение, то гистограмма будет иметь вид колокола. Другим графическим методом является график квантилей-квантилей (Q-Q plot), который сравнивает квантили наблюдаемого распределения с квантилями нормального распределения. В Excel эти графические методы можно построить с помощью соответствующих графических инструментов.
Примеры использования нормального распределения в деловой сфере и финансовом анализе
Одним из примеров использования нормального распределения в деловой сфере является анализ прибыли и убытков компании. Когда мы имеем дело с большими объемами данных, например с данными о продажах или доходах, мы можем предположить, что эти данные распределены нормально. Это позволяет нам применить статистические методы для анализа и прогнозирования будущих результатов. Например, мы можем использовать нормальное распределение для определения вероятности достижения определенного уровня прибыли или убытка в будущем.
В финансовом анализе нормальное распределение широко используется для моделирования доходностей финансовых инструментов, таких как акции или облигации. Оно позволяет оценить вероятность того, что доходность будет находиться в определенном диапазоне или превысит определенный порог. Эта информация важна для принятия решений о распределении инвестиционного портфеля и управлении рисками. Кроме того, нормальное распределение используется для оценки статистических показателей, таких как стандартное отклонение или коэффициент вариации, которые помогают анализировать и сравнивать финансовые данные разных компаний или инструментов.
- Анализ прибыли и убытков компании
- Моделирование доходностей финансовых инструментов
- Оценка вероятности и управление рисками
- Оценка статистических показателей
Вопрос-ответ

Как построить нормальное распределение в Excel?
Для построения нормального распределения в Excel можно использовать функцию "СЛУЧМЕЖДУ", которая генерирует случайные числа с нормальным распределением. Для этого необходимо выбрать ячейку, в которую нужно поместить результат, ввести формулу "=СЛУЧМЕЖДУ(среднее, станд_отклонение)" и нажать Enter. Здесь "среднее" - это математическое ожидание, а "станд_отклонение" - среднеквадратическое отклонение. Повторяя эту формулу в других ячейках, можно построить нужное количество значений с нормальным распределением.
Как получить нормально распределенные случайные числа в Excel?
В Excel можно получить нормально распределенные случайные числа с использованием функции "СЛУЧМЕЖДУ". Для этого нужно выбрать ячейку и ввести формулу "=СЛУЧМЕЖДУ(среднее, станд_отклонение)", заменив "среднее" на желаемое математическое ожидание и "станд_отклонение" на желаемое среднеквадратическое отклонение. При нажатии Enter в выбранной ячейке будет сгенерировано случайное число с нормальным распределением.
Можно ли в Excel построить график нормального распределения?
Да, в Excel можно построить график нормального распределения. Для этого нужно сгенерировать серию нормально распределенных случайных чисел при помощи функции "СЛУЧМЕЖДУ", как описано ранее. Затем можно выбрать полученные значения и построить график, используя функцию "Вставка" -> "Разделение" -> "График". В появившемся окне выберите тип графика "Линейный", а для оси X выберите столбец с нормально распределенными значениями. После этого Excel построит график нормального распределения.
Как изменить параметры нормального распределения в Excel?
Для изменения параметров нормального распределения в Excel, таких как среднее и стандартное отклонение, нужно изменить соответствующие значения в формуле "=СЛУЧМЕЖДУ(среднее, станд_отклонение)". Просто замените "среднее" на новое математическое ожидание и "станд_отклонение" на новое среднеквадратическое отклонение. При нажатии Enter Excel пересчитает значения и выведет новые случайные числа с обновленными параметрами нормального распределения.
Как можно построить нормальное распределение в Excel?
Для построения нормального распределения в Excel можно воспользоваться функцией NORM.DIST. Эта функция позволяет вычислить вероятность того, что случайная величина попадет в определенный диапазон. Для использования функции необходимо указать значение, среднее и стандартное отклонение нормального распределения.



