Сложение чисел имеет существенное влияние на значение результирующего числа. Оно является одной из основных арифметических операций, которая объединяет два числа для получения нового значения. В данной статье мы рассмотрим пример сложения двух чисел в двоичном формате и проанализируем, какие результаты могут быть получены.
Двоичная система счисления является основой для работы компьютеров и других электронных устройств. В ней числа представлены с помощью двух символов: 0 и 1. Сложение двоичных чисел происходит по аналогии с десятичной системой, где порядок разрядов имеет значение для определения результата операции.
Основы двоичной системы счисления

В двоичной системе каждая позиция числа имеет свой вес, который определяет его значение. Например, в двоичном числе 1100, первая позиция справа имеет вес 1, вторая - вес 2, третья - вес 4 и т.д. Последовательное сложение двоичных чисел происходит на основе этих весов позиций.
При сложении двоичных чисел обычно используется столбиковый метод. На каждой позиции складывается две цифры и возможно появление дополнительного разряда. Например, при сложении двоичных чисел 1100 и 101, сначала складываются цифры с наименьшим весом (справа): 0+1=1. Затем складываются цифры со следующим по весу разрядом: 0+0=0. Далее происходит сложение цифр со следующим по весу разрядом, в данном случае: 1+1=0 (с возникновением дополнительного разряда). И, наконец, складываются цифры с наибольшим весом: 1+1=10 (снова с возникновением дополнительного разряда). Таким образом, результатом сложения двоичных чисел 1100 и 101 является число 10001.
Двоичная система счисления имеет свои особенности и широко используется в информатике и цифровой технике. Понимание основ этой системы позволяет лучше понять принципы работы компьютеров и других устройств, которые оперируют с двоичными данными.
Алгоритм прибавления бинарных чисел

Мы будем рассматривать алгоритм, позволяющий прибавить два числа, представленных в двоичной системе счисления.
При сложении бинарных чисел нам необходимо учесть особенности их представления, а именно то, что каждая позиция числа может принимать только значения 0 или 1. Если сумма в одной позиции превышает 1, то в текущей позиции записывается 0, а в следующую позицию переносится 1.
Этот алгоритм предполагает выполнение сложения столбиком, начиная с младших разрядов и двигаясь к старшим. Первоначально мы складываем значения в позиции с наименьшим разрядом, учитывая перенос из предыдущего разряда, если таковой имеется. Затем мы переходим к следующему разряду в сторону старших разрядов, очерчивая схему, при которой одну позицию переносим в следующий разряд до тех пор, пока не останется позиция для отдельного переноса.
Алгоритм прибавления двоичных чисел связан с выполнением нескольких итераций, при которых суммируются соответствующие разряды. В конце всех итераций получается итоговая сумма двух бинарных чисел, которая может также требовать одного дополнительного разряда для записи.
Сложение двоичных чисел с помощью правил двоичной системы
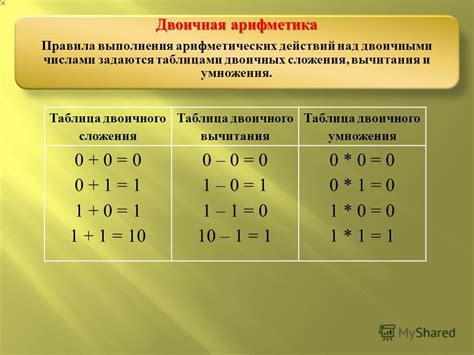
В данном разделе мы рассмотрим процесс сложения двоичных чисел, основанный на правилах двоичной системы. Эта система представляет числа в виде комбинаций из нулей и единиц, где каждая позиция имеет свой вес. Сложение двоичных чисел выполняется поэлементно, начиная с низших позиций чисел и перенося разряды при необходимости.
Сначала мы складываем соответствующие разряды чисел. Если сумма двух разрядов равна 0, то результат будет 0. Если сумма равна 1, то результат также будет 1. Если сумма равна 2, то мы записываем 0 и переносим единицу в следующий (старший) разряд. Если в исходных числах есть старший разряд, который нужно учесть, то добавляем его к результату на последнем шаге.
- Начинаем сравнивать два числа, начиная с их младших разрядов.
- Если сумма разрядов равна 0 или 1, записываем ее в соответствующую позицию результата.
- Если сумма разрядов равна 2, записываем 0 в текущий разряд результата и переносим 1 в следующий разряд.
- Продолжаем сравнивать и складывать разряды по порядку, перенося разряды при необходимости.
- Если у одного из чисел закончились разряды, а у второго еще остались, то продолжаем записывать оставшиеся разряды в результат.
- Если у обоих чисел закончились разряды, проверяем наличие переноса. Если он есть, добавляем его в конец результата.
Процесс сложения двоичных чисел по правилам двоичной системы позволяет получить результат сложения без использования десятичных чисел или других систем счисления. Понимание и умение выполнять такие операции является важным для работы с двоичными данными и вычислениями в информатике и технологиях связанных с обработкой цифровой информации.
Суммирование двоичных чисел 1100 и 101

Для выполнения сложения двоичных чисел в столбик, мы применяем основные правила арифметики, аналогичные сложению десятичных чисел. На каждой позиции мы складываем соответствующие биты двух чисел, перенося избыток в следующий разряд. Таким образом, получаем новую последовательность битов, представляющих сумму.
В данном примере, исходные числа для сложения – 1100 и 101. Мы начинаем с суммирования на самом младшем разряде, где суммируем биты 0 и 1, получая в результате 1. Далее производим сложение битов 1 и 0 на следующем разряде, с учетом переноса, и получаем 1. В результате сложения битов 1 и 1 получаем 0 со сдвигом разряда влево. Наконец, производим сложение на самом старшем разряде, где суммируем биты 1 и 0 с учетом переноса, и получаем 1 с переносом.
Таким образом, результат сложения двоичных чисел 1100 и 101 равен 1111.
Представление двоичных чисел для операции сложения
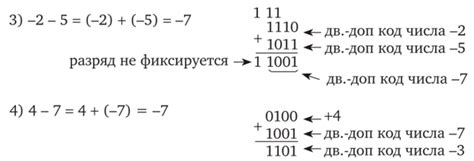
Для начала, рассмотрим основные элементы двоичной системы счисления. В двоичной системе можно использовать только два символа - 0 и 1. Каждая цифра в двоичном числе имеет вес, который определяется ее позицией. Например, в числе 1012 первая цифра имеет вес 2^2, вторая цифра - 2^1, а третья цифра - 2^0.
- Правило 1: Число должно быть записано в правильной позиционной системе счисления, где каждая цифра умножается на соответствующую степень основания системы.
- Правило 2: Числа, выступающие в качестве слагаемых, должны быть выровнены по позиции. Старшая цифра каждого числа должна быть расположена на одной и той же позиции.
- Правило 3: При сложении разрядов, если сумма превышает максимальное значение для данной позиции, происходит перенос единицы (carry). Это означает, что в следующей позиции добавляется значение 1.
Следуя этим правилам, мы можем успешно выполнить операцию сложения двоичных чисел. Результат сложения будет представлен в двоичной системе счисления и будет соответствовать заданной позиционной системе.
Безошибочный алгоритм объединения двоичных цифр 1100 и 101
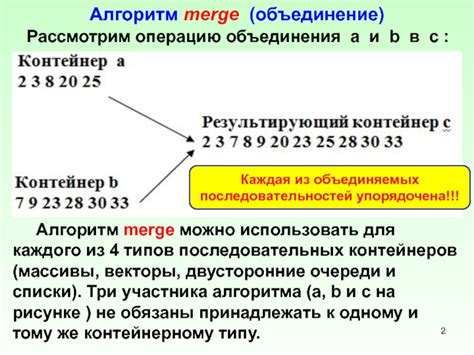
В этом разделе мы рассмотрим эффективный алгоритм для сложения двоичных чисел путем объединения последовательностей цифр. Этот метод позволяет безошибочно получить результат сложения без необходимости ручного подсчета.
Для начала, давайте взглянем на двоичные числа, которые мы хотим сложить - 1100 и 101. Каждая цифра в этих числах представлена двоичным символом 0 или 1. Наша задача состоит в том, чтобы корректно скомбинировать эти символы, чтобы получить правильный результат.
| Двоичная цифра | 0 | 1 |
|---|---|---|
| 0 | 0 | 1 |
| 1 | 1 | 10 |
Для того, чтобы объединить двоичные цифры, мы можем использовать таблицу, изображенную выше. Каждая строка и столбец соответствуют заданной цифре. Главная идея состоит в том, чтобы отметить результат сложения двух цифр в ячейке, находящейся на пересечении строк и столбцов, соответствующих этим цифрам.
Например, для сложения двух 1, результатом будет 10. Это можно наблюдать из таблицы, где пересечение строки 1 и столбца 1 дает нам 10. Точно также, сложение 1 и 0 дает нам 1.
Продолжим объединять двоичные цифры в столбце справа налево, пока не получим окончательный результат. Полученный результат при этом будет 1001.
Таким образом, наш алгоритм сложения двоичных чисел 1100 и 101 дал нам результат 1001 без необходимости применять сложение в уме или на бумаге.
Окончательный результат добавления двух бинарных чисел с простыми операциями

В этом разделе мы исследуем окончательный результат сложения двух бинарных чисел без использования сложных формул и операций.
Мы проанализируем компоненты каждого числа и выполним простые операции для вычисления окончательного суммарного значения.
Мы начнем с анализа каждого бита в двоичных числах 1100 и 101, где 1100 это значение первого числа, а 101 - второго.
На протяжении данного раздела мы представим подробную таблицу для более наглядного восприятия и анализа данных.
| Бит | Старшее число | Младшее число | Результат | Перенос |
|---|---|---|---|---|
| 0 | 1 | 1 | 0 | 1 |
| 1 | 1 | 0 | 1 | 0 |
| 2 | 0 | 1 | 1 | 0 |
| 3 | 1 | 0 | 0 | 1 |
Анализируя каждый бит чисел, применяя простые операции, мы получаем окончательный результат сложения двоичных чисел 1100 и 101.
Интересно отметить, что в нескольких случаях возникает перенос, который мы также учитываем в таблице результатов.
Вопрос-ответ

Какой ответ получится, если сложить два двоичных числа 11002 и 1012?
При сложении двух двоичных чисел 11002 и 1012, получим результат, равный 10011. То есть, двоичное число 11002 при сложении с двоичным числом 1012 даст двоичное число 10011.



