В школьной программе математики, на уроках арифметики, мы изучаем различные методы решения задач. Одним из важных понятий, которое нам пригодится в будущем, является наибольший общий делитель (НОД). В этой статье мы рассмотрим один из способов нахождения НОД трех чисел.
НОД - это наибольшее число, которое одновременно является делителем всех заданных чисел. Всегда полезно знать эту величину, особенно при решении задач, связанных с дробями, пропорциями и многими другими арифметическими операциями. Ведь знание наибольшего общего делителя помогает нам сокращать дроби и находить простейшие числовые значения.
Однако, в первую очередь, нам необходимо разобраться с терминологией. Давайте вспомним, что такое делители числа. В то время как НОД является общим для всех чисел, делители - это числа, на которые исходное число делится без остатка. Например, если мы рассматриваем число 12, его делители будут 1, 2, 3, 4, 6 и само число 12. Разобравшись с этими основными понятиями, мы готовы перейти к решению задачи нахождения НОД трех чисел.
Определение НОД (Наибольший Общий Делитель)

Наибольший Общий Делитель, или НОД, можно представить как самое большое число, которое одновременно является делителем для всех заданных чисел. НОД позволяет нам определить, существует ли общий делитель для данных чисел, а также найти его наибольшее значение. Это полезное понятие используется во многих областях математики и находит применение при решении различных задач.
Например:
Для двух чисел, таких как 12 и 18, НОД будет равен 6, так как 6 является наибольшим общим делителем для обоих чисел. То есть, 6 делит оба числа без остатка, а никакое большее число уже не подойдет.
В следующих разделах мы рассмотрим различные методы нахождения НОД для двух и более чисел, а также примеры задач, в которых данное понятие применяется.
Метод деления с остатком: эффективный способ нахождения НОД в мировом языке чисел
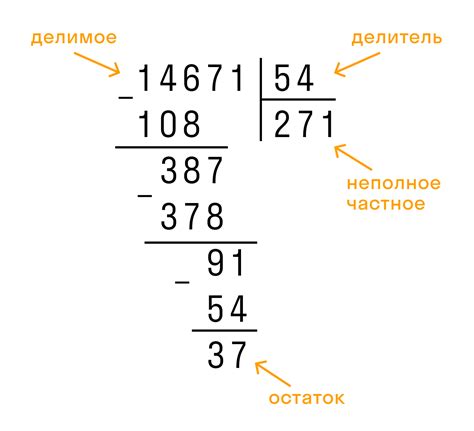
Прежде чем мы погрузимся в применение метода, давайте разберемся, что такое деление с остатком. Это процесс, при котором мы делим одно число на другое и получаем как результат целую часть от деления и остаток. Остаток, по сути, представляет собой то, что остается после вычитания целого числа от исходного числа.
Метод деления с остатком для нахождения НОД основан на простой идеи: если у нас есть три числа, то НОД этих трех чисел будет также являться НОДом НОДа двух из них и оставшегося числа. Мы продолжаем применять эту идею, пока не найдем наибольший общий делитель для всех трех чисел.
Теперь, когда у нас есть общее представление о методе деления с остатком и его применении для нахождения НОД, давайте перейдем к конкретному примеру, чтобы увидеть его в действии.
- Шаг 1: Выберите любые три числа, для которых вы хотите найти НОД.
- Шаг 2: Разделите первое число на второе число и запишите результат в виде целой части и остатка.
- Шаг 3: Делите второе число на остаток, который получен на предыдущем шаге, и снова запишите результат в виде целой части и остатка.
- Шаг 4: Продолжайте делить последнее остаток на текущий остаток до тех пор, пока остаток не станет равным нулю.
- Шаг 5: Последнее ненулевое число в остатках будет являться НОДом выбранных трех чисел.
Используя этот метод, вы сможете быстро и эффективно находить НОД для трех чисел, не только в математике, но и в реальной жизни, где знание методов решения проблем является незаменимым навыком.
Примеры алгоритмов для нахождения наибольшего общего делителя трех чисел

В данном разделе представлены несколько примеров алгоритмов, при помощи которых можно определить наибольший общий делитель трех чисел. Такие алгоритмы помогут вам легко и быстро находить НОД для любой тройки чисел.
Первым примером является алгоритм поиска НОД трех чисел с помощью пошагового деления. При использовании этого метода, осуществляется последовательное деление на каждое из входящих чисел. Процесс продолжается до тех пор, пока не будет достигнуто наибольшее число, на которое все три числа делятся без остатка. Таким образом, получается наибольший общий делитель.
Вторым примером является алгоритм поиска НОД трех чисел с помощью метода Эвклида. При использовании этого метода, из трех чисел на каждом шаге выбираются два, для которых находится НОД с помощью алгоритма Евклида для двух чисел. Затем, найденный НОД сравнивается с третьим числом и процесс повторяется до тех пор, пока не будет достигнуто наибольшее число, на которое все три числа делятся без остатка.
Третьим примером является алгоритм поиска НОД трех чисел с помощью факторизации. При использовании этого метода, каждое из чисел представляется в виде произведения простых множителей. Затем, находим наименьший по степени простой множитель, который встречается в каждом из чисел. Этот множитель и будет наибольшим общим делителем для трех чисел.
Правило делимости и его применение для определения наибольшего общего делителя

В данном разделе мы рассмотрим основное правило делимости, которое позволяет нам определить наибольший общий делитель двух или более чисел. Используя эту важную математическую концепцию, мы сможем эффективно находить общие делители и их наибольшее значение.
Роль простых чисел в определении наибольшего общего делителя (НОД)

Простые числа, как ключевой фактор в поиске НОД, помогают нам разложить каждое из трех чисел на простые множители. Далее, применяя свойства НОД, мы выделяем общие простые множители и находим их наименьшую степень. Сочетая эти простые множители снова, мы получаем НОД трех чисел.
Представив числа через простые множители и найдя их общие, мы получим информацию о наибольшем общем делителе этих чисел. НОД помогает нам определить, какие числа делятся нацело на все три исходных числа без остатка.
Понимание роли простых чисел в процессе нахождения НОД позволяет нам эффективно работать с большими числами, разбивая их на более простые составляющие, и тем самым выполнять сложные задачи наиболее точно и быстро.
Практическая польза от использования ГСД трех чисел

Нахождение ГСД трех чисел может быть использовано при определении наименьшего общего кратного (НОК), которое является необходимым во многих сферах жизни. Например, при планировании маршрута путешествия на автомобиле, необходимо знать, через какие промежуточные города следует проехать, чтобы минимизировать пройденное расстояние. Здесь нахождение ГСД трех чисел позволяет определить оптимальное число промежуточных городов и сэкономить время и топливо.
Также, нахождение ГСД трех чисел может быть полезно при решении задач в сфере электроники. Например, при проектировании электрической схемы, необходимо выбрать резисторы с определенным номиналом, чтобы достичь требуемого значения сопротивления. Здесь ГСД трех чисел помогает определить общий множитель, который будет использоваться для выбора оптимальных резисторов.
Кроме того, нахождение ГСД трех чисел применимо в области финансов. Например, при расчете эффективного ставления по вложениям или кредитам, ГСД трех чисел может помочь определить наименьший общий делитель суммы и срока, что позволит получить более точные результаты и принять обоснованные финансовые решения.
Таким образом, нахождение ГСД трех чисел имеет практическую ценность и может быть широко применено в различных областях. Знание и использование этой концепции помогает решать задачи более эффективно и принимать обоснованные решения на основе математических принципов.
Вопрос-ответ

Каким способом можно найти НОД трех чисел?
НОД трех чисел можно найти с помощью метода последовательного деления.
Можно ли использовать алгоритм Эвклида для нахождения НОД трех чисел?
Нет, алгоритм Эвклида применяется для нахождения НОД двух чисел, поэтому для трех чисел нужно использовать другой метод.
Какой алгоритм следует использовать для нахождения НОД трех чисел в 5 классе?
В 5 классе можно использовать метод последовательного деления, который заключается в поиске общих делителей всех трех чисел.
Существуют ли какие-то правила для выбора трех чисел при нахождении их НОД в 5 классе?
При выборе трех чисел для нахождения их НОД необходимо выбирать числа таким образом, чтобы они были достаточно большими и имели общие делители.
Есть ли какие-то дополнительные приемы или советы для упрощения процесса нахождения НОД трех чисел в 5 классе?
Да, можно использовать факторизацию чисел, то есть разложение каждого числа на простые множители, чтобы упростить поиск их общих делителей.
Как найти НОД трех чисел в 5 классе математики?
Для нахождения НОД (наибольшего общего делителя) трех чисел в 5 классе математики можно воспользоваться методом последовательного деления или методом факторизации чисел.
Каким способом проще найти НОД трех чисел: методом последовательного деления или методом факторизации?
Оба способа подходят для нахождения НОД трех чисел, и выбор способа зависит от предпочтений и уровня понимания ребенка. Метод последовательного деления может быть проще в понимании, но метод факторизации является более эффективным и быстрым.



