Все великие открытия исходят из простых и базовых представлений. Рассмотрим, к примеру, треугольники. Это одни из самых простых и изучаемых геометрических фигур. Однако, они скрывают в себе неисчерпаемый потенциал для расчетов и анализа различных параметров, включая площади. Понимание отношения площадей треугольников является не только ключом к их изучению, но и обеспечивает основу для более сложных геометрических исследований.
Важно отметить, что понятие площади треугольника может быть применено во множестве практических задач и процессов. От строительства зданий и дизайна интерьера до разработки дорожных маршрутов и оптимизации производственных процессов, точные расчеты площадей треугольников играют решающую роль в определении эффективности и точности работ. Поэтому, освоение методов расчета отношений площадей треугольников не только академически значимо, но и имеет прямое приложение в реальном мире.
Исследование отношения площадей треугольников является одним из ключевых аспектов математического анализа. Оно позволяет нам погрузиться в принципы геометрии, рассмотреть различные способы измерения и анализа площадей и исследовать зависимости между этими параметрами. Методы расчета отношения площадей треугольников достаточно разнообразны и вариативны, и понимание их сути дает базу для более глубокого изучения геометрических и даже физических процессов.
Расчет площади треугольника: основные методы

В данном разделе мы рассмотрим различные способы определения площади треугольника. Изучение этих методов поможет нам более глубоко понять, как можно вычислить площадь данной геометрической фигуры, используя разные подходы.
Один из самых простых методов для расчета площади треугольника основан на измерении длин его сторон. Мы можем использовать известные формулы и теоремы, такие как теорема Пифагора или закон синусов, чтобы определить значения сторон треугольника и затем применить формулу для вычисления площади.
Еще одним способом расчета площади треугольника является использование высоты, проведенной из одной из его вершин. Высота разделяет треугольник на две прямоугольные половины, и площадь каждой половины может быть вычислена с использованием формулы для площади прямоугольника.
Кроме того, мы можем использовать формулу Герона, которая основана на длинах всех трех сторон треугольника. Этот метод является более сложным, но более общим, так как он подходит для треугольников любой формы.
| Метод | Принцип | Преимущества |
|---|---|---|
| Измерение сторон | Использование формул и теорем для определения сторон треугольника и последующий расчет площади | Простота использования при известных значениях сторон |
| Использование высоты | Измерение высоты и использование формулы для площади прямоугольника | Позволяет расчитать площадь, зная только одну сторону и высоту |
| Формула Герона | Использование длин всех сторон для определения площади | Применима для треугольников любой формы |
Геометрическое понятие площади треугольника

Площадь треугольника определяется путем измерения его поверхности, то есть области, которую занимают вершины треугольника и все точки, лежащие внутри него. В геометрии существует несколько способов вычисления площади треугольника, которые мы подробно рассмотрим в последующих разделах.
- Один из подходов к расчету площади треугольника - использование длин его сторон и геометрических формул.
- Второй метод основан на использовании высоты треугольника и одной из его сторон.
- Третий способ - разбиение треугольника на более простые геометрические фигуры, для которых уже известны формулы для расчета площади.
Выбор метода расчета площади треугольника зависит от доступных данных о его сторонах и углах, а также от конкретных условий задачи, в которой требуется определить площадь. Выбирая оптимальный метод, мы сможем эффективно и точно вычислить площадь треугольника и использовать это значение в дальнейших вычислениях или решении геометрических задач.
Метод Герона: эффективный подход к вычислению площади треугольника

Раздел "Метод Герона для расчета площади треугольника" представляет эффективную технику, которая позволяет определить площадь треугольника, используя лишь длины его сторон и математические операции. Этот метод основан на формуле Герона, которая была разработана древнегреческим математиком Героном Александрийским.
Во многих практических ситуациях может возникнуть необходимость быстро определить площадь треугольника без доступа к его высоте или углам. Метод Герона позволяет решить эту задачу, используя только известные длины сторон треугольника.
Преимущество метода Герона заключается в его простоте и эффективности. Он подходит для нахождения площади треугольника любой формы и включает в себя всего несколько математических операций. Это делает его особенно полезным в программировании и других областях, где требуется быстрый и надежный расчет площади треугольника.
Чтобы применить метод Герона, необходимо знать длины всех трех сторон треугольника. По этим данным можно вычислить полупериметр треугольника, а затем использовать его в формуле Герона для расчета площади. Окончательный результат представляет собой числовое значение, которое показывает площадь треугольника, выраженную в квадратных единицах площади.
Метод Герона является универсальным и надежным способом вычисления площади треугольника. Он может быть легко реализован в различных языках программирования, а также применен в различных областях, где требуется нахождение площади треугольника на основе известных данных о его сторонах.
Важно отметить, что метод Герона применим только для треугольников, длины всех сторон которых могут образовать треугольник, иначе результатом будет некорректное значение площади.
Способ Герона и его преимущества

Основная идея метода Герона заключается в разбиении треугольника на несколько более простых фигур, таких как прямоугольники и треугольники. Затем мы находим площади этих фигур и суммируем их, чтобы получить площадь исходного треугольника. Таким образом, мы обращаем сложную задачу в более простые шаги, что облегчает расчеты.
Преимуществами метода Герона являются его простота и универсальность. Он может быть применен для решения задач с треугольниками любой формы и размера. Независимо от того, является ли треугольник прямоугольным, равнобедренным или произвольным, способ Герона дает нам возможность быстро и точно рассчитать его площадь.
Кроме того, этот метод позволяет использовать общие формулы и алгоритмы для вычислений, что делает его удобным в практическом применении. Мы можем легко расчеть площадь треугольника, используя простые математические операции, такие как вычисление корня или возведение в квадрат, что делает способ Герона доступным и понятным для широкого круга людей.
Способ Герона и его ограничения

Проблема точности. Метод Герона основан на формуле, которая предполагает прямолинейность сторон треугольника и отсутствие погрешностей в измерениях. Однако в реальности это далеко не всегда выполняется. Небольшие изменения в измерениях или несовершенство фигуры могут существенно искажать результаты расчетов.
Ограничения формы треугольников. Метод Герона предназначен для расчета площадей обычных треугольников, у которых все стороны известны. Однако, при наличии особых форм треугольника, например, когда одна из сторон равна нулю, метод может давать некорректные результаты. В таких случаях необходимо использовать другие методы расчета.
Отсутствие учета высоты треугольника. Метод Герона, основываясь на формуле полупериметра, не учитывает высоту треугольника. В результате этого метода нельзя определить площадь треугольника, если известны лишь его стороны, но неизвестна его высота. В таких случаях стоит использовать другие методы расчета.
Метод полупериметра: эффективный способ для определения площади треугольника

В отличие от других методов, где необходимо знать длины сторон или углы треугольника, метод полупериметра позволяет вычислить площадь треугольника, используя только значения его сторон. Этот метод особенно полезен, когда точные значения углов или длин сторон сложно определить или недоступны.
Для использования метода полупериметра необходимо знать длины всех трех сторон треугольника. По этим значениям можно вычислить полупериметр, а затем с использованием формулы Герона определить площадь треугольника. Кроме того, метод полупериметра может быть расширен для треугольников, у которых известны только длины двух сторон и угол между ними.
Метод полупериметра является удобным инструментом для расчета площади треугольника в различных ситуациях. Он позволяет эффективно решать задачи, связанные с расчетами площадей треугольников, особенно при ограниченном наборе данных. Использование этого метода упрощает процесс расчета и позволяет получить точный результат без лишних усилий.
Расчет площади треугольника через высоту
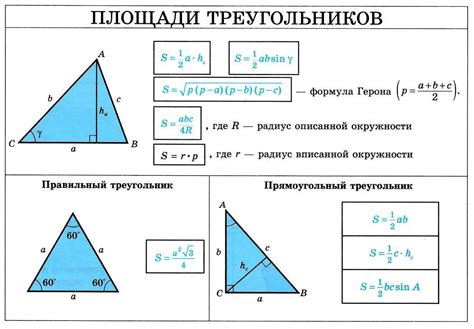
Для расчета площади треугольника через высоту необходимо знать значение высоты и длины основания треугольника. Площадь треугольника равна произведению половины длины основания на длину высоты. В дальнейших расчетах можно использовать таблицу для наглядности и удобства.
| Параметр | Обозначение | Значение |
|---|---|---|
| Длина основания | b | ... |
| Высота треугольника | h | ... |
| Площадь треугольника | S | ... |
Используя значения длины основания (b) и высоты треугольника (h), можно просто и быстро вычислить площадь треугольника (S) по формуле:
S = (b * h) / 2
Расчет площади треугольника через высоту предоставляет возможность получить точные значения площади треугольника без необходимости знания длин всех его сторон. Этот метод особенно полезен, когда вам известны только длина основания и высота треугольника.
Вопрос-ответ

Какие методы можно использовать для расчета отношения площадей треугольников?
Существует несколько методов для расчета отношения площадей треугольников, включая метод геометрического построения, метод полупериметров и метод синусов.
Как работает метод геометрического построения для расчета отношения площадей треугольников?
Метод геометрического построения основан на использовании подобия треугольников. Для расчета отношения площадей необходимо построить два треугольника, один вложенный в другой, таким образом, чтобы они были подобны. Затем можно вычислить отношение длин сторон или отношение площадей треугольников.
Как работает метод полупериметров для расчета отношения площадей треугольников?
Метод полупериметров основан на использовании формулы Герона для нахождения площади треугольника. Сначала необходимо вычислить полупериметры обоих треугольников, затем подставить полученные значения в формулу Герона и вычислить площади треугольников. Отношение площадей будет равно отношению площадей.
Как работает метод синусов для расчета отношения площадей треугольников?
Метод синусов использует тригонометрическое соотношение для вычисления площади треугольника. Необходимо найти синусы углов треугольников и подставить их в формулу площади. Затем можно вычислить отношение площадей треугольников, используя полученные значения.



