Термины, уравнения, расчеты - все это может показаться сложным и запутанным. Однако, когда дело касается нахождения площади прямоугольника, все на самом деле довольно просто. Забудьте о сложных формулах и запоминании разных правил - мы покажем вам способы, которые даже школьник сможет понять.
Величина площади прямоугольника может быть важным параметром при проектировании, строительстве и даже при решении повседневных задач. Регулярная фигура с параллельными сторонами и прямыми углами, привлачивает своей простотой и рациональностью. Поэтому иметь возможность вычислить площадь прямоугольника - очень полезное умение.
Вам необходимо знать лишь значимые параметры - длины двух смежных сторон, и вы сможете легко вычислить площадь. Не нужно быть экспертом в математике, достаточно знать пару трюков и уметь воспользоваться простыми формулами. Мы расскажем вам о самых популярных методах - таких, которые помогут вам в повседневной жизни и при решении профессиональных задач. Приготовьтесь удивить своих друзей и коллег умением мгновенно вычислять площадь прямоугольника!
Раздел: Основы измерения площади прямоугольника
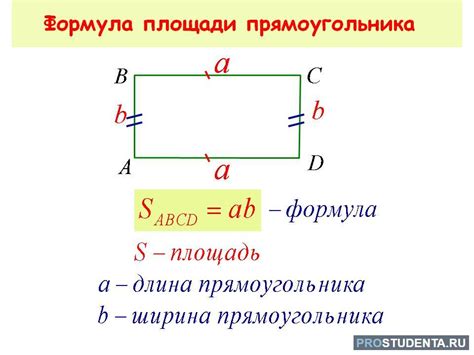
Понимание и определение площади является важным элементом для измерения протяженной фигуры, такой как прямоугольник. Площадь прямоугольника - это общая поверхность, занимаемая этим двухмерным объектов, и она всегда выражается в квадратных единицах.
Для вычисления площади прямоугольника существует основная формула, основанная на измерениях его сторон. Первый шаг - найти длину одной из сторон прямоугольника, а затем умножить ее на длину соседней стороны. Это позволяет получить площадь в квадратных единицах (например, квадратных метрах или квадратных дюймах) и измерить протяженность желаемой поверхности.
Важно помнить, что стороны прямоугольника могут быть представлены разными переменными, такими как a и b, или их кратными множителями. Поэтому при расчете площади необходимо убедиться, что соответствующие длины сторон правильно отождествлены и правильно умножены друг на друга.
Изучаем формулу и правила

В этом разделе мы погрузимся в глубины формулы, которая поможет нам расчитать площадь прямоугольника. Мы узнаем о правилах её применения и разберемся, как применить эти знания на практике.
Формула, которую мы рассмотрим, является ключевым инструментом при расчете площади прямоугольника. Она позволяет определить размеры фигуры, используя разные параметры и операции.
Важно знать основные шаги для вычисления площади прямоугольника и следовать им без исключений. Также необходимо учитывать, что формула может варьироваться в зависимости от используемых величин и их взаимоотношений.
Погрузимся в хитрости и секреты формулы, чтобы стать более компетентными в решении задач на площадь прямоугольника!
Примитивный способ: измеряем стороны и умножаем
В этом разделе мы рассмотрим простой и доступный способ расчета площади прямоугольника, который не требует использования формул и сложных математических выкладок. Для этого достаточно измерить длину и ширину прямоугольника и умножить эти значения друг на друга.
Измерение сторон
Перед началом расчета площади прямоугольника необходимо точно измерить его стороны. Для этого можно использовать линейку, рулетку или другие инструменты для измерения длины. Не забывайте, что длина и ширина прямоугольника должны быть измерены в одной и той же единице измерения.
Умножение сторон
После того, как вы получили значения длины и ширины прямоугольника, умножьте их друг на друга. Результат этого умножения будет являться площадью прямоугольника. Не забудьте указать единицу измерения площади, чтобы окончательный ответ был полностью понятен.
Примечание: этот способ расчета дает точный результат только в случае, если прямоугольник имеет прямые углы и все его стороны измеряются с высокой точностью.
Нахождение площади прямоугольника по диагонали

В этом разделе мы рассмотрим один из методов расчета площади прямоугольника, который основан на известной диагонали прямоугольника. Этот метод позволяет найти площадь без знания длин сторон и углов прямоугольника, что может быть полезно в некоторых ситуациях.
Для вычисления площади прямоугольника по диагонали нам понадобится знание только длины диагонали и формула для расчета. Ниже приведена формула для нахождения площади, основанная на длине диагонали:
- Разложите прямоугольник на два равнобедренных треугольника, с углами при вершине диагонали.
- Найдите длину одной из сторон треугольника с помощью теоремы Пифагора.
- Умножьте длину этой стороны на длину диагонали и поделите полученное значение пополам, чтобы найти площадь одного треугольника.
- Умножьте площадь треугольника на 2, чтобы получить общую площадь прямоугольника.
Используя этот метод, вы сможете вычислить площадь прямоугольника, имея только длину его диагонали. Это особенно полезно, когда вам неизвестны другие геометрические параметры прямоугольника.
Разнообразные расчеты площади прямоугольника

В данном разделе представлены уникальные примеры, демонстрирующие различные методы расчета площади прямоугольника. Мы рассмотрим разные подходы к определению этого значения, используя разнообразные формулы и приемы.
Пример 1: Предположим, у нас есть прямоугольник, длина его стороны обозначается буквой "а", а ширина - буквой "в". В данном случае, площадь прямоугольника можно найти, умножив значение длины на ширину: площадь = а * в. Найдем, например, площадь прямоугольника со сторонами "5" и "8": площадь = 5 * 8 = 40.
Пример 2: Другой способ расчета площади прямоугольника - использование диагонали. Если известна длина диагонали "d" и угол "α" между диагональю и одной из сторон прямоугольника, можем воспользоваться следующей формулой: площадь = (d² * sin(α)) / 2. Рассмотрим пример: площадь прямоугольника, у которого диагональ равна "10" и угол между диагональю и одной из сторон равен "30°". Вычисляем: площадь = (10² * sin(30°)) / 2 = (100 * 0.5) / 2 = 50 / 2 = 25.
Пример 3: Допустим, у нас имеются только данные о периметре прямоугольника и круглим значение до двух знаков после запятой. В таком случае, мы можем использовать следующую формулу для расчета площади: площадь = (периметр² - 16) / 4. Предположим, периметр прямоугольника равен "18". Тогда, площадь можно рассчитать следующим образом: площадь = (18² - 16) / 4 = (324 - 16) / 4 = 308 / 4 = 77.
Таким образом, познакомившись с различными методами расчета площади прямоугольника, вы можете выбрать подходящий способ в зависимости от информации, которая вам известна. Используйте рассмотренные примеры как руководство при решении задач и расчета площади данной фигуры.
Раздел: Рассчитываем площадь четырехугольника со сторонами 5 и 8
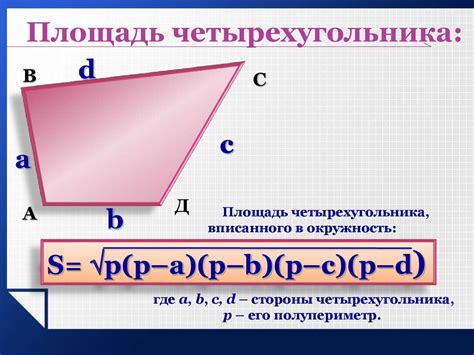
Для этого воспользуемся формулой, соответствующей прямоугольнику: площадь равна произведению длин его сторон. В данном случае, у нас имеется прямоугольник с длиной одной стороны 5 и длиной другой стороны 8. Применяя формулу, получим площадь такой фигуры.
Рассчитаем площадь прямоугольника: площадь = длина первой стороны * длина второй стороны. В данном случае, площадь = 5 * 8 = 40. Таким образом, площадь прямоугольника со сторонами 5 и 8 равна 40 единицам площади.
Это всего лишь один из примеров расчета площади прямоугольника, и теперь вы знаете, как просто найти площадь данной фигуры, имея значения длин ее сторон. Вам достаточно применить соответствующую формулу и выполнить несложные арифметические вычисления.
Площадь прямоугольника с известной стороной и диагональю
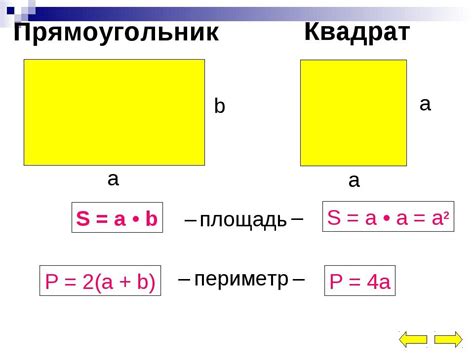
В данном разделе рассмотрим случай, когда известна только одна сторона прямоугольника и его диагональ. Уравнение для расчета площади прямоугольника в таком случае может быть полезным при необходимости определить площадь фигуры без информации о другой стороне.
Для расчета площади прямоугольника, когда известна одна сторона и диагональ, необходимо воспользоваться свойствами прямоугольника. Зная, что диагональ прямоугольника является гипотенузой прямоугольного треугольника, можно воспользоваться теоремой Пифагора для нахождения второй стороны.
Предположим, что сторона прямоугольника, известная нам, равна a, а диагональ прямоугольника равна d. По теореме Пифагора получаем следующее уравнение: a^2 + b^2 = d^2, где b - вторая сторона прямоугольника.
Решим уравнение относительно b, применив соответствующие математические операции. Полученное значение b можно использовать для расчета площади прямоугольника с известной стороной и диагональю по формуле S = a * b.
Таким образом, зная одну сторону и диагональ прямоугольника, вы можете вычислить площадь фигуры без необходимости знать значение второй стороны.
Вопрос-ответ

Какая формула используется для расчета площади прямоугольника?
Для расчета площади прямоугольника используется формула: Площадь = Длина * Ширина.
Как найти площадь прямоугольника, если известны его длина и ширина?
Если известны длина (а) и ширина (b) прямоугольника, то площадь (S) можно найти умножив длину на ширину: S = a * b.
Можно ли найти площадь прямоугольника, если известна только периметр?
Нет, найти площадь прямоугольника нельзя, если известен только периметр. Для расчета площади необходимо знать либо длину и ширину, либо другие параметры, такие как углы или диагонали.



