Круговорот существует во вселенной, а числа отражают его гармонию и бесконечность. Среди множества различных чисел, ряд особенных цифр дарят нам удивительные пазлы для разгадки. Сегодня мы исследуем этот маленький уголок школьного математического мира, который так глубоко возносит нас в неведомое, а именно - таинственные и загадочные числа, которые неподвластны любым делителям.
Когда мы говорим о числах, складываются впечатления и ассоциации у каждого из нас. Это капитаны наших финансов, творцы наших математических головоломок, ключи к шифрам и алгоритмам. В 6 классе, в самом начале школьного пути, мы встречаемся с множеством странных цифр, некоторые из которых скрывают глубокий смысл и пронизаны непостижимой магией.
И так, дорогие друзья, ведущие цифры этого удивительного путешествия – чудеса великой математики имеют название, которое звучит как чарующий приговор: "простые числа". Это избранные единицы, убежденные в собственной неповторимости, непревзойденности и непроницаемости. Они отличны от всех остальных, ибо они не делятся ни на какое другое число, кроме единицы и самих себя. Сегодня мы раскроем для вас олицетворение этого таинственного и загадочного числового господства, изучим его основы, обнаружим свойства и проникнем в мир примеров.
Уникальный раздел: Что подразумевается под понятием "неделимое число"?

В мире чисел существуют особые составные числа, которые нельзя поделить на меньшие числа, кроме единицы и самого себя. Эти особые числа имеют уникальные свойства, которые делают их основой для многих математических операций и разработки различных методов.
Такие числа, как "неделимые числа", "отличные от остальных чисел", "простые составные числа" и другие названия, используются для описания этой интересной группы чисел, столь важных в математике.
Одной из главных особенностей таких чисел является их неделимость нацело только на единицу и само число, что отличает их от остальных чисел. Простые числа можно назвать камнями-основаниями, на которых строятся все остальные числа.
Для простых чисел характерны такие свойства, как отсутствие делителей, кроме 1 и самого числа. Это означает, что в эту группу чисел попадают только те, которые являются "неделимыми" на наименьшее количество делителей.
В этом разделе мы рассмотрим подробнее, что такое простые числа и почему их изучение является важным в математике.
Изучаем основные концепции

Особым вниманием будут объяснены ключевые принципы и связи, позволяющие понять сущность и значение простых чисел. Кроме того, мы рассмотрим несколько примеров и акцентируем внимание на основных свойствах, которые делают простые числа уникальными в мире математики.
В процессе изучения этого раздела, вы получите фундаментальные знания, а также научитесь распознавать и анализировать простые числа в различных ситуациях. Разберетесь с закономерностями и прокатитесь по "простому" пути знаний в этой невероятной математической области.
Уникальный раздел: Специфические характеристики простых чисел
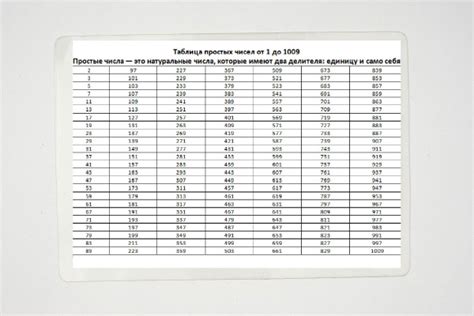
Уникальные свойства
Изучение свойств простых чисел в математике 6 класса позволяет обнаружить множество интересных особенностей в их структуре. Сегодня мы сосредоточимся на специфических характеристиках простых чисел, которые делают их настолько уникальными в мире чисел.
Определение простых чисел
Прежде чем войти в детали, давайте освежим память. Простые числа - это числа, которые имеют только два делителя: единицу и само число. Они не делятся ни на какие другие числа, за исключением самих себя и единицы.
Однозначность разложения на простые множители
Самое удивительное свойство простых чисел - их способность быть "конечной гранью" для всех натуральных чисел. Каждое натуральное число может быть представлено как произведение простых чисел в единственном порядке. Это называется однозначностью разложения на простые множители и является фундаментальной особенностью простых чисел.
Бесконечность простых чисел
Одной из самых захватывающих особенностей простых чисел является их бесконечность. Независимо от того, какой диапазон чисел мы рассматриваем, всегда найдется новое простое число, не являющееся произведением или делителем других чисел в этом диапазоне. Это делает простые числа особенно важными и интригующими для математиков.
Простые числа и криптография
Помимо своих математических свойств, простые числа играют важную роль в области криптографии. Их специфические характеристики делают их незаменимыми для защиты информации и шифрования данных. Понимание свойств простых чисел помогает создавать надежные системы шифрования и обеспечивать безопасность в современном цифровом мире.
Заключение
Свойства простых чисел - это не только увлекательный объект исследований в математике, но и фундаментальные понятия, которые пронизывают множество аспектов нашей жизни. Хотя мы только коснулись поверхности их уникальных характеристик, каждый шаг в изучении простых чисел открывает новые горизонты понимания и интригует наш разум.
Что отличает простые числа?

Одно из главных отличий простых чисел заключается в их неразложимости на множители. Простые числа представляют собой числа, которые не имеют делителей, кроме самих себя и единицы. Это свойство делает их неподвластными разложению на множители других чисел. Таким образом, простые числа не могут быть представлены в виде произведения других чисел и являются непосредственными строительными блоками для составления более сложных чисел.
Кроме непревзойденной уникальности, простые числа обладают также симметрией, которая их выделяет. В свойствах простых чисел отражается их равноправие и равномерное распределение, что делает их еще более привлекательными для исследования и использования в математических моделях.
Простые числа играют важную роль в теории чисел и находят применение в различных областях науки и техники. Они помогают решать сложные задачи, связанные с шифрованием, факторизацией и определением простоты больших чисел. Без понимания и изучения простых чисел невозможно представить себе современные достижения науки и технологии.
Как определить число, которое имеет только два собственных делителя?

Есть способ определить числа, которые не делятся нацело ни на одно число, кроме единицы и самого себя. Эти числа называются простыми числами.
Определение простого числа основывается на том, что такое число должно иметь только два собственных делителя. Другими словами, простое число не делится ни на одно другое натуральное число кроме единицы и самого себя.
Чтобы определить, является ли число простым, можно проверить, делится ли оно на любое натуральное число в диапазоне от 2 до его квадратного корня. Если при проверке число делится хотя бы на одно число из этого диапазона, то оно не является простым. Если же число не делится ни на одно из этих чисел, то оно простое.
Например, чтобы проверить, является ли число 17 простым, нужно проверить, делится ли оно на числа от 2 до 4, так как квадратный корень из 17 округленно равен 4.12. Если число 17 не делится ни на одно из этих чисел, значит, оно является простым.
Таким образом, определить простое число можно с помощью проверки деления на натуральные числа от 2 до квадратного корня из этого числа.
Методы проверки и примеры
В данном разделе рассмотрим различные методы, которые позволяют определить особые свойства чисел, а также приведем примеры, иллюстрирующие применение этих методов.
- Проверка на делимость. Для определения простоты числа можно применить метод проверки на делимость, который заключается в поиске делителей числа. Если число имеет делители, кроме 1 и самого себя, оно не является простым.
- Решето Эратосфена. Этот метод основан на пошаговом отсеивании составных чисел. Путем последовательного зачеркивания всех чисел, начиная с 2, мы оставляем только простые числа.
- Тест Миллера-Рабина. Этот вероятностный алгоритм позволяет определить, является ли число простым или составным. Он основан на рандомизированном выборе чисел и проверке некоторых свойств.
Приведем несколько примеров для наглядности:
- Проверим число 17 на простоту. Применяя метод проверки на делимость, мы увидим, что число 17 не имеет делителей, кроме 1 и самого себя, поэтому оно является простым.
- Применим Решето Эратосфена к последовательности чисел от 1 до 30. После применения этого метода, мы найдем все простые числа в данной последовательности, такие как 2, 3, 5, 7, 11, 13, 17, 19, 23 и 29.
- Применим тест Миллера-Рабина к числу 91. Этот метод позволяет нам убедиться, что число 91 составное, так как оно не проходит некоторые проверки на простоту.
Используя эти методы и примеры, можно более подробно изучить основные свойства простых чисел и научиться применять их на практике.
Вопрос-ответ

Какие свойства имеют простые числа?
Простые числа являются натуральными числами, которые больше единицы и имеют только два делителя: единицу и само число. Они не делятся ни на одно другое число, кроме единицы и самого себя. Также, любое натуральное число можно представить в виде произведения простых чисел (факторизация).
Как определить, является ли число простым или составным?
Для определения, является ли число простым или составным, необходимо проверить, делится ли оно на какое-либо другое число, не равное единице и самому себе. Если число делится, то оно является составным, если не делится, то оно простое.
Какие примеры простых чисел можно привести?
Примеры простых чисел включают 2, 3, 5, 7, 11, 13, 17, 19 и так далее. Простых чисел бесконечно много.
Зачем изучать простые числа в 6 классе?
Изучение простых чисел в 6 классе является важным этапом математического образования, так как понимание их основ и свойств помогает развить логическое мышление, умение делить числа и факторизировать их, а также позволяет лучше понять дроби, десятичные исчисления и другие математические концепции.
Можно ли использовать простые числа для шифрования информации?
Да, простые числа широко применяются в криптографии и шифровании информации. Например, алгоритм RSA, основанный на факторизации больших простых чисел, используется для защиты данных в банках, интернет-трафика, электронной почты и других системах, требующих безопасности.



