Разбор матрицы 4x4 – это глубокое исследование, открытие ее существенных свойств и закономерностей. Понимание ключевых моментов и особенностей структуры матрицы дают возможность эффективно решать задачи обратной матрицы, находить решения систем линейных уравнений, а также выявлять важные величины, вроде определителя, без внутреннего участия сложных алгоритмов.
Более пристальное рассмотрение структуры и специфики матрицы 4x4 раскрывает глубину и интерес применения этого математического инструмента. В практике различных областей, включая физику, экономику, инженерию и информатику, то есть там, где речь идет о линейных уравнениях, задачи на нахождение обратной матрицы и калибровке технических систем, активно используется матрица 4х4.
В данной статье будут представлены несколько очень удобных и элегантных способов вычисления определителя матрицы 4x4. Вы сможете узнать, как применить методы линейной алгебры для вычисления данной ключевой величины, познакомиться с их основными принципами и правилами применения, а также изучить конкретные примеры для наглядного представления процесса вычисления. Благодаря этим методам и примерам, у вас будет возможность увидеть в матрице не просто набор чисел, а целый мир ваших возможностей!
Метод Гаусса: нахождение определителя 4x4 матрицы

Процесс применения метода Гаусса для нахождения определителя 4x4 матрицы включает несколько шагов. Сначала матрица приводится к ступенчатому виду: каждая последующая строка умножается на определенный множитель и вычитается из предыдущих строк, чтобы все элементы ниже главной диагонали стали равными нулю. Затем определитель вычисляется как произведение диагональных элементов ступенчатой матрицы, с учетом знаков множителей, которые были использованы в процессе приведения матрицы к ступенчатому виду.
Метод Гаусса является эффективным способом вычисления определителя 4x4 матрицы и позволяет избежать применения прямого метода, который требовал бы больше времени и вычислительных ресурсов. Этот метод может быть использован для нахождения определителя в различных приложениях, включая обработку данных, анализ систем линейных уравнений и решение задач из физики и экономики.
Описание и принцип работы метода Гаусса
Идея метода Гаусса состоит в последовательном приведении матрицы к ступенчатому виду, при котором все элементы под главной диагональю обнуляются. Это достигается путем комбинации элементарных преобразований: вычитания одной строки из другой, умножения строки на ненулевое число и перестановки строк местами.
Применение метода Гаусса позволяет упростить систему линейных уравнений и найти ее решение. Ступенчатый вид матрицы позволяет выразить все переменные от последних к первым, приводя систему к треугольной матрице, в которой решение задачи становится очевидным.
Однако, при работе с матрицами, которые содержат нулевые строки или повторяющиеся строки, метод Гаусса может столкнуться с трудностями. В таких случаях требуется использовать дополнительные преобразования и методы для получения более общего решения системы уравнений.
Алгоритм определения значения через метод Гаусса
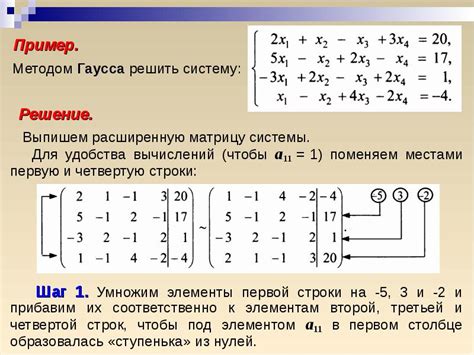
Вычисление значения определителя матрицы размером 4 на 4 может быть осуществлено с помощью метода Гаусса, который позволяет сократить сложность вычислений путем приведения исходной матрицы к треугольному виду. Этот алгоритм представляет собой последовательность элементарных преобразований, в результате которых определитель принимает треугольную форму. После этого, произведение элементов главной диагонали треугольной матрицы даст искомое значение определителя.
Основная идея метода Гаусса заключается в использовании элементарных преобразований над исходной матрицей для приведения ее к упрощенному виду. Эти преобразования включают в себя перестановку строк, умножение строк на число и сложение строк с учетом определенных правил. Применение преобразований делает матрицу триангулярной, то есть все элементы ниже главной диагонали равны нулю.
| A | B | C | D |
| E | F | G | H |
| I | J | K | L |
| M | N | O | P |
Для примера, рассмотрим матрицу размером 4 на 4, представленную выше. Сначала применяются элементарные преобразования для обнуления элементов ниже главной диагонали в первом столбце. На следующем шаге обнуляются элементы, находящиеся ниже главной диагонали во втором столбце, и так далее. После проведения всех преобразований получаем треугольную матрицу:
| A' | B' | C' | D' |
| 0 | F' | G' | H' |
| 0 | 0 | K' | L' |
| 0 | 0 | 0 | P' |
Искомое значение определителя матрицы равно произведению элементов главной диагонали треугольной матрицы:
определитель = A' * F' * K' * P'
Метод разложения по столбцу для определителя 4x4

Один из эффективных методов вычисления определителя 4x4 матрицы предполагает разложение матрицы по столбцу. Этот метод основывается на представлении матрицы в виде суммы произведений элементов столбца на их соответствующие алгебраические дополнения. Определитель вычисляется путем сложения значений полученных произведений с разными знаками. Такой подход позволяет существенно упростить и ускорить процесс вычисления определителя 4x4 матрицы.
Для примера, рассмотрим следующую матрицу:
| a | b | c | |
| d | e | f | |
| g | h | i | |
| j | k | l |
Для вычисления определителя данной матрицы, мы выбираем один из столбцов (например, первый столбец) и разлагаем его на элементы: a, d, g и j. Затем, для каждого элемента, вычисляем его алгебраическое дополнение и умножаем его на соответствующий элемент столбца. Полученные произведения суммируются с учетом знаков и дают нам значение определителя 4x4 матрицы.
Принцип работы метода разложения по столбцу

Разложение по столбцу предполагает выбор одного из столбцов исходной матрицы и дальнейшую рекурсивную обработку оставшихся элементов матрицы, исключая выбранный столбец и строку, содержащую элемент этого столбца.
Процесс разложения выполняется до тех пор, пока не достигнется матрица размером 2 на 2, для которой определитель можно вычислить непосредственно. Затем, на основе найденных определителей, производится последовательное обратное умножение элементов исходного столбца матрицы на их соответствующие определители подматриц. Результаты умножения суммируются, что позволяет получить значение определителя матрицы размером 4 на 4.
Метод разложения по столбцу представляет удобный подход к вычислению определителя матрицы 4 на 4, позволяющий существенно сократить вычислительную сложность и ускорить процесс вычисления, особенно при наличии программной реализации данного метода.
Алгоритм разложения по столбцу: вычисление определителя матрицы 4 на 4

В данном разделе мы рассмотрим алгоритм вычисления определителя матрицы размером 4 на 4 с использованием метода разложения по столбцу. Этот метод позволяет нам разложить матрицу на сумму произведений ее элементов таким образом, что каждое слагаемое содержит элементы только из одного столбца. Такой подход позволяет упростить вычисление определителя и сделать его более легким для понимания.
Первый шаг алгоритма заключается в выборе одного из четырех столбцов матрицы, по которому будем разлагать. Мы обозначим этот столбец как A, а оставшиеся три столбца как B, C и D. Затем мы разложим определитель матрицы на сумму трех определителей, которые будут получены путем вычеркивания строки и столбца, которые содержат выбранный столбец A.
Для вычисления каждого из трех определителей нам понадобится применить рекурсивный подход. Мы будем последовательно выбирать по одному элементу из столбцов B, C и D и умножать его на определитель матрицы, полученной вычеркиванием строки и столбца, в которых находится выбранный элемент. Затем мы будем суммировать полученные произведения и получим определитель матрицы размером 4 на 4.
Алгоритм вычисления определителя с помощью метода разложения по столбцу является эффективным и позволяет нам получить точный результат для матрицы размером 4 на 4 без необходимости выполнять множество сложных вычислений.
Свойства характеристик матриц 4 на 4: объединяющие закономерности и уникальные особенности
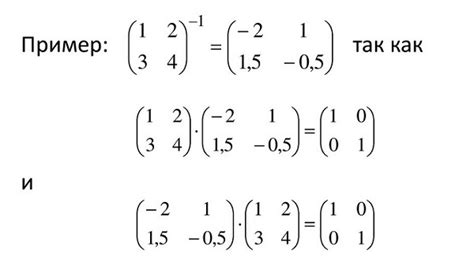
Раздел "Свойства характеристик матриц 4 на 4" представляет собой исследование общих характеристик и закономерностей определителей данного типа матриц. Эти свойства играют важную роль при анализе и решении математических задач, поскольку позволяют упростить и оптимизировать вычисления без использования конкретных методов и примеров вычисления определителей. Мы описываем уникальные особенности и взаимосвязи, которые помогут вам лучше понять и применять определители матриц 4 на 4 в различных контекстах.
Уникальные особенности: В данном разделе мы рассматриваем основные свойства определителей матриц 4 на 4, касающиеся их знакопостоянства, линейности и скалярного множителя. Мы анализируем, как знак определителя зависит от перестановок элементов матрицы и об относительной расположенности самих элементов. Особое внимание уделяется связи между определителями матрицы и ее собственными значениями, а также взаимодействию с другими характеристиками матриц, такими как след и трасса.
Объединяющие закономерности: В рамках данного раздела мы обсуждаем общие закономерности, которые применимы к определителям матриц 4 на 4. Рассматриваются такие свойства, как линейность относительно строк и/или столбцов матрицы, а также связь с другими алгебраическими операциями и свойствами матриц. Мы также предлагаем примеры, иллюстрирующие данные закономерности и помогающие лучше понять их важность и применимость.
В заключении нашего исследования мы надеемся, что данный раздел поможет вам более глубоко и уверенно владеть знаниями о свойствах определителей матриц 4 на 4. Это является важным шагом в освоении методов вычисления определителей и их применении в различных математических дисциплинах.
Сущность определителя матрицы 4 на 4 и его взаимосвязь с подматрицами
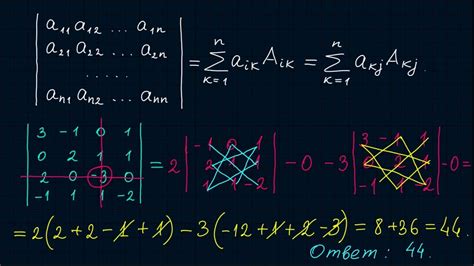
Определитель матрицы 4 на 4 представляет собой числовое значение, которое можно вычислить по определенным правилам. Он связан с подматрицами данной матрицы: изменение элементов конкретных подматриц влияет на значение определителя, и наоборот.
Подматрица является частью матрицы, образованной отбрасыванием некоторых строк и столбцов. Изменение элементов подматрицы может влиять на значение определителя матрицы 4 на 4, а изменение самого определителя может указывать на свойства и структуру подматрицы.
Понимание связи между определителем матрицы 4 на 4 и ее подматрицами позволяет создать эффективные методы решения задач линейной алгебры, оптимизировать вычисления и анализировать геометрическую интерпретацию матричных операций. При изучении этой связи становится ясным, почему некоторые подматрицы матриц 4 на 4 могут быть особыми или играть важную роль в конкретных задачах.
Вопрос-ответ

Определить матрицу 4 на 4 - как это делается?
Чтобы определить матрицу 4 на 4, необходимо вычислить её определитель. Для этого можно использовать различные методы, такие как правило Саррюса, разложение по строке или столбцу, или методы приведения к верхнетреугольному или диагональному виду. Выбор метода зависит от конкретной матрицы. Далее, полученный определитель можно использовать для решения задач, связанных с системами линейных уравнений, вычислением площади или объёма, проверки линейной зависимости и т.д.
Как вычислить определитель матрицы 4 на 4 методом разложения по строке?
Для вычисления определителя матрицы 4 на 4 методом разложения по строке необходимо выбрать одну из строк и разложить определитель по этой строке в сумму произведений элементов матрицы на их алгебраические дополнения. Затем выполнить аналогичные действия для остальных строк и сложить полученные произведения с правильными знаками. Для примера, если выбирается первая строка, то ищется определитель 3 на 3, который также можно вычислить методом разложения по строке или столбцу. Полученные значения умножаются на элементы первой строки матрицы и складываются с правильными знаками.
Назовите примеры задач, в которых определитель матрицы 4 на 4 может использоваться.
Определитель матрицы 4 на 4 может быть полезен при решении систем линейных уравнений с четырьмя неизвестными, так как он связан с существованием и единственностью решений таких систем. Также, определитель может использоваться для вычисления площади параллелограмма, построенного на векторах, задаваемых столбцами матрицы 4 на 4. Определитель может помочь также в проверке линейной зависимости четырёх векторов, задаваемых столбцами матрицы.
Какой метод наиболее эффективен для вычисления определителя матрицы 4 на 4?
Для матриц 4 на 4 нет строго наиболее эффективного метода вычисления определителя. Используемый метод зависит от конкретной матрицы и её особенностей. Например, метод Саррюса может быть удобен, если матрица имеет много нулевых элементов, а метод разложения по строке может быть эффективен, если одна из строк содержит много нулевых элементов. Часто используются методы приведения к верхнетреугольному или диагональному виду, которые позволяют сократить количество операций для вычисления определителя.



