Существует одно захватывающее явление, которое мы наблюдаем в окружающем нас мире: все вокруг нас имеет форму. От капли дождя до круглых лиц, от конусообразных льдиных гор до снежинок – формы окружают нас повсюду. И центральной из этих форм, символизирующей гармонию и совершенство фигур, является окружность.
Однако, когда речь заходит о важных характеристиках окружности, таких как длина окружности, вопросы и сомнения охватывают большинство из нас. Но не стоит отчаиваться! Мы нашли ключ к разгадке, который позволит вам вычислить длину окружности без особых усилий и сложных формул.
Таким ключом являются два понятия, без которых невозможно представить себе геометрию и связь размеров колец наших жизней: диаметр и радиус. Эти два термина являются основными строительными блоками окружности и помогут нам разгадать загадку ее длины. Величина диаметра окружности устанавливает ее размер и ширину, в то время как радиус отражает расстояние от центра до любой точки на окружности.
Значение длины окружности в геометрии: основные понятия и применение
Одним из ключевых понятий, связанных с окружностью, является ее длина. Длина окружности – это расстояние, которое нужно пройти вдоль границы окружности, чтобы вернуться в исходную точку. Зная значение длины окружности, мы можем более точно описать и изучать эту фигуру.
Знание длины окружности имеет множество применений в различных областях. В архитектуре и инженерии, зная длину окружности, мы можем рассчитывать необходимое количество материалов для построения и создания круглых структур. В физике и астрономии, знание длины окружности помогает расчетам и предсказанию движения тел в круговых орбитах. Даже в повседневной жизни, зная длину окружности, мы можем сделать математически обоснованные оценки и измерения.
Понятие окружности и основные свойства
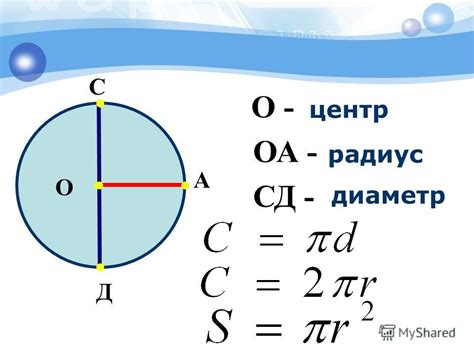
Диаметр – это отрезок, соединяющий две точки на окружности и проходящий через ее центр. Если обозначить длину диаметра как D, то он является самой длинной прямой линией, которая может быть нарисована внутри окружности.
Радиус – это половина диаметра окружности. Обычно обозначается символом r. Радиус является мерой расстояния от центра окружности до любой точки на ней.
Центр – это фиксированная точка, от которой все точки окружности находятся на одинаковом расстоянии. Отмечается обычно символом O или C.
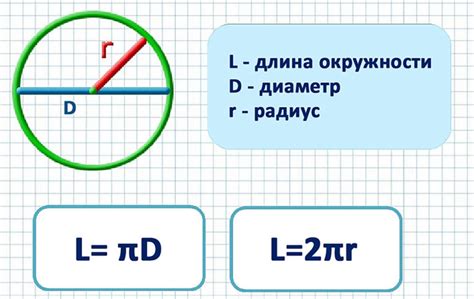
Длина окружности – это периметр окружности, то есть общая длина внешней границы окружности. Она измеряется в единицах длины, таких как метры или сантиметры, и зависит от диаметра или радиуса окружности.
Изучение понятия окружности и ее основных характеристик позволяет не только лучше понять ее геометрическую природу, но и решать различные задачи, связанные с вычислением ее длины, площади и других значений.
Значение длины окружности в повседневной жизни и научных областях
В повседневной жизни и научных областях длина окружности играет важную роль, исследуя ее значения мы можем расширить наше понимание мира и применить это знание в различных сферах деятельности. Длина окружности во многом определяет форму и размеры объектов, а также может быть использована для оценки расстояний и прогнозирования их перемещений.
В архитектуре и дизайне длина окружности позволяет создавать идеально сбалансированные и пропорциональные формы зданий и конструкций. Размеры окружности являются основным параметром при разработке мостов, арок и куполов, где точность вычислений необходима для обеспечения стабильности и безопасности сооружений.
В физике и инженерии знание длины окружности позволяет изучать и моделировать различные движения и процессы. Например, при проектировании колесных систем и передач определенное значение окружности используется для расчета передаточного числа и скорости передвижения. Также длина окружности имеет важное значение при изучении электрических цепей и синусоидальных колебаний.
В астрономии и навигации длина окружности помогает определить координаты и проложить маршруты. Например, для вычисления широты и долготы на планете Земля используются значения длины окружности, а для навигации в космосе она позволяет рассчитывать траектории полетов и межпланетные расстояния.
Таким образом, понимание значения длины окружности в повседневной жизни и научных областях помогает нам более глубоко исследовать и объяснять множество процессов и закономерностей, а также применять полученные знания для решения различных задач и создания новых технологий.
Определение диаметра окружности и его связь с протяженностью окружности

В предыдущих разделах мы рассмотрели способы нахождения длины окружности по ее диаметру. Однако, чтобы более глубоко понять суть этой формулы и ее применение, важно разобраться в понятии диаметра и его связи с протяженностью окружности.
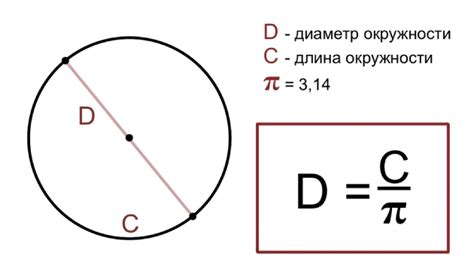
Диаметр окружности - это отрезок, соединяющий две точки на окружности и проходящий через ее центр. Он является наибольшим прямым отрезком, который можно построить внутри окружности. Для расчета длины окружности, которая представляет собой измерение протяженности окружности, мы используем диаметр.
Связь между диаметром и длиной окружности выражается через известное математическое соотношение. Зная диаметр, мы можем найти длину окружности, а зная длину окружности, мы можем вычислить диаметр. Эта связь основана на числе "пи" (π), которое приближенно равно 3.14159.
В следующем разделе мы рассмотрим основные формулы для нахождения длины окружности и диаметра, а также подробнее рассмотрим их применение в практических задачах.
Диаметр окружности: понятие, свойства и примеры
- Определение диаметра:
- Диаметр - это отрезок, соединяющий две точки на окружности и проходящий через ее центр;
- Диаметр является наибольшей характеристикой окружности, определяемой его длиной;
- Диаметр можно рассматривать как две равные половины окружности.
- Свойства диаметра:
- Диаметр является осью симметрии окружности;
- Длина диаметра равна двум радиусам окружности;
- Диаметр является базовым элементом для расчета длины окружности.
- Примеры использования диаметра:
- В строительстве: определение диаметра основания столба, трубы или колонны;
- В инженерии: расчет диаметра шестерни в передаче;
- В геометрических задачах: определение диаметра орбиты планеты.
Знание о диаметре окружности является фундаментальным для практического применения геометрических принципов в решении различных задач. Уверенное владение этим понятием позволит использовать его в различных областях науки и техники.
Формула взаимосвязи диаметра окружности и ее протяженности
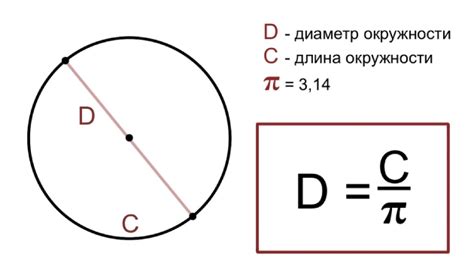
В рассматриваемом контексте мы изучаем закономерности, связывающие различные параметры окружности. Раздел "Формула связи диаметра окружности и ее длины" посвящен исследованию взаимосвязи между диаметром окружности и ее протяженностью.
Диаметр окружности – это один из основных параметров, определяющих ее форму и размеры. Этот параметр присутствует в различных формулах и уравнениях, позволяющих вычислять другие характеристики окружности. Интересное открытие заключается в том, что диаметр и длина окружности оказываются тесно связаны.
Формула связи диаметра и длины окружности, которую мы рассмотрим в данном разделе, позволяет определить длину окружности по заданному диаметру. Знание этой формулы может быть полезно в различных практических задачах, связанных с геометрией и строительством.
Эта формула позволяет получить точное значение длины окружности без необходимости измерения каждого отрезка по отдельности. Воспользуйтесь формулой связи диаметра окружности и ее длины, чтобы упростить расчеты и получить точные результаты в своих задачах.
Вопрос-ответ

Какая формула используется для нахождения длины окружности по диаметру?
Формула для нахождения длины окружности по диаметру - это L = π * d, где L обозначает длину окружности, а d - диаметр. Чтобы найти длину окружности, нужно умножить диаметр на число π (пи) , которое равно приблизительно 3,14159.
Есть ли другая формула, которую можно использовать для расчета длины окружности?
Да, существует еще одна формула для расчета длины окружности. Она выглядит так: L = 2 * π * r, где L - длина окружности, r - радиус. Радиус – это половина диаметра, поэтому можно также использовать эту формулу, зная только радиус и число π.
Какую точность можно достичь при расчете длины окружности?
При использовании формулы L = π * d и числа π, которое приблизительно равно 3,14159, точность расчета длины окружности будет зависеть от значений диаметра. Чем больше количество знаков после запятой используется в числе π, тем точнее будет расчет.
Можно ли использовать математический программный код для нахождения длины окружности?
Да, можно написать программный код на различных языках программирования, чтобы автоматически находить длину окружности. В большинстве языков программирования есть встроенная функция для нахождения значения числа π, и вычисление длины окружности по диаметру становится намного проще.
Для чего может понадобиться знание длины окружности по диаметру?
Знание длины окружности по диаметру может быть полезно в различных областях, таких как геометрия, строительство, инженерия и физика. Например, при проектировании круглых объектов, определении длины кабеля или трубы, расчете пути движения колеса или при описании законов физики, связанных с окружными движениями.
Что такое окружность?
Окружность - это геометрическая фигура, представляющая собой замкнутую кривую линию, все точки которой равноудалены от центра.



