Когда мы изучаем график функции, одним из важных аспектов становится понимание момента, когда он пересекает ось ординат. Такой пересечения обладает своей уникальностью и указывает на значимые значения функции. В данном разделе, мы сосредоточимся на рассмотрении различных методов и подходов, позволяющих установить положение точки пересечения с осью ординат без использования специальных терминов и определений.
Основная цель анализа точки пересечения с осью ординат состоит в выяснении, насколько функция отличается от нулевого значения в данном месте. Ведь эта точка может оказаться критической, играющей важную роль в определении характеристик функции. Для достижения этой цели, мы исследуем различные подходы, позволяющие различить позитивное и негативное положение точки на графике функции.
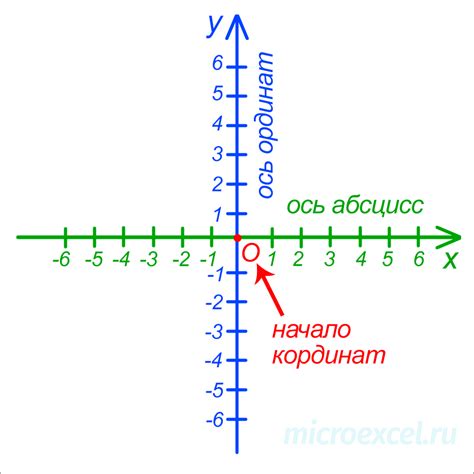
Понятие ординаты: путь к определению вертикальной координаты точки
В мире математики, для различных графиков и функций существует необходимость определить положение точек на вертикальной оси. В подобных случаях, мы ищем значение вертикальной координаты точки пересечения графика с осью ординат. В данном разделе мы рассмотрим различные способы определения понятия ординаты, изучим его значения и принципы вычисления, представленные разными математиками и учеными.
Что такое точка пересечения графика с осью ординат?
В данном разделе мы рассмотрим понятие точки пересечения графика функции с осью ординат и объясним, как она определяется и как ее можно найти. Эта точка играет важную роль в анализе функций и позволяет получить информацию о поведении функции при отсутствии аргумента.
Точка пересечения графика функции с осью ординат - это точка, в которой график функции пересекает ось ординат или вертикальную ось на координатной плоскости. В данной точке значение абсциссы (х-координаты) равно нулю, а ординаты (у-координаты) может быть любым числом. Математически, точка пересечения с осью ординат имеет координаты (0, y), где y - значение функции в данной точке.
Существует несколько способов нахождения точки пересечения графика функции с осью ординат. Во-первых, можно использовать графический метод. Для этого необходимо построить график функции на координатной плоскости и определить точку, в которой график пересекает ось ординат.
Второй способ - аналитический подход. Для этого необходимо решить уравнение функции, приравняв значение абсциссы к нулю. Полученное решение будет являться ординатой точки пересечения. Например, для функции y = 2x - 3 точка пересечения с осью ординат будет иметь координаты (0, -3).
Также стоит отметить, что существуют функции, которые не пересекают ось ординат. В таком случае говорят, что у функции нет точки пересечения с осью ординат или она пересекает ее в бесконечности.
- Точка пересечения графика с осью ординат - ключевой элемент анализа функций.
- Она представляет собой точку, в которой график функции пересекает ось ординат.
- Ее значение абсциссы равно нулю, а ординаты может быть любым числом.
- Поиск точки пересечения можно выполнить как графически, так и аналитически.
Связь между вертикальным положением точки пересечения графика функции и значением самой функции
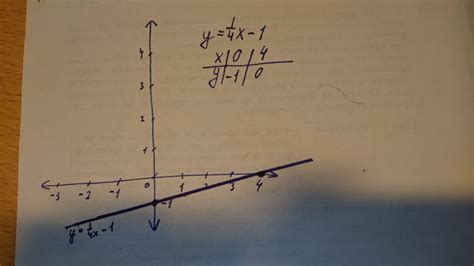
Значение функции в точке пересечения с вертикальной осью является ключевым показателем, поскольку оно указывает на соответствующую высоту графика в этой точке. Если значение функции положительное, то это означает, что график находится выше оси, а если оно отрицательное - график находится ниже оси. Поэтому значение функции в точке пересечения с вертикальной осью может помочь нам определить положение графика в отношении этой оси.
Помимо этого, значение функции в точке пересечения может также быть связано с конкретным значением, которое требуется найти при решении уравнения или задачи. Изучение графика функции и его пересечения с вертикальной осью позволяет нам найти такие значения и использовать их в дальнейшем анализе или при выполнении задач.
Метод графической определенной точки вертикального пересечения

Решение задачи нахождения значения ординаты точки пересечения графика функции с осью ординат можно осуществить с использованием графического метода. Этот метод позволяет визуально определить координаты пересечения графика функции с осью ординат, не прибегая к аналитическим вычислениям.
Суть метода заключается в следующем. Необходимо построить график функции на координатной плоскости и визуально найти точку, где этот график пересекает ось ординат. Для этого следует найти точку, где график функции пересекает ось абсцисс (ось x) и отметить ее на графике. Затем, проведя вертикальную линию из этой точки, можно определить точку пересечения графика функции с осью ординат. Координата этой точки и будет искомой ординатой точки пересечения.
При использовании графического метода следует обратить внимание на масштаб по осям координатной плоскости и точность проведения линий. Чем точнее и аккуратнее будет построен график и проведена вертикальная линия, тем более точными будут полученные результаты. Метод графического определения ординаты точки пересечения позволяет наглядно представить себе геометрическую суть этого процесса без использования сложных формул и вычислений.
| Преимущества метода | Недостатки метода |
| Простота и понятность выполнения | Определение ординаты точки с ограниченной точностью |
| Возможность наглядного представления результатов | Зависимость точности от качества построения графика |
| Отсутствие необходимости в аналитических расчетах |
Алгебраический способ нахождения вертикального положения точки пересечения
В данном разделе рассмотрим алгебраический подход к определению вертикального положения точки пересечения графика функции с осью ординат. Используя алгебраические методы, мы сможем определить координату точки пересечения, не прибегая к построению графика функции.
Для начала, воспользуемся алгебраическими свойствами выпуклости и вогнутости функции, а также знаками выражения, чтобы определить с какой стороны оси ординат функция пересекает.
Затем, мы можем применить методы решения уравнений, например метод подстановки или метод исключения, чтобы найти значение переменной, соответствующее точке пересечения. Это позволит нам определить ординату точки пересечения графика функции с осью ординат.
Важно отметить, что алгебраический метод нахождения ординаты точки пересечения может быть применен к любой функции, не зависимо от ее виду или сложности. Это делает его универсальным инструментом при анализе графиков функций.
- Использование алгебраических свойств функции
- Применение методов решения уравнений
- Универсальность алгебраического метода
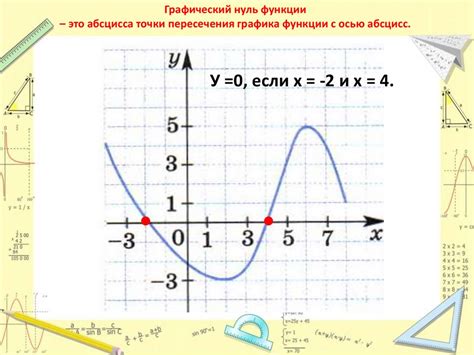
Примеры определения значения, где график пересекает ось ординат
В данном разделе рассмотрим несколько иллюстративных примеров, демонстрирующих различные способы нахождения точек пересечения графика с осью ординат. Будут рассмотрены как простые, так и сложные случаи, позволяющие наглядно представить основные концепции и методы решения данной задачи.
- Пример 1: Решение уравнения. Рассмотрим функцию y = 2x + 3. Для нахождения точки пересечения с осью ординат необходимо приравнять значение функции к нулю и решить полученное уравнение. В данном случае, приравниваем y = 0 и получаем уравнение 2x + 3 = 0. Далее, решаем его и находим значение x, которое будет ординатой искомой точки пересечения.
- Пример 2: Графическое представление. Возьмем функцию f(x) = sin(x). Чтобы найти точку пересечения графика с осью ординат, нам необходимо построить график данной функции и найти точку, в которой график пересекает ось ординат. Этот метод особенно полезен при анализе более сложных функций, где аналитическое решение может быть трудным.
- Пример 3: Применение теоремы Безу. Рассмотрим функцию f(x) = x^3 - 4x + 2. Используя теорему Безу, можем сказать, что ордината точки пересечения графика с осью ординат равна нулю, если коэффициент при x в данной функции равен 0. В данном случае, решаем уравнение x^3 - 4x + 2 = 0 и находим все корни. Затем, проверяем, при каком значении x функция обращается в 0, и это значение и будет ординатой искомой точки пересечения.
Приведенные примеры показывают различные подходы для нахождения ординаты точек пересечения графиков функций с осью ординат. Выбор метода зависит от конкретной функции и условий задачи. Знание и применение этих методов позволяет более глубоко изучить основы математического анализа и решать различные задачи в этой области.
Импортанс знаний об ординатном проектировании для анализа кривых функциональных линий
Способность понимать и интерпретировать ординатное размещение точки пересечения графика функции с осью абсцисс играет важную роль в анализе различных типов функциональных зависимостей. Каждый график может содержать ценную информацию, которая может быть использована для изучения характеристик и поведения функции в данной области.
Наблюдение и изучение ординатной координаты точки пересечения помогает выявить различные паттерны и тренды, которые могут быть полезными при прогнозировании и понимании функции. Ординатное размещение может указывать на возможные экстремумы, асимптотическое поведение или другие особенности графика функции.
Понимание значимости ординатного проектирования особенно полезно при выполнении сравнительного анализа различных функций и их графиков. Сравнение ординатных значений для нескольких точек пересечения может помочь определить, какая функция имеет более выраженные экстремумы, какая функция быстрее или медленнее меняется в зависимости от изменения аргумента, и т.д.
Знание ординат точек пересечения также может быть полезно при решении уравнений и систем уравнений, связанных с заданными функциями. Ординатные значения могут использоваться для проверки правильности решения и оценки точности результата. Они также могут помочь выявить проблемы и ошибки в алгоритмах решения.
В целом, понимание ординатного проектирования и умение анализировать размещение точек пересечения графиков функций с осью абсцисс способствует более глубокому пониманию функциональных зависимостей и поведения математических моделей, что может быть полезным в различных областях, включая науку, инженерию, экономику и другие.
Практическое применение знания об угловых коэффициентах Графика Показателя с осью абсцисс
Применение этого знания может быть полезным, например, для анализа рынка ценных бумаг. Зная угловой коэффициент графика изменения цен акций определенной компании, мы можем предположить, как цены будут меняться в будущем и принять решение о покупке или продаже акций. Также, это знание может быть полезным для оценки тенденций в экономике, прогнозирования роста или падения ВВП, анализа финансовых показателей различных отраслей.
Кроме того, знание об угловом коэффициенте и графике показателя может быть полезным в области маркетинга и продаж. Рассмотрим ситуацию, где у нас есть график роста продаж товара в зависимости от изменения рекламного бюджета. Зная угловой коэффициент графика, мы можем оценить эффективность вложений в рекламу и принять решение о дальнейших действиях в отношении рекламной кампании. Также, это знание может помочь в определении оптимального бюджета для маркетинговых мероприятий и позволит сократить расходы на нерентабельные виды рекламы.
Таким образом, понимание и применение знания об угловых коэффициентах графика показателя с осью абсцисс имеет широкие возможности в различных сферах деятельности. Оно позволяет нам анализировать и прогнозировать различные явления, принимать обоснованные решения и сокращать издержки в процессе принятия маркетинговых и финансовых решений.
Вопрос-ответ

Как найти ординату точки пересечения графика функции с осью ординат?
Ордината точки пересечения графика функции с осью ординат может быть найдена путем решения уравнения функции, где аргумент (абсцисса) принимает значение нуль. Если уравнение имеет вид y = f(x), то для нахождения ординаты точки пересечения с осью ординат подставляем x = 0 в уравнение и находим значение y.
Есть ли другой способ найти ординату точки пересечения графика функции с осью ординат, кроме решения уравнения?
Да, существует и другой способ нахождения ординаты точки пересечения с осью ординат. Если график функции является симметричным относительно оси ординат, то ордината точки пересечения будет равна нулю. Однако этот способ применим только в случае симметричности графика.
Можно ли найти ординату точки пересечения графика функции с осью ординат, если уравнение функции не дано?
Да, возможно найти ординату точки пересечения графика функции с осью ординат, даже если уравнение функции не известно. Для этого необходимо проанализировать график и определить точку, где он пересекает ось ординат. Затем можно измерить значение ординаты этой точки на оси координат.



