Интуитивно понятно, что точка может находиться либо внутри треугольника, либо за его пределами. Однако, когда речь идет о проверке формальной принадлежности точки треугольнику, возникает необходимость применить определенные математические алгоритмы и методы. В данной статье мы рассмотрим несложный и эффективный способ определить, принадлежит ли заданная точка треугольнику, без необходимости проведения длительных вычислений или использования сложных формул.
Для решения этой задачи существует несколько подходов. Один из них основан на использовании площадей треугольников. Однако, для его понимания и применения необходимо быть знакомым с определениями понятий, таких как векторы, скалярное произведение и координаты. Другой метод, который мы рассмотрим, основан на использовании барицентрических координат, позволяющих представить заданную точку как сумму весовых коэффициентов положения трех вершин треугольника. Этот способ нагляден, понятен и не требует глубоких знаний математики для его применения.
Необходимо отметить, что проверка принадлежности точки треугольнику является важной задачей в геометрии и находит свое применение в различных областях. Например, при работе с графиками или при определении положения объектов в трехмерном пространстве. Кроме того, знание и понимание этого метода может быть полезным для тех, кто интересуется математикой и геометрией.
Определение положения точки относительно треугольника
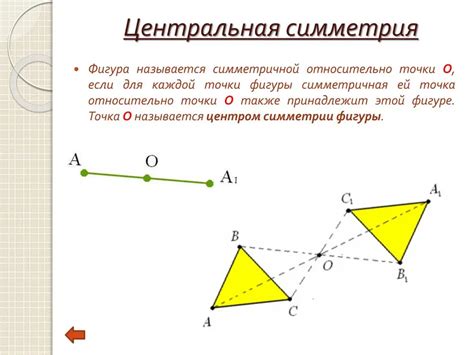
Имея треугольник и точку, иногда необходимо определить, находится ли эта точка внутри треугольника или вне его. Решение этой задачи может быть полезным, например, при работе с географическими данными, графиками или визуализации данных.
Существует несколько методов, которые позволяют определить принадлежность точки треугольнику. Один из них основан на анализе площадей подтреугольников, образованных точкой и сторонами треугольника. Другой метод использует векторные вычисления для определения положения точки относительно треугольника.
Одним из наиболее понятных методов является "метод пересечения отрезков". По сути, этот метод сводится к проверке пересечения прямых, которые образуют стороны треугольника, с другой прямой, проходящей через данную точку. Если все пересечения происходят по одну сторону от точки, то она будет находиться внутри треугольника. В противном случае, точка будет находиться снаружи треугольника.
Знание и понимание таких методов позволит более точно анализировать и обрабатывать данные, связанные с принадлежностью точки треугольнику, и применять полученную информацию в различных задачах и проектах.
Метод определения принадлежности точки треугольнику на основе координат
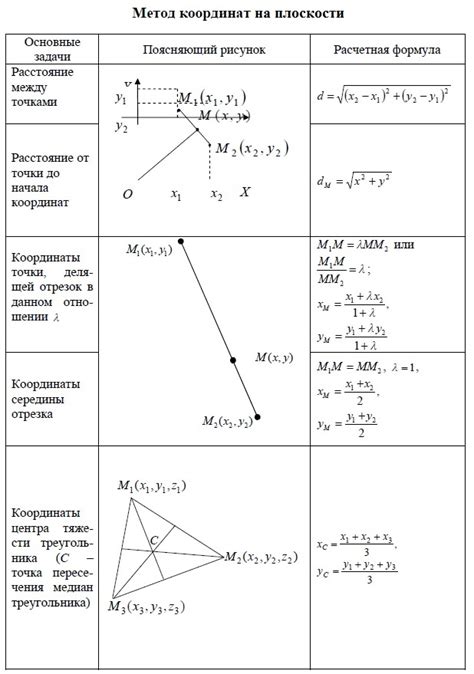
Для определения принадлежности точки треугольнику можно использовать метод, основанный на анализе координат точек. Данный подход позволяет определить, находится ли точка внутри треугольника или на его границе.
Для начала, необходимо задать координаты вершин треугольника и координаты проверяемой точки. Затем, используя алгоритм геометрических вычислений, можно определить расположение точки относительно треугольника.
- Шаг 1: С помощью векторных вычислений найдите векторы, соединяющие вершины треугольника.
- Шаг 2: Затем найдите векторы, соединяющие вершины треугольника с проверяемой точкой.
- Шаг 3: После этого, проанализируйте знаки двухпересекающихся векторов: если они совпадают, то точка находится внутри треугольника, если различаются, то точка находится снаружи треугольника.
Таким образом, метод координат точек основывается на использовании геометрических вычислений и анализе знаков векторов. Этот подход позволяет быстро и эффективно определить принадлежность точки треугольнику без необходимости в сложных математических выкладках.
Метод определения принадлежности точки треугольнику с помощью угловых коэффициентов прямых
Для реализации этого метода необходимо определить угловые коэффициенты каждой из сторон треугольника и сравнить их с угловыми коэффициентами прямых, проведенных через данную точку. Угловой коэффициент прямой определяется как отношение разности координат по оси Y к разности координат по оси X.
Точка будет принадлежать треугольнику, если выполнены следующие условия: все угловые коэффициенты прямых, проведенных через данную точку и вершины треугольника, будут одинаковыми; сумма углов треугольника, образованных точкой и двумя его вершинами, равна 180 градусам.
Метод угловых коэффициентов прямых позволяет эффективно определить, находится ли точка внутри треугольника или на его границе, что может быть полезным в различных геометрических расчетах и применениях.
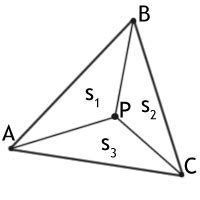
Метод вычисления площадей треугольников в контексте определения принадлежности точки
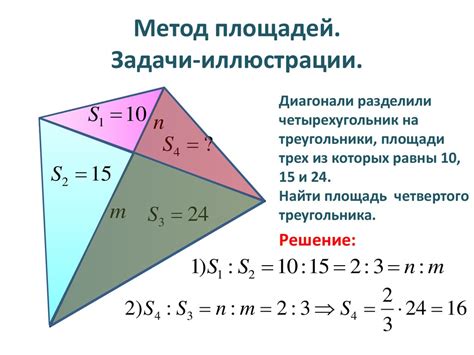
В этом разделе будет рассмотрен метод определения принадлежности точки треугольнику с использованием площадей.
При решении задачи о проверке принадлежности точки треугольнику можно воспользоваться методом, основанным на вычислении площадей треугольников. Этот метод позволяет определить, находится ли точка внутри треугольника или на его границе.
Для начала необходимо вычислить площадь самого треугольника и площади трех треугольников, образованных точкой и сторонами исходного треугольника. Затем сравнение площадей даст ответ о принадлежности точки треугольнику.
Если сумма площадей трех треугольников образованных точкой и сторонами исходного треугольника равна площади всего треугольника, то точка находится внутри треугольника. В противном случае точка находится или на одной из сторон треугольника или за его пределами.
Такой метод применяется в различных областях, например, в геометрии, компьютерной графике и геоинформационных системах. Изучение этого метода позволяет развить навыки работы с площадями и треугольниками, а также применить их для решения практических задач, связанных с определением принадлежности точек треугольнику.
Вопрос-ответ

Как проверить принадлежность точки треугольнику?
Для проверки принадлежности точки треугольнику можно использовать метод площадей. Сначала находим площади трех треугольников, образованных данной точкой и вершинами исходного треугольника. Затем суммируем эти площади и сравниваем полученное значение с площадью исходного треугольника. Если сумма площадей внутренних треугольников равна площади исходного треугольника, то точка принадлежит ему. Если же сумма площадей меньше или больше площади исходного треугольника, то точка находится вне треугольника.
Как использовать метод площадей для проверки принадлежности точки треугольнику?
Чтобы использовать метод площадей для проверки принадлежности точки треугольнику, нужно определить площади трех треугольников, образованных данной точкой и вершинами исходного треугольника. Для этого можно воспользоваться формулой герона, которая позволяет найти площадь треугольника по длинам его сторон. Затем суммируем полученные площади и сравниваем с площадью исходного треугольника. Если они равны, то точка принадлежит треугольнику. Если не равны, то точка находится вне треугольника.
Какие есть другие способы проверки принадлежности точки треугольнику, кроме метода площадей?
Помимо метода площадей, существуют и другие способы проверки принадлежности точки треугольнику. Один из них - это использование уравнений прямых, проходящих через стороны треугольника. Другой способ основан на нахождении барицентрических координат точки относительно вершин треугольника. Также можно использовать метод расщепления треугольника на три подтреугольника и проверки принадлежности точки каждому из них. Каждый из этих методов имеет свои особенности и может быть использован в зависимости от задачи.
Какие условия должны быть выполнены для применения метода площадей в проверке принадлежности точки треугольнику?
Для применения метода площадей в проверке принадлежности точки треугольнику необходимо, чтобы все три вершины треугольника были попарно различными. Если две или три вершины совпадают, то площади треугольников будут равны нулю, и метод площадей становится не применимым. Также требуется, чтобы точка находилась в одной плоскости с треугольником, иначе метод площадей также не даст верного результата.
Как проверить, принадлежит ли точка треугольнику?
Для проверки принадлежности точки треугольнику можно использовать различные методы. Один из таких методов - это использование барицентрических координат. Сначала необходимо найти барицентрические координаты точки относительно вершин треугольника, а затем проверить, что все найденные координаты находятся в пределах от 0 до 1. Если это условие выполняется, то точка принадлежит треугольнику.



