Мы все знаем, что в математике существует множество задач и теорем, требующих от нас способности находить неизвестные делители множителей. Однако, иногда нам приходится столкнуться с ситуациями, когда мы не сможем прямо указать на эти делители с первого взгляда. Это может быть вызвано разными причинами, начиная от сложности численных вычислений, заканчивая наличием неизвестных переменных. Но не беда – сегодня мы расскажем вам о некоторых методах поиска неизвестных делителей фактора без использования привычных подходов.
В ходе нашего исследования, мы обнаружили несколько принципов и приемов, которые могут значительно облегчить поиск неизвестных делителей множителей. Во-первых, следует обратить внимание на окончания чисел или наличие общих численных элементов, которые могут указывать на возможные делители множителя. Например, если вы работаете с числами, заканчивающимися на 5, то, вероятно, имеется делитель 5. Это простой, но эффективный способ исключить лишние варианты и сосредоточиться на наиболее вероятных числах.
Еще одним полезным инструментом в нахождении неизвестных делителей является анализ простых чисел и их множителей. Простые числа имеют свойство быть делителями только самих себя и 1. Поэтому, если вы обнаружите простое число в качестве делителя, то у вас есть возможность упростить дальнейшие вычисления. Кроме того, анализируя множители простых чисел, вы можете раскрыть скрытые делители, которые могут быть скрыты в виде показательных функций или других сложных выражений.
Теория и алгоритмы для определения неведомого делителя умножителя числа
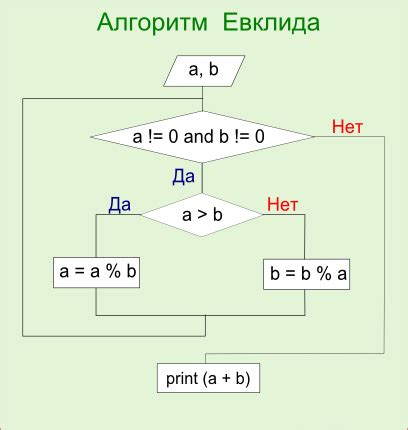
Этот раздел посвящен изучению и разработке алгоритмов для определения неизвестного фактора при умножении чисел. Мы будем исследовать различные подходы, методы и теоретические основы, которые помогут нам раскрыть значения неизвестных делителей, не обращаясь к конкретным определениям.
При анализе этой темы мы будем использовать методы, основанные на математических принципах и логике. Мы начнем с изучения простых чисел, их свойств и особенностей. Затем будут представлены различные алгоритмы, которые можно использовать для нахождения делителей чисел. Будут рассмотрены методы факторизации, такие как пробный делитель, метод Ферма и квадратичные вычеты.
Кроме того, мы рассмотрим некоторые концепции и теории, связанные с нахождением делителей, включая теорему о делителях и методы определения простоты чисел. Мы также изучим некоторые алгоритмы для эффективного нахождения делителей больших чисел, таких как алгоритм Кромера и методы, основанные на квадратичных вычетах.
В завершение, мы рассмотрим практические примеры и приложения, демонстрирующие применение различных алгоритмов для определения неизвестных делителей умножителей чисел. Тем самым, данные материалы предложат читателю полный обзор основных алгоритмов и теорий, которые помогут в нахождении значений неведомых делителей, наполнив его знаниями из области математики и криптографии.
Методы факторизации для определения неизвестного дивидента мультипликативного элемента

Перед нами предстоит исследование различных методов факторизации с целью нахождения незнакомого делителя множителя. Мы будем рассматривать способы разложения числа на простые множители и выбирать подходящий метод для определения неизвестного делителя, который поможет в решении задачи.
Для начала рассмотрим методы факторизации, основанные на представлении числа в виде произведения простых множителей. Один из таких методов – это метод полного перебора, при котором мы последовательно делим число на простые числа и проверяем, является ли результат деления целым числом. Если число делится без остатка, то мы нашли один из делителей множителя.
Другой метод – это метод пробного деления, основанный на поиске делителей до квадратного корня числа и проверке их делимости. Используя этот метод, мы можем найти все простые делители числа, а затем использовать их для определения неизвестного делителя.
- Метод квадратичного решета, основанный на поиске делителей, включает в себя поиск чисел, которые делятся на квадраты простых чисел плюс или минус 1. Эти числа могут быть потенциальными делителями множителя.
- Метод рационального квадратичного решета, основанный на поиске точных квадратных корней неприводимых квадратичных форм, также может быть использован для нахождения делителей множителя.
- Метод эллиптической кривой, использующий алгебраическую кривую, определенную над конечным полем, позволяет находить делители множителя.
В зависимости от специфики задачи и доступных средств, можно выбрать наиболее подходящий метод факторизации для нахождения неизвестного делителя множителя. Важно учитывать эффективность метода, его сложность и применимость к конкретному случаю. Работа с различными методами факторизации позволяет определить неизвестный делитель множителя и успешно решить поставленную задачу.
Алгоритмы решения простых и сложных случаев задачи определения фактора числа

Секреты отгадывания скрытой факторизации: проще, чем кажется!
Для того чтобы разделить число на простые множители, существуют разнообразные методы, которые позволят вам без труда раскрыть его тайны. Мы представим вам несколько надежных подходов, применимых как к простым, так и к сложным случаям. Закройте глаза на детали определений и множителей – и вы увидите, как просто и эффективно найти то, что вы ищете. Здесь мы вам расскажем про эти алгоритмы.
Универсальный полимер для разгадывания чисел – метод поиска общего знаменателя
Первый метод, который мы представим, позволяет найти общий делитель для любого числа, и даже углубиться в поиски нескольких множителей. Используя эту универсальную стратегию, вы обнаружите, что простые множители гармонично взаимодействуют друг с другом, образуя неизвестные делители, которые могут быть найдены с помощью упрощенных вычислений. Будьте внимательны к деталям и проявите искусство при раскрытии скрытых связей между числами.
Элегантный штрих для нахождения простых множителей – метод проб и ошибок
Второй метод, который мы рассмотрим, основан на использовании метода проб и ошибок. Это сложный, но элегантный подход, позволяющий вычислять простые делители числа путем систематического тестирования каждого возможного делителя. Подходящая комбинация терпения, логики и смекалки поможет вам обнаружить скрытые множители, заставив числа рассыпаться перед вами как паззл.
Таким образом, с помощью этих алгоритмов вы сможете эффективно разгадывать сложные проблемы, связанные с определением делителей множителей числа. Благодаря тщательному анализу и применению универсального полимера или метода проб и ошибок, вы сможете раскрыть скрытые связи чисел и отыскать скрытые множители, приближаясь к полной истине. Так давайте начнем разгадывать числа вместе!
Вопрос-ответ

Как определить неизвестный делитель множителя?
Для определения неизвестного делителя множителя нужно использовать метод простых делителей. Находим все простые числа, на которые делится множитель, а затем находим все возможные комбинации этих простых чисел, чтобы получить неизвестный делитель. Например, если множитель – 24 и известно, что он делится на простые числа 2 и 3, то возможные комбинации простых чисел – 2, 3, 2*3 = 6, 2*2 = 4, 2*2*3 = 12 и 2*2*3*3 = 72. Таким образом, возможные неизвестные делители множителя – 6, 4, 12 и 72.
Как использовать метод простых делителей для поиска неизвестного делителя множителя?
Для использования метода простых делителей для поиска неизвестного делителя множителя нужно знать, на какие простые числа делится множитель. Далее нужно составить все возможные комбинации этих простых чисел и записать их. Каждая комбинация будет являться потенциальным неизвестным делителем множителя. Например, если множитель – 30 и известно, что он делится на простые числа 2, 3 и 5, то список потенциальных неизвестных делителей будет состоять из 2, 3, 5, 2*3 = 6, 2*5 = 10, 3*5 = 15 и 2*3*5 = 30. Из этого списка можно выбрать и проверить каждое число для определения неизвестного делителя множителя.
Как выбрать неизвестный делитель множителя из списка потенциальных делителей?
Из списка потенциальных делителей можно выбрать неизвестный делитель множителя путем проверки каждого числа на делимость с множителем. Для проверки нужно поделить множитель на каждое из чисел списка. Если при делении получается целое число, то это число является делителем множителя. Например, если множитель – 24, а список потенциальных делителей – 6, 4, 12 и 72, то нужно проверить каждое число из списка. Заметим, что 24 делится на 6 – получается целое число. Значит, неизвестный делитель множителя равен 6.



