Алгебра – одна из самых увлекательных и практичных разделов математики, предлагающая нам постоянные головоломки и задачи для размышления и развития мышления. В этом разделе мы с вами решим одну из известных алгебраических задач, номер которой находится в 7-ом классе и составляет 589. Мы покажем, как легко и интересно можно решить данную задачу, используя базовые алгебраические навыки и логику.
Для того чтобы решить данную задачу, нам потребуются определенные знания и методы, которые помогут нам выявить подходящие стратегии и применить их. А дополнительно эта задача позволит нам развить наше алгебраическое мышление и логическое рассуждение. В процессе решения мы будем использовать различные алгебраические операции, смекалку и критическое мышление, а также представим необычные подходы к решению данной головоломки.
Давайте же вместе погрузимся в мир алгебры и начнем наше путешествие в решении интересной математической задачи! Вместе мы сможем разгадать все ее загадки и освоить важный навык, которым сможем успешно пользоваться как на уроках алгебры, так и в повседневной жизни.
Познакомьтесь с сутью условия задачи

В данном разделе предлагается рассмотреть основные аспекты и содержание условия задачи, представленной на уровне седьмого класса по алгебре.
Здесь мы проанализируем общую концепцию задачи и дадим краткую информацию о требуемых действиях и принципах, которые помогут успешно решить данную алгебраическую проблему.
Наши рекомендации не будут включать прямого решения задачи, а сместят акцент на важные моменты, с которыми следует познакомиться перед началом решения. В данном разделе вы найдете ключевые понятия, формулировки и способы подхода, которые помогут разобраться в общей сути задачи:
- Описание: Обозначение смысла задачи и постановка вопроса;
- Условия: Определение данных, предоставленных в задаче, и их значение в контексте решения;
- Требования: Изучение конкретных ожидаемых результатов, которые нужно получить в процессе решения задачи;
- Подход: Предложение основных идей и методов для решения задачи;
- Примеры: Демонстрация примеров и пошаговое объяснение применения предлагаемого подхода;
- Рекомендации: Предоставление советов и рекомендаций для успешного решения задачи;
Используя информацию, представленную в данном разделе, вы сможете лучше понять контекст и суть задачи, а также подготовиться к более наглядному и эффективному процессу ее решения.
Понимание основных понятий и терминов, применяемых в задаче

В данном разделе мы разберем ключевые понятия и термины, используемые в задаче. Понимание этих понятий и умение правильно интерпретировать термины играют важную роль в процессе решения задач по алгебре. Давайте рассмотрим их более подробно.
Вначале необходимо уяснить смысл каждого понятия, чтобы корректно использовать их в задаче. Например, если речь идет о переменной, то необходимо понять, что это неизвестное значение, которое может принимать различные значения в зависимости от контекста задачи.
Другим важным признаком является оператор, который определяет вид операции, выполняемой над переменными или числами в задаче. Например, знак "+", "-", "×" и "÷" обозначают сложение, вычитание, умножение и деление соответственно.
Также в задачах могут использоваться термины, такие как "уравнение", "неравенство" или "функция". Уравнение представляет собой математическое равенство, где два выражения сравниваются и приравниваются друг другу. Неравенство, в свою очередь, выражает отношение между двумя выражениями, где одно выражение больше или меньше другого. Функция - это математическое правило, определяющее соответствие между элементами двух множеств.
И последнее, но не менее важное понятие - "решение". Решение задачи в алгебре представляет собой нахождение значений переменных или выражений, удовлетворяющих условиям задачи и удовлетворяющих определенным правилам или ограничениям.
Анализ и разбор задачи на подзадачи

Статья предлагает подход к решению задачи алгебры 7 класса на основе анализа и разбора задачи на подзадачи. Методика заключается в разделении сложной задачи на более простые и понятные задачи, что облегчает ее решение и позволяет получить полное и корректное решение.
Прежде чем приступить к решению задачи алгебры 7 класса, необходимо проанализировать ее и определить, какие подзадачи она включает. Отделение сложных задач на более простые и понятные помогает структурировать процесс решения и сделать его более эффективным.
В ходе анализа задачи следует выделить основные элементы, такие как известные данные, неизвестные значения, условия и ограничения. Затем каждая подзадача должна быть рассмотрена отдельно с использованием соответствующих алгебраических методов и формул.
Пример:
Рассмотрим задачу, связанную с вычислением площади прямоугольника. Известно, что одна из сторон прямоугольника равна 5 см, а отношение длины другой стороны к первой стороне равно 3/4. Требуется найти площадь прямоугольника.
В данном случае, основные подзадачи могут быть определены как: нахождение второй стороны прямоугольника и вычисление площади. Сначала необходимо использовать заданные данные и соотношение длин сторон, чтобы найти вторую сторону прямоугольника. Затем, используя полученные значения, можно вычислить площадь прямоугольника.
Анализ и разбор задачи на подзадачи при решении задач алгебры 7 класса позволяет более системно и логично подойти к решению. Этот метод позволяет избежать путаницы и ошибок, а также получить полное и корректное решение задачи.
Применение известных алгоритмов и методов в решении алгебраических задач

В данном разделе будет рассмотрено использование уже известных алгоритмов и методов, которые помогут вам решить задачу алгебры 7 класса номер 589. Мы рассмотрим различные подходы и техники, которые позволят эффективно и грамотно решить эту задачу.
Одним из таких подходов является использование алгоритма "перебора". Этот метод позволяет производить последовательное перебор всех возможных вариантов решения задачи и выбрать наилучший из них. Применение этого алгоритма может быть особенно полезным в случаях, когда у вас есть конкретные условия, которые необходимо учесть.
Кроме того, мы рассмотрим метод "анализа и синтеза". Этот подход предполагает разбиение задачи на отдельные компоненты, исследование каждого компонента в отдельности, а затем синтезирование полученных решений для получения окончательного результата. Применение этого метода позволит вам лучше понять каждую часть задачи и найти оптимальное решение.
Дополнительно, мы рассмотрим использование таблиц и графиков для визуализации данных и упрощения алгебраических вычислений. Таблицы позволяют упорядочить информацию и легко сравнивать различные варианты, а графики помогут наглядно представить связи и зависимости между переменными и значениями в задаче.
| Применяемые алгоритмы и методы: |
|---|
| Алгоритм "перебора" |
| Метод "анализа и синтеза" |
| Использование таблиц и графиков |
Построение математической модели для решения задачи

В данном разделе мы рассмотрим процесс построения математической модели, которая позволит нам решить задачу алгебры 7 класса номер 589. Для проведения анализа и нахождения решения мы будем использовать различные математические инструменты и концепции, которые помогут нам формализовать представленную задачу.
Первым шагом в построении модели является определение входных данных и конечной цели задачи. Далее, мы приступаем к выделению ключевых переменных и параметров, которые будут участвовать в решении. Необходимо обратить внимание на смысл каждого из этих элементов и их взаимосвязь друг с другом.
Затем мы переходим к формализации задачи путем создания уравнений, неравенств или систем уравнений, которые будут описывать связи между переменными и параметрами. Важно правильно выбрать эти уравнения, учитывая условия задачи, чтобы раскрыть всю необходимую информацию и найти искомый результат.
После построения математической модели мы приступаем к решению полученных уравнений или систем уравнений. Для этого мы применяем методы и алгоритмы, соответствующие данной задаче и используем доступные математические инструменты, такие как алгебраические операции, факторизация, подстановка значений и др. С помощью этих методов мы получаем искомый результат и проверяем его на соответствие поставленной задаче.
Таким образом, построение математической модели является важным этапом решения задачи алгебры. Оно позволяет нам абстрагироваться от конкретной формулировки задачи и работать с абстрактными математическими объектами, которые помогают нам лучше понять суть и решить задачу.
Вычисление значений и промежуточных результатов при решении алгебраической задачи

Один из ключевых аспектов при решении задач алгебры - это вычисление промежуточных результатов, которые позволяют логическишаг за шагом приближаться к окончательному решению. Например, в задачах с использованием уравнений, мы вычисляем значения переменных и заменяем их в уравнении, чтобы найти промежуточное решение, которое затем используется в дальнейших вычислениях.
Вычисление значений и промежуточных результатов также позволяет проводить проверку правильности полученного решения. Путем замены найденных значений обратно в задачу и выполнения несложных вычислений, мы можем убедиться, что полученное решение удовлетворяет условию задачи.
Итак, важность вычисления значений и промежуточных результатов в задачах алгебры не может быть переоценена. Тщательное проведение этих вычислений помогает нам последовательно продвигаться в решении задачи, логически связывать различные шаги и убедиться в правильности окончательного решения.
Проверка правильности решения и анализ полученного ответа
В данном разделе мы проведем проверку решения задачи алгебры седьмого класса и проанализируем полученный ответ с целью убедиться в его правильности и полноте.
Подтверждение правильности решения
В первую очередь, мы осуществим проверку выполнения всех необходимых шагов решения задачи. Для этого взглянем на использованные формулы, операции и промежуточные результаты, чтобы убедиться, что все они были применены корректно и последовательно. Также важно проверить, были ли учтены все заданные условия и данные задачи при выполнении решения.
Анализ полученного ответа
После проверки правильности решения переходим к анализу полученного ответа. В этом этапе следует обратить внимание на нужность и достаточность полученных результатов для решения поставленной задачи. Можно оценить ответ на основе его соответствия заданному вопросу и его содержательности. Также важно проверить, правильно ли были интерпретированы числовые значения в рамках решения задачи и соответствуют ли они действительности.
Корректировка решения и ответа
Если при проверке решения были замечены ошибки или если полученный ответ не удовлетворяет требованиям задачи, необходимо внести корректировки. На этом этапе можно пересмотреть примененные формулы и операции, проверить правильность использования данных и условий задачи, а также исправить ошибки в вычислениях. В результате корректировок мы получим окончательное правильное решение и адекватный ответ на задачу.
Финальная проверка
После внесения корректировок следует провести финальную проверку решения и полученного ответа. На этом этапе убедимся, что все ошибки исправлены, соответствуют требованиям задачи и решение выполнено полностью и правильно.
Представление ответа в виде логической и четкой записи
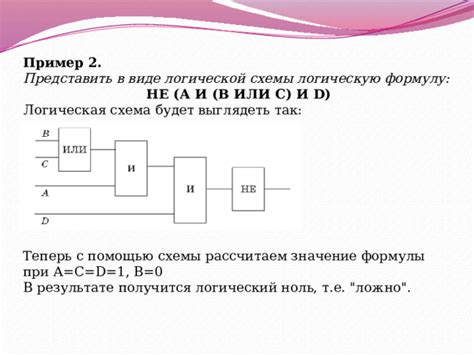
Когда мы получаем ответ на поставленную алгебраическую задачу, важно уметь описать его с помощью логических выражений, математических символов и языка алгебры. Для этого необходимо использовать точные и ясные определения, которые помогут читателю или слушателю нашего ответа понять представленную информацию.
При представлении ответа в виде стройной записи стоит обратить внимание на наличие ключевых слов, связывающих условие задачи с искомым результатом. Такие слова, как "сумма", "разность", "количество" и другие, помогают описать ответ на языке математики, тем самым упрощая понимание решения.
Важно также правильно оформить ответ с использованием математических символов. Например, для представления формул и уравнений можно использовать функциональные символы (+, -, ×, ÷, =, ≤, ≥) и математические операторы (sin, cos, tan, ln и др.). Это поможет создать более четкую и компактную запись решения задачи.
Кроме того, следует обратить внимание на использование переменных и их объявление. В случае, когда нужно найти несколько искомых величин, для каждой из них обычно используют разные буквы или символы, чтобы избежать путаницы при чтении ответа. Определение переменных четко определяет, какая именно величина имеется в виду в каждом конкретном случае.
Итак, представление ответа в виде стройной и понятной записи играет важную роль в успешном решении алгебраических задач. Четкое использование логических выражений, математических символов, ключевых слов и верное объявление переменных сделает ваш ответ более понятным и легко читаемым для других.
Альтернативные подходы к решению задачи

В данном разделе рассмотрим различные методы и подходы, которые могут быть использованы для решения данной алгебраической задачи класса 7, номер 589, без применения стандартного алгоритма.
1. Вариация изначальных условий
Один из подходов к решению задачи заключается в изменении изначальных условий, что может привести к упрощению решения. Размышляйте о том, какие переменные можно изменить или как можно переформулировать задачу, чтобы найти более эффективный способ ее решения.
2. Применение графического представления
Второй способ состоит в использовании графического представления задачи. Иногда построение графика или диаграммы может помочь наглядно представить условия задачи и обнаружить более простой или элегантный путь к ее решению.
3. Использование аналогий и анализ аналогичных задач
Третий подход заключается в поиске аналогий и анализе решений аналогичных задач. Зачастую, решение задачи может быть обнаружено через поиск связей с другими известными проблемами или путем анализа методов и подходов, которые успешно применялись в других задачах.
4. Использование символьных или численных методов
Кроме того, можно использовать символьные или численные методы для решения задачи. Некоторые задачи легче решать с использованием математической символики, формул или систем уравнений, тогда как другие могут быть решены только с применением численных методов или выполнением вычислений.
Учитывая вышеуказанные альтернативные методы и подходы, важно экспериментировать и искать новые пути решения задачи. Не стесняйтесь пробовать различные подходы и анализировать их эффективность, чтобы найти наиболее подходящее решение задачи алгебры 7 класса номер 589.
Вопрос-ответ

Как решить задачу алгебры 7 класса номер 589?
Для решения задачи алгебры 7 класса номер 589, вам следует внимательно прочитать условие задачи и уяснить, что вам требуется найти или решить. Затем следует анализировать данную информацию и использовать соответствующие алгебраические методы и формулы для решения задачи. Возможно, вам потребуется использовать знания о пропорциях, уравнениях, системах уравнений и т.д. Если вы столкнулись с трудностями при решении данной задачи, рекомендуется обратиться к учебнику или попросить помощи учителя.
Какие знания алгебры необходимы для решения задачи 7 класса номер 589?
Для решения задачи алгебры 7 класса номер 589, вам потребуются знания о пропорциях, уравнениях и системах уравнений. Возможно, придется использовать такие понятия, как коэффициенты, переменные, операции с алгебраическими выражениями и т.д. Более конкретные знания, необходимые для решения задачи, могут быть указаны в условии самой задачи или предшествующие этой задаче материалы из учебника.
Можете ли вы привести пример задачи алгебры 7 класса с решением?
К сожалению, без конкретного условия задачи алгебры 7 класса, невозможно дать полноценное решение. Однако, я могу привести пример задачи и по шагам показать, как ее решить. Например, предположим, что у нас есть задача о поиске неизвестного числа. В таком случае, мы можем сформулировать уравнение, используя информацию, предоставленную в условии задачи, и затем решить это уравнение, чтобы найти неизвестное число. Чтобы решить конкретную задачу, рекомендую обратиться к учебнику или учителю для получения дополнительной помощи.
Как решить задачу алгебры 7 класса номер 589, если не знаю, какой метод применить?
Если вы не знаете, какой метод применить, вам следует внимательно прочитать условие задачи и выделить все известные и неизвестные величины. После этого, можно попробовать подобрать подходящий метод решения, исходя из типа задачи и данной информации. Если у вас все равно возникают сомнения, лучше обратиться за помощью к учителю или одноклассникам, которые могут поделиться своими идеями и подсказками.
Какую формулу использовать для решения задачи алгебры 7 класса номер 589?
Для того, чтобы определить какую формулу использовать для решения задачи, вам нужно внимательно прочитать условие и выделить все известные величины. Затем, проанализировав информацию, можно попытаться определить, какие математические связи между величинами могут быть использованы в задаче. Если у вас возникают затруднения, вы можете обратиться за помощью к учителю или одноклассникам, которые могут подсказать подходящую формулу для решения конкретной задачи.
Как проверить правильность решения задачи алгебры 7 класса номер 589?
Для проверки правильности решения задачи алгебры 7 класса номер 589, вы можете выполнить следующие шаги. Во-первых, просмотрите ваше решение и убедитесь, что вы правильно применили все математические операции и формулы. После этого, внимательно перечитайте условие задачи и проверьте, что все известные величины были правильно использованы. Наконец, выполните несколько арифметических операций, чтобы проверить, что ваше решение соответствует условию задачи и даёт корректный результат. Если у вас остаются сомнения, всегда полезно обратиться к учителю или одноклассникам для проверки их мнения о вашем решении.



