В мире науки и техники существует множество проблем, для решения которых требуется знание геометрии. Одной из таких проблем является нахождение площади сечения. Это важная задача, на которую могут наткнуться специалисты различных областей, начиная от инженеров и заканчивая архитекторами и физиками.
Понятие "сечение" означает пересечение плоскости с объемным телом. Такое пересечение может иметь самые разнообразные формы - от плоских круговых сечений до сложных многоугольных. При расчете площади сечения, требуется определить точные значения площади, чтобы учесть различные физические и инженерные законы и принципы.
В настоящее время существует несколько методов и формул для расчета площади сечения. Одним из наиболее распространенных методов является использование теоремы Пифагора и базовых формул геометрии. Этот метод основан на определении геометрических особенностей заданного сечения и подсчете соответствующих размеров и углов.
Основные термины и определения

В данном разделе мы рассмотрим основные понятия, которые необходимо знать для понимания методов нахождения площади сечения.
- Сечение – это плоская фигура, получаемая пересечением тела или поверхности с плоскостью. Оно может быть различных форм и размеров.
- Площадь сечения – это величина, показывающая, сколько пространства занимает данное сечение. Она измеряется в квадратных единицах.
- Методы нахождения площади сечения – существует несколько способов определения площади сечения в зависимости от его формы и характеристик. В данной статье мы рассмотрим основные методы и формулы, которые помогут нам решить эту задачу.
- Формула – это математическое выражение, которое позволяет вычислить значение определенной величины. В случае с площадью сечения, формулы позволяют нам получить соответствующий результат и использовать его для дальнейших вычислений.
- Синонимы – это слова, имеющие сходное значение, но различающиеся по форме или оттенку. В данной статье мы постараемся разнообразить текст, используя более разнообразные выражения и термины.
Теперь, когда мы ознакомились с основными понятиями и определениями, перейдем к рассмотрению методов и формул, которые помогут нам найти площадь сечения.
Использование метода прямоугольной сетки для определения площади сечения

В данном разделе будет рассмотрен метод, основанный на использовании прямоугольной сетки для определения площади сечения. Этот метод позволяет приближенно вычислить площадь сечения объекта, используя набор прямоугольных областей, которые покрывают данное сечение. Используя эту сетку, возможно определить площади каждой из частей сечения и сложить их, получив приближенное значение площади сечения.
| Шаг 1 | Шаг 2 | Шаг 3 | Шаг 4 |
|---|---|---|---|
| Разбитие сечения на прямоугольники | Определение площади каждого прямоугольника | Суммирование площадей прямоугольников | Получение приближенного значения площади сечения |
| Для начала необходимо разделить сечение объекта на ряд прямоугольных областей, используя прямоугольную сетку. Это можно сделать путем задания интервалов для координаты x и y и создания прямоугольников, охватывающих данные интервалы. | Каждому из созданных прямоугольников следует определить его площадь, используя соответствующую формулу для площади прямоугольника. Для этого необходимо знать значения длины и ширины каждого прямоугольника. | После определения площадей всех прямоугольников, их значения следует просуммировать. Полученная сумма будет приближенным значением площади сечения объекта. | Таким образом, используя метод прямоугольной сетки, можно приближенно определить площадь сечения объекта, разбив его на прямоугольные части и вычислив площадь каждой из них. Этот метод дает достаточно точные результаты при правильном выборе размера прямоугольных областей. |
Использование метода интегралов для определения площади сечения

Определенный интеграл - это математический инструмент, который позволяет вычислить площадь под кривой на определенном интервале. При использовании метода интегралов для нахождения площади сечения, нужно разбить кривую на бесконечное количество малых элементов и приблизить площадь каждого элемента с помощью интеграла.
Для вычисления площади сечения с использованием метода интегралов, необходимо знать уравнение кривой или границы сечения, а также пределы интегрирования, которые определяют интервал на оси, вдоль которой происходит интегрирование. После разбиения кривой на малые элементы и вычисления площади каждого элемента, полученные значения можно сложить, чтобы получить общую площадь сечения.
Метод интегралов для определения площади сечения может быть применен к различным типам сечений, включая простые геометрические фигуры, такие как треугольники и прямоугольники, а также более сложные кривые и поверхности. Этот метод является эффективным инструментом для вычисления площади сечения и позволяет получить точные результаты в широком диапазоне задач и приложений.
Использование графических методов при рассмотрении сечения
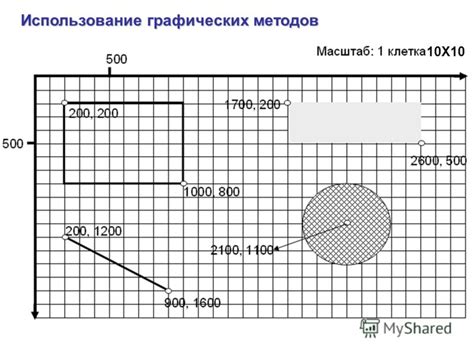
В данном разделе рассмотрим возможность использования графических методов для определения площади сечения. Графические методы представляют собой визуальные подходы, позволяющие наглядно представить форму сечения и вычислить его площадь без применения конкретных математических формул.
Одним из графических методов, широко используемым при анализе сечений, является метод графического интегрирования. Он основывается на принципе разбиения сечения на малые элементы и последующей аппроксимации их формы. Далее, на основе этих данных, можно рассчитать площадь сечения с помощью соответствующих графических вычислений.
Вторым графическим методом, который может быть использован при анализе сечений, является метод графического вычисления площади через измерение. Он заключается в создании масштабной модели сечения и последующем измерении площади с помощью известных инструментов, таких как линейка или калькулятор. Такой метод позволяет определить площадь сечения даже при отсутствии точных математических формул или сложных вычислений.
Использование графических методов в расчетах сечения представляет собой эффективный и наглядный способ определить площадь сечения без необходимости применения строго формализованных математических формул и методов. Они позволяют получить результаты приближенного характера, которые могут быть использованы для общего анализа и практических расчетов.
| Преимущества | Недостатки |
|---|---|
| Простота использования | Приближенный характер результатов |
| Наглядность и интуитивность | Зависимость точности от масштаба изображения |
| Возможность обхода сложных математических формул | Ограниченные возможности для сложных сечений |
Способы определения площади сечения сложных форм
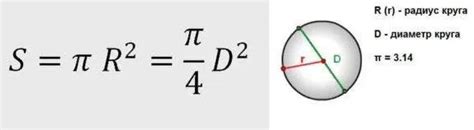
Многообразие фигур обусловлено разнообразием предметов и объектов, которые оказываются подвергнутыми измерению площади своих сечений. Как правило, сечения таких форм отличаются от простых геометрических фигур, представляя собой более сложные и запутанные образования. В связи с этим, необходимо уметь определить площадь сечений сложных форм, используя различные способы и подходы.
Первый способ состоит в аппроксимации сложной формы сечения простыми геометрическими фигурами, такими как прямоугольники, круги или треугольники. После этого можно вычислить площадь каждой из этих фигур и суммировать их результаты для получения приближенного значения площади сечения в целом.
Второй способ заключается в использовании метода интегрирования. Он подразумевает разделение сложной формы сечения на бесконечно малые элементы, для которых можно найти элементарную площадь. Затем эти элементарные площади складываются интегрированием, что позволяет получить точное значение площади сечения без использования аппроксимации.
Третий способ основан на применении математических моделей и компьютерного моделирования для определения площади сечения сложной формы. Пользуясь методами численного анализа и компьютерными алгоритмами, можно построить точную математическую модель сложной фигуры и вычислить её площадь с высокой степенью точности.
Каждый из этих способов имеет свои особенности и применяется в зависимости от конкретной задачи и требуемой точности. Изучение и применение данных способов позволяет эффективно находить площадь сечений сложных форм и применять их в различных областях науки, техники и промышленности.
Формула площади круглого сечения и ее применение

Формула площади круглого сечения основана на известной математической константе - числе π (пи). Она позволяет вычислить площадь поверхности, ограниченной окружностью, которая образует сечение объекта или материала.
Для применения формулы необходимо знать радиус окружности, которая образует круглое сечение. Радиус - это расстояние от центра окружности до ее края. Подставив значение радиуса в формулу, мы можем вычислить площадь такого сечения.
Применение формулы площади круглого сечения имеет широкий спектр. Например, в строительстве она позволяет расчитать площадь колонн, столбов или опор, имеющих круглое сечение. В машиностроении она применяется для определения площади поперечного сечения валов, труб и других деталей, где форма имеет круглую или близкую к ней геометрию.
Кроме того, формула площади круглого сечения является основой для других расчетов, связанных с этим типом сечения. Например, она может использоваться для определения объема материала, необходимого для создания объекта или конструкции, или для расчета площади поверхности, необходимой для нанесения покрытия или отделки.
Особенности расчета площади сечения полигональных объектов

В данном разделе мы рассмотрим особенности и специфику вычисления площади сечения полигональных объектов. Проанализируем уникальные методы и формулы, позволяющие определить площадь поверхности, ограниченной полигоном, при сохранении грамотности и точности расчетов.
- Закономерности исчисления площади: Вместо использования общепринятых алгоритмов, привычных для геометрических фигур, расчет площади полигональных объектов требует специального подхода. Необходимо учитывать особые свойства отрезков и углов, составляющих полигон.
- Индивидуальные особенности: Каждый полигон имеет уникальные характеристики. Это могут быть неровные стороны, сложные углы, наличие полилиний, разнообразные вариации пересечений сторон. Расчет площади сечения требует учета всех этих особенностей для получения точного результата.
- Специализированные формулы: Научное сообщество разработало специальные формулы и методы для расчета площади полигональных объектов. Некоторые из них основаны на принципе разбиения полигона на треугольники и вычисления площадей каждой из частей. Другие формулы учитывают размеры сторон и углы между ними.
- Использование программных инструментов: Для более эффективных вычислений площади сечения полигональных объектов можно воспользоваться специализированными программными инструментами и алгоритмами, которые автоматически обрабатывают данные и предоставляют точный результат.
В итоге, понимание особенностей расчета площади сечения полигональных объектов является необходимым для точной и грамотной работы с такими геометрическими формами. Знание уникальных методов и формул позволяет получать правильные результаты и применять их в различных областях, где требуется изучение и анализ полигональных объектов.
Расчет площади сечения трапеции и трапецеиды
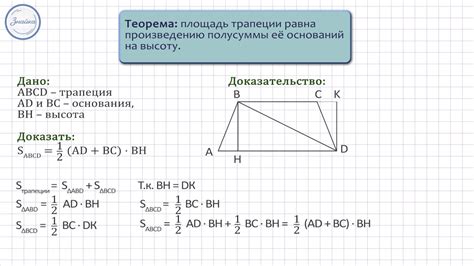
Начнем с определения. Трапеция - это четырехугольник, у которого две стороны параллельны, а две другие стороны не параллельны. Трапецеида является обобщением трапеции, у которой все четыре стороны могут быть непараллельны.
Для расчета площади сечения трапеции необходимо знать длины оснований (большего и меньшего) и высоту (расстояние между основаниями). Площадь трапеции можно вычислить по формуле, которая основана на умножении средней линии на высоту.
При расчете площади сечения трапецеиды мы должны знать длины оснований (верхнего и нижнего), высоту (расстояние между основаниями) и наклон боковых ребер. Формула для расчета площади трапецеиды включает вычисление средней линии и умножение ее на высоту.
Используя описанные формулы, можно легко и точно определить площадь сечения трапеции и трапецеиды, что является важным этапом во многих инженерных и строительных проектах.
Примеры вычисления площади сечения разнообразных геометрических фигур
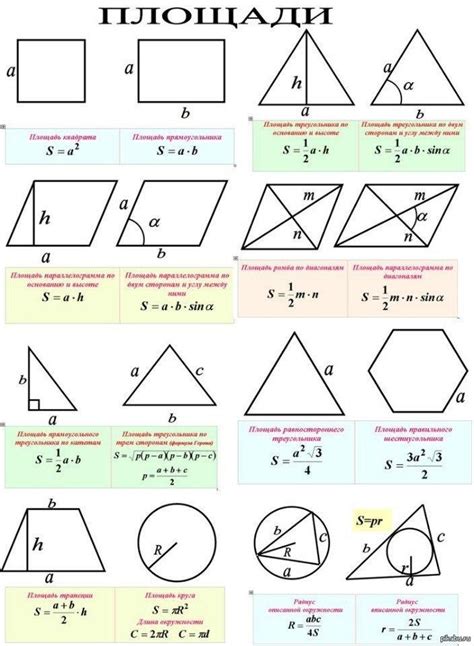
В данном разделе рассмотрим примеры расчёта площади сечения различных геометрических фигур. Вычисление площади сечения одна из важных задач в различных областях, таких как инженерия, архитектура и геометрия. Вам предоставятся подробные примеры решения, которые помогут вам разобраться в процессе вычисления площади таких фигур, как круг, треугольник, прямоугольник, трапеция и многое другое.
| Геометрическая фигура | Пример вычисления площади сечения |
|---|---|
| Круг | Определение радиуса круга и использование формулы для вычисления площади сечения круга. |
| Треугольник | Использование формулы Герона для вычисления площади сечения треугольника по известным сторонам. |
| Прямоугольник | Применение формулы для вычисления площади сечения прямоугольника, используя известные стороны. |
| Трапеция | Определение длин оснований и высоты трапеции, а затем использование формулы для расчета площади сечения. |
Эти примеры помогут вам освоить различные методы вычисления площади сечения разных геометрических фигур. Следуя подробному решению каждого примера, вы сможете точно определить площадь фигуры и применить эти знания на практике.
Вопрос-ответ

Как найти площадь сечения методом прямоугольника?
Чтобы найти площадь сечения методом прямоугольника, необходимо знать длину и ширину сечения. Площадь сечения рассчитывается по формуле: S = a * b, где a - длина сечения, b - ширина сечения.
Как найти площадь сечения методом круга?
Для расчета площади сечения круга необходимо знать радиус сечения. Формула расчета площади сечения круга выглядит следующим образом: S = π * r^2, где π - математическая константа, близкая к 3,14, r - радиус сечения.
Как найти площадь сечения методом треугольника?
Расчет площади сечения методом треугольника требует знания длин двух сторон треугольника и угла между ними. Формула расчета площади сечения треугольника выглядит следующим образом: S = (a * b * sin(γ))/2, где a и b - длины сторон треугольника, γ - угол между этими сторонами (измеряется в радианах).
Как найти площадь сечения методом эллипса?
Площадь сечения эллипса рассчитывается по формуле: S = π * a * b, где a и b - полуоси эллипса. Необходимо знать значения полуосей для расчета площади.
Можно ли найти площадь сечения нестандартной фигуры?
Да, можно найти площадь сечения нестандартной фигуры. Для этого нужно разбить эту фигуру на более простые геометрические фигуры, для которых известны формулы расчета площади, например, прямоугольники, треугольники или круги. Затем нужно вычислить площади каждой из этих фигур и сложить их.



