В мире математики существует увлекательная область, в которой функции оживают и приобретают новую размерность. Речь идет о построении касательной к графику функции - незыблемом инструменте, позволяющем нам погрузиться в увлекательный мир кривых.
Касательная, как невидимый проводник, открывает перед нами возможности для определения скорости изменения функции в каждой ее точке, позволяет найти ее точку перегиба и сделать предположения о поведении графика в целом. Она выступает в роли виртуозного спринтера, покоряющего мгновенные изменения функции и отражающего их в точке касания.
Чтобы окунуться в эту увлекательную тему, необходимо разобраться с основами достижения согласованности между графиком функции и его касательной. Зная секреты дифференцирования, мы получим возможность приблизиться к грациозному замыслу функции и тщательно исследовать ее движение на всем протяжении области определения.
Предлагаем вам отправиться в увлекательное путешествие в мир касательных, где каждый шаг будет приближать нас к грандиозным открытиям и новым гармоничным взаимодействиям функций и графиков. Будьте готовы выйти за рамки обыденного и открыть для себя тайны особых точек и сглаженности, даруемой касательной.
Основные принципы построения касательной линии к кривой
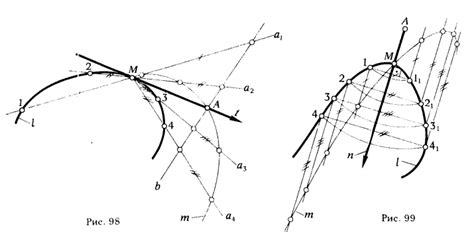
В этом разделе мы изучим основные принципы, которые лежат в основе построения касательной кривой к графику функции. Мы рассмотрим методы определения точки касания, угла наклона и уравнения самой линии, используя различные подходы и техники.
Определение точки касания
Прежде чем строить касательную линию, необходимо определить точку, где линия касается графика функции. Для этого мы используем метод дифференцирования функции в данной точке. Дифференциал функции показывает скорость изменения в данной точке и является ключевым элементом в определении точки касания.
Угол наклона касательной
Касательная линия имеет свойство именно касаться графика функции в определенной точке, и ее угол наклона определяет скорость изменения функции в этой точке. Мы рассмотрим различные методы расчета угла наклона, включая использование производной функции и геометрические подходы.
Уравнение касательной линии
Одним из центральных вопросов при построении касательной линии является нахождение ее уравнения. Мы рассмотрим различные подходы к определению уравнения, включая использование производной функции, формулы точки-наклона и тангенса угла наклона.
Понимание основных принципов построения касательной кривой к графику функции позволит нам более глубоко изучить поведение функций и улучшить наши навыки анализа графиков.
Определение касательной и его свойства
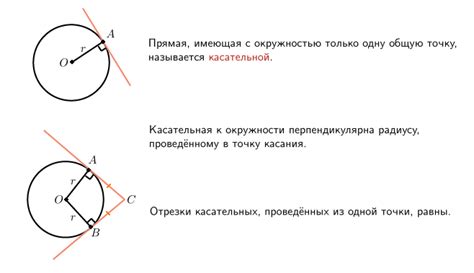
Первое свойство, которое следует отметить, это то, что касательная всегда касается графика функции в одной точке. Это означает, что у прямой и графика функции есть общая точка касания, которая называется точкой касания. В этой точке значения координаты "x" и "y" для графика функции и касательной совпадают.
Второе свойство заключается в том, что касательная имеет общий наклон с графиком функции в точке касания. Это означает, что если наклон графика функции увеличивается, то и наклон касательной также увеличивается, и наоборот. Кроме того, если график функции является вогнутым, то касательная будет находиться ниже графика функции в точке касания, а если график функции выпуклый, то касательная будет находиться выше графика функции.
Третье свойство связано с производной функции. Касательная к графику функции может быть представлена в виде линии, заданной уравнением, в котором используется производная функции и координаты точки касания. Производная функции в точке касания определяет наклон касательной. Если производная функции положительна в точке касания, то касательная имеет положительный наклон, и наоборот.
Изучение и понимание понятия касательной и его свойств позволяет анализировать поведение функций и находить важные точки на графиках функций. Касательные являются полезным инструментом в решении задач, связанных с определением экстремумов функций, анализом скорости изменения функций и различных траекторий движения.
Шаги построения касательной к кривой функции
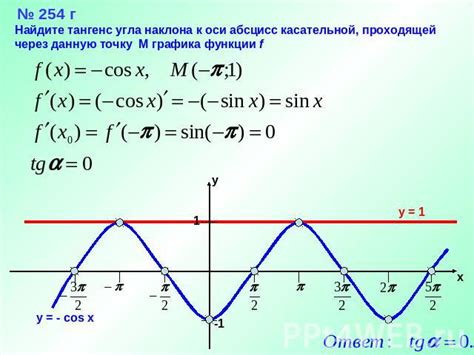
В этом разделе будет рассмотрено пошаговое руководство по построению касательной к графику функции. Для этого мы будем использовать различные методы и инструменты, которые позволят нам определить точку касания и наклон касательной линии.
- Выберите точку на графике функции, в которой вы хотите построить касательную. Эта точка должна быть достаточно близкой к точке, в которой вы хотите найти касательную.
- Определите значение функции в выбранной точке. Для этого подставьте координаты данной точки в уравнение функции.
- Найдите производную функции с помощью соответствующей формулы или метода дифференцирования. Она позволит определить наклон касательной в выбранной точке.
- Подставьте найденное значение наклона и координаты выбранной точки в уравнение касательной линии. Это уравнение имеет вид y = mx + b, где m - наклон касательной, x и y - координаты выбранной точки, b - свободный член.
- Используйте полученное уравнение для построения касательной в рамках выбранного интервала.
Теперь вы знаете основные шаги построения касательной к графику функции. Следуя этому руководству, вы сможете найти точку касания и построить касательную линию, что поможет в изучении поведения функции в данной точке.
Методы определения уравнения касательной

В данном разделе мы рассмотрим некоторые способы нахождения уравнения касательной к графику функции без применения сложных математических определений. Благодаря этим методам вы сможете эффективно определить уравнение касательной и использовать его для решения различных практических задач.
1. Геометрический метод
Первым методом является геометрический подход, основанный на наблюдениях и связях между графиком функции и касательной. При использовании этого метода вы можете определить точку касания графика функции и касательной, а также угол наклона касательной. Затем, используя эти данные, можно определить уравнение касательной в виде y = kx + b, где k - коэффициент наклона, а b - точка пересечения с осью ординат.
2. Тангенсальная линия
Второй метод основан на представлении касательной в виде тангенсальной линии, которая касается графика функции в одной точке и имеет тот же угол наклона. Для определения уравнения касательной этим методом необходимо найти производную функции в данной точке и затем использовать ее значение для составления уравнения касательной.
3. Линейная аппроксимация
Третий метод, называемый линейной аппроксимацией, заключается в приближенном представлении функции линейной функцией. Для этого необходимо выбрать две близкие точки на графике функции и использовать их координаты для определения параметров уравнения касательной в виде y = kx + b. Чем ближе выбранные точки к искомой, тем точнее будет полученное уравнение касательной.
Таким образом, выбирая подходящий метод нахождения уравнения касательной, вы сможете применять его для практического решения задач, связанных с графиками функций и их анализом.
Примеры применения касательной в реальных задачах
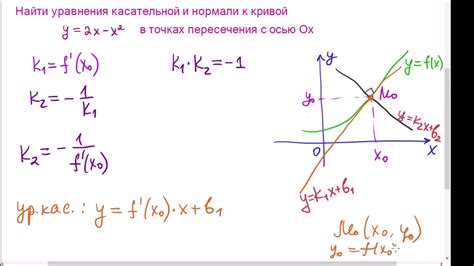
Давайте рассмотрим несколько практических ситуаций, где понимание и применение касательной к графику функции может быть полезным инструментом.
- Минимизация ошибок в конструкции. Построение касательной к графику функции позволяет оценить поведение функции вблизи определенной точки и найти ее наилучшую аппроксимацию. Таким образом, можно оптимизировать процесс проектирования и избежать возможных ошибок.
- Определение скорости изменения. Касательная к графику функции представляет собой линию, которая наилучшим образом аппроксимирует функцию в заданной точке. Используя эту линию, можно определить скорость изменения функции в данной точке, что может быть полезным в различных областях, например, в физике или экономике.
- Решение оптимизационных задач. При решении оптимизационных задач часто требуется найти точку максимума или минимума функции. Рассмотрение касательной к графику функции в окрестности этих точек помогает локализовать их и разработать соответствующие практические решения.
- Анализ поведения процессов. В некоторых процессах можно использовать касательную к графику функции для анализа и прогнозирования поведения этих процессов. Например, в экономике касательная к функции спроса может использоваться для предсказания изменений спроса в зависимости от различных факторов.
Приведенные примеры демонстрируют только некоторые из возможных применений касательной к графику функции в практических задачах. Понимание этого концепта может быть полезным инструментом при решении различных задач и анализе различных процессов в различных областях знаний.
Вопрос-ответ

Как построить касательную к графику функции?
Для построения касательной к графику функции необходимо определить точку, через которую должна проходить касательная, и ее угловой коэффициент. Угловой коэффициент можно найти, вычислив производную функции в данной точке. Затем, используя найденную точку и угловой коэффициент, можно построить уравнение прямой, являющейся касательной к графику функции, и провести соответствующую прямую на графике.
Как найти точку, через которую должна проходить касательная?
Для нахождения точки, через которую должна проходить касательная, необходимо выбрать определенную точку на графике функции. Эта точка должна быть близкой к месту, где требуется построить касательную. Часто в качестве такой точки выбирают точку с известными координатами, чтобы упростить расчеты.
Как найти угловой коэффициент касательной?
Угловой коэффициент касательной можно найти, вычислив производную функции в заданной точке. Для этого необходимо записать уравнение производной функции и подставить в него координаты точки, через которую должна проходить касательная. Полученное значение будет являться угловым коэффициентом касательной.
Как построить уравнение прямой касательной?
Чтобы построить уравнение прямой, являющейся касательной к графику функции, нужно использовать найденную точку и угловой коэффициент. Уравнение прямой может быть записано в виде y = mx + c, где m - угловой коэффициент, x и y - координаты точки, а c - свободный член. Подставляя значения коэффициента и координат точки в уравнение, можно найти значение свободного члена и окончательно записать уравнение касательной.
Как провести касательную на графике функции?
Проведение касательной на графике функции после построения уравнения прямой осуществляется с помощью трассировки. Для этого нужно определить несколько точек на прямой касательной и соединить их линией. Затем, используя эти точки, провести линию на графике. Касательная будет представлена в виде прямой, проходящей через выбранные точки и приближенно повторяющей форму графика функции в данной области.



