Понимание углов и их значения является неотъемлемой частью геометрии и математики в целом. Углы - это не только понятие, необходимое для работы с геометрическими фигурами, но и основа для многих других математических разделов. Особое внимание уделяется углам и их свойствам, в том числе их мерам, которые измеряются с помощью тригонометрических функций.
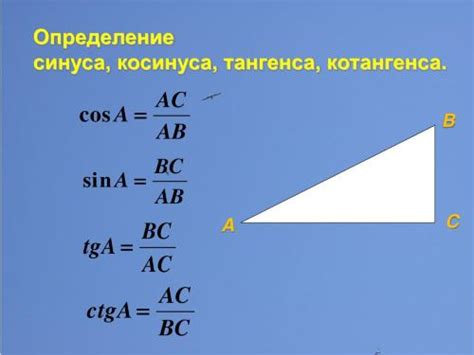
Одной из таких функций является косинус, который определяется как отношение длины прилежащего катета к гипотенузе прямоугольного треугольника. Косинус угла играет очень важную роль в различных областях, включая физику, инженерию и компьютерную графику.
Но как найти значение косинуса угла? Существует несколько простых способов расчета. Они основаны на применении различных формул и трюков, которые помогут нам определить точное значение косинуса для заданного угла. Такой подход позволит нам более полно оценить значение косинуса и его вклад в решение математических и физических задач.
Косинус угла: что он означает?
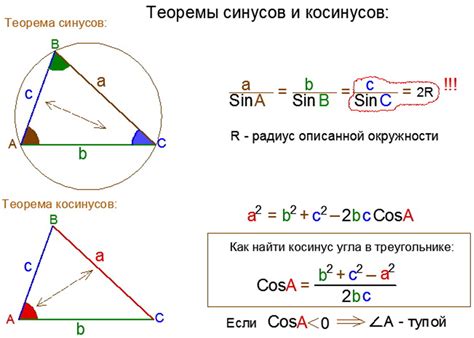
Косинус угла имеет существенное значения не только в геометрии, но и во многих других научных и технических областях. Он помогает решать различные задачи, связанные с измерением углов и расчетом расстояний, а также применяется в физике, инженерии и программировании.
Знание определения косинуса угла и его свойств позволяет выполнять различные вычисления и преобразования, а также решать задачи, связанные с геометрией и тригонометрией. Углы с разными значениями косинуса имеют свои особенности и характеристики, которые становятся полезными при анализе и решении разнообразных задач.
В следующих разделах мы более подробно рассмотрим свойства косинуса угла и методы его вычисления, которые позволят вам легко и точно определить значение косинуса для любого угла.
Интуитивное представление о геометрическом смысле косинуса угла
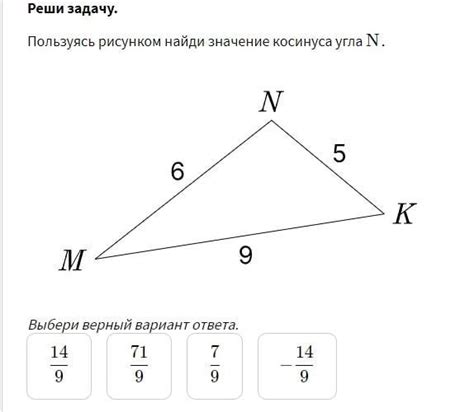
В данном разделе мы рассмотрим интуитивное представление о косинусе угла и его геометрическом смысле. Он позволяет нам понять, как функция косинуса связана с геометрией и может быть использована для вычисления определенных свойств и соотношений в различных задачах.
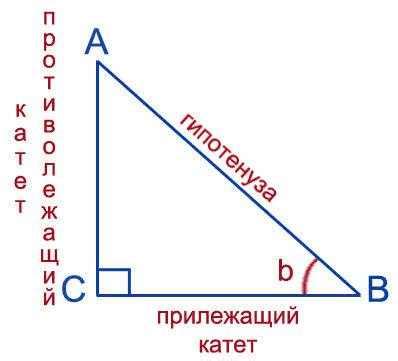
Когда мы говорим о косинусе угла, мы можем помыслить о связи между двумя величинами: длиной гипотенузы и длиной прилегающего к ней катета прямоугольного треугольника. Чем больше угол между этими сторонами, тем меньше длина катета, отложенного на этом угле. Косинус угла представляет собой отношение длины прилегающего катета к длине гипотенузы.
Представим, что мы разместили прямоугольный треугольник на плоскости и угол, для которого мы хотим найти косинус, откладывается от горизонтальной оси. Тогда косинус угла будет определяться отношением горизонтального смещения к гипотенузе. При этом, если угол близок к нулю, горизонтальное смещение будет максимальным и косинус угла будет равен 1. Если угол приближается к 90 градусам, смещение становится минимальным и косинус угла стремится к 0.
Определение косинуса угла через геометрическую интерпретацию позволяет нам легко понимать его значения и связи с геометрическими фигурами. Это имеет широкое применение в физике, инженерии, компьютерной графике и других областях, где необходимо работать с углами и их свойствами.
Применения косинуса угла: важность и области использования
- Механика. Косинус угла находит применение для оценки направленности действующей силы относительно оси, что является основой для определения ее проекции на данную ось. Также косинус угла позволяет вычислить работу, совершаемую силой, и определить ее эффективность.
- Электротехника. Косинус угла становится полезным инструментом при вычислении активной мощности, которая используется в электрических цепях. Это параметр, отражающий степень соответствия между током и напряжением, и позволяет определить эффективность работы электрической системы.
- Физика. В физике косинус угла применяется для определения силы тяжести во векторной форме. Благодаря этому понятию можно вычислить компоненту вектора силы, направленную вдоль определенной оси, что важно при решении многих задач.
- Астрономия. Косинус угла используется для определения высоты, а также для отслеживания движения небесных объектов и планет. Он является ключевым параметром для точного расчета и предсказания положения небесных тел в пространстве.
Эти примеры лишь немногочисленные области, где косинус угла находит применение. Можно смело сказать, что без использования косинуса угла невозможно научное и техническое развитие во многих областях. Понимание и умение применять эту тригонометрическую функцию является необходимым для достижения точных и надежных результатов в решении различных задач.
Тригонометрические функции: понятие и назначение
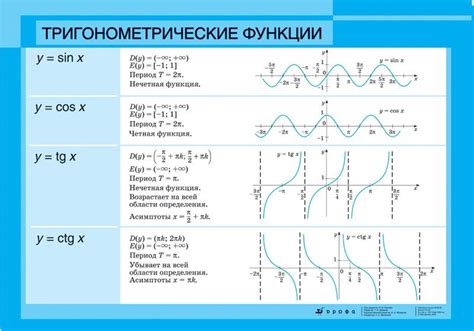
В математике существуют определенные функции, которые связывают углы в треугольниках и их соответствующие стороны. Эти функции называются тригонометрическими. Они играют важную роль в вычислениях и анализе угловых отношений в различных областях, включая физику, инженерные науки и геометрию.
Тригонометрические функции, такие как синус, косинус и тангенс, позволяют измерять и выражать соотношения между углами и сторонами треугольников. Например, косинус угла может быть определен как отношение длины прилегающей катеты к гипотенузе прямоугольного треугольника. Помимо этого, тригонометрические функции также имеют ряд свойств и формул, которые позволяют выполнять различные операции и решать уравнения, связанные с угловыми зависимостями.
Изучение тригонометрических функций является основой для понимания сложных математических концепций и широко применяется в разных областях науки и техники. Поэтому важно иметь представление о понятии и назначении этих функций, чтобы успешно использовать их в расчетах и анализе геометрических объектов и угловых отношений.
Способы определения значения косинуса посредством тригонометрической окружности
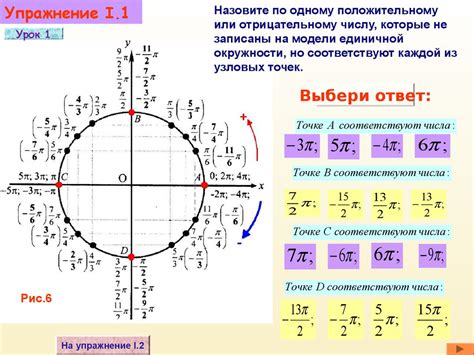
Тригонометрическая окружность представляет собой круг, внутри которого находится точка O - начало направленной отрезковой линии, обозначающей угол. Радиус окружности равен 1, что позволяет упростить вычисления и облегчить понимание.
Существует несколько основных шагов для определения значения косинуса с использованием тригонометрической окружности:
- Выберите угол, значение косинуса которого требуется найти.
- Постройте соответствующую тригонометрическую окружность. Пометьте точку O, соответствующую началу направленной отрезковой линии для выбранного угла.
- Постройте линию, начинающуюся в точке O и проходящую через окружность в направлении, противоположном исходной точке.
- Определите координаты точки пересечения этой линии и окружности. Обозначьте эти координаты как (x, y).
- Значение косинуса угла равно x, так как x-координата точки пересечения является проекцией изначальной точки O на ось X.
Использование тригонометрической окружности обеспечивает интуитивное понимание процесса вычисления косинуса угла и может быть полезным для начинающих студентов. Давая возможность визуализации геометрических соотношений, этот метод помогает уяснить связь между углами и тригонометрическими функциями.
Тригонометрические формулы для вычисления косинуса

В данном разделе мы рассмотрим несколько способов расчета косинуса с помощью тригонометрических формул. На основе этих формул можно получить численное значение косинуса различных углов с высокой точностью.
Идентичность косинуса:
Одной из базовых формул для расчета косинуса является идентичность косинуса, которая устанавливает связь между косинусами суммы и разности двух углов. С использованием этой формулы, можно выразить косинус суммы или разности углов через косинусы и синусы отдельных углов.
Пример:
Пусть даны углы α и β. Тогда для косинуса суммы углов (α + β) справедливо следующее соотношение: cos(α + β) = cos α * cos β - sin α * sin β.
Тригонометрический круг:
Другим способом вычисления косинуса является использование тригонометрического круга. Этот круг представляет собой окружность, на которой заданы значения косинуса и синуса для каждого угла от 0° до 180°. С помощью геометрической интерпретации можно определить значение косинуса для конкретного угла, используя отношение длин сторон прямоугольного треугольника, образованного углом и радиусом окружности.
Пример:
Пусть требуется определить косинус угла 45°. Для этого мы можем построить прямоугольный треугольник на тригонометрическом круге и использовать отношение катета к гипотенузе, что равносторонний треугольник со стороной 1, чтобы определить значение косинуса.
Использование калькулятора или онлайн калькулятора для вычисления косинуса
В данном разделе мы рассмотрим возможные способы расчета значения косинуса угла, при которых можно воспользоваться обычным калькулятором или онлайн калькулятором. Эти инструменты позволяют быстро и точно определить значение косинуса без необходимости использования сложных математических формул и процедур.
| Способ расчета | Описание |
|---|---|
| Использование обычного калькулятора | Для вычисления косинуса угла с помощью обычного калькулятора необходимо ввести значение угла в градусах или радианах, воспользоваться функцией косинуса, после чего нажать на кнопку "равно". Получившийся результат будет являться значением косинуса данного угла. |
| Использование онлайн калькулятора | Если у вас нет обычного калькулятора под рукой или вы предпочитаете использовать онлайн инструменты, то вы можете воспользоваться специальными онлайн калькуляторами для вычисления косинуса угла. Для этого нужно ввести значение угла, выбрать единицу измерения (градусы или радианы) и нажать на кнопку "вычислить". Результат будет выведен на экран в виде числа, представляющего значение косинуса. |
Использование калькулятора или онлайн калькулятора является удобным и простым способом получить точное значение косинуса угла без необходимости проводить сложные вычисления вручную. Эти инструменты особенно полезны при работе с большими числами или при выполнении множества расчетов, где точность и скорость играют важную роль.
Применение косинуса угла в реальной жизни
Использование косинуса угла в повседневной жизни помогает в решении различных задач, связанных с геометрией и физикой. Концепция косинуса угла находит применение в различных областях, таких как архитектура, навигация, физика, компьютерная графика и даже спорт.
Архитектура и строительство: Косинус угла позволяет архитекторам и инженерам определить наклоны, углы и направления при проектировании и строительстве зданий. Он помогает рассчитать нагрузки на конструкции, определить углы наклона крыши или крена здания и провести правильную локализацию строительных объектов.
Навигация и геодезия: Косинус угла используется в навигации и геодезии для определения пути и направления. Это помогает при построении карт и навигационных систем, а также в определении координат и расстояний между точками на земной поверхности.
Физика и инженерия: Косинус угла находит применение во многих разделах физики и инженерии. Он используется для расчетов силы трения и наклона плоскости, а также для определения компонентов векторов силы и момента.
Компьютерная графика и игры: Косинус угла играет важную роль в компьютерной графике и создании игр. Он помогает определить освещение и тени на 3D-моделях, а также при расчете пролетает ли один объект за другим.
Спорт и фитнес: Косинус угла применяется в спорте и фитнесе при анализе движений и позиционирования тела. Он используется для измерения углов сгибания и разгибания в суставах при изучении биомеханики движений и оптимизации тренировок.
Все эти примеры демонстрируют, что знание и использование косинуса угла в реальной жизни имеет широкое применение и может помочь в решении различных задач и проблем в различных областях.
Вопрос-ответ

Можете объяснить, что такое косинус угла?
Косинус угла - это одно из значений тригонометрической функции, которая определяется отношением прилегающего катета к гипотенузе прямоугольного треугольника.
Какие есть способы расчета косинуса угла?
Существует несколько способов расчета косинуса угла. Один из простых способов - использование таблицы значений тригонометрических функций. Также можно вычислить косинус угла с помощью калькулятора, используя встроенные функции. Еще один способ - применение тригонометрических формул, основанных на определении косинуса через синус или на основе многочленов Чебышева.
Как можно использовать косинус угла в реальной жизни?
Применение косинуса угла в реальных задачах весьма разнообразно. Например, косинус угла может использоваться в геодезии для определения высоты точки по измерению угловых отклонений. Он также применяется в физике при расчете напряжений в системе сил или в программировании для работы с трехмерной графикой и анимацией.
Как вычислить косинус угла, если известны значения других тригонометрических функций?
Если известны значения других тригонометрических функций, то косинус угла можно вычислить с помощью формулы, связывающей эти функции. Например, косинус угла можно выразить через синус и тангенс согласно следующим формулам: cos(x) = sin(90 - x) = 1 / tan(x).



