Все мы привыкли воспринимать ромб как геометрическую фигуру, у которой известны его стороны и диагонали. Но что делать, когда известны лишь диагонали, а сторона ромба скрыта где-то в этой геометрической загадке?
Не отчаивайтесь! В этой статье мы поможем вам разгадать эту загадку и обрести недостающую информацию о стороне ромба через его диагонали.
Небольшое введение в основы геометрии пригодится каждому в повседневной жизни. Ведь умение находить недостающие параметры фигур помогает строить качественные планы, прогнозировать результаты и решать самые неожиданные задачи. На этом этапе мы откроем вам один из секретов геометрии - нахождение стороны ромба при известных диагоналях.
Особенности и понятие ромба
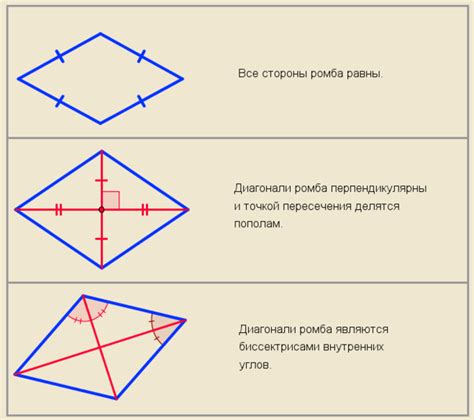
Важно отметить, что при изучении ромба часто интерес представляет не только его форма, но и различные размеры и углы, которые можно определить с помощью геометрических вычислений. Например, один из основных параметров ромба - его стороны. Зная длину одной стороны ромба, можно вычислить все остальные стороны, так как все они равны друг другу. Каким образом устанавливается длина стороны ромба через его диагонали, можно узнать из соответствующего раздела данной статьи.
| Формула рассчета стороны ромба: | S = √((D1/2)^2 + (D2/2)^2) |
Диагонали ромба и их свойства
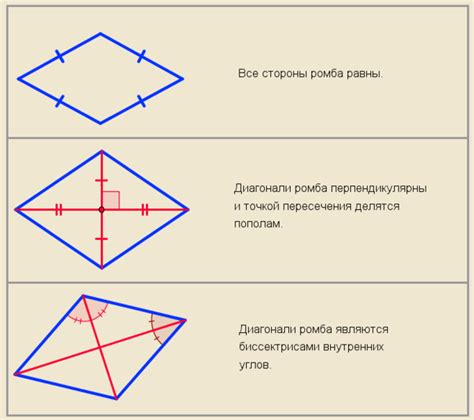
Первое свойство диагоналей ромба заключается в том, что они перпендикулярны друг другу. Это означает, что угол между диагоналями равен 90 градусам. Именно этот угол является особым и создает ряд интересных возможностей для изучения геометрических характеристик ромба.
Второе свойство диагоналей заключается в том, что они делят ромб на четыре равные треугольные формы. Если рассмотреть ромб как композицию таких треугольников, то можно увидеть, что каждая диагональ является осью симметрии для соответствующего треугольника. Это дает нам возможность использовать свойства треугольников для определения других характеристик ромба.
Третье свойство диагоналей связано с соотношением между диагоналями и сторонами ромба. Если обозначить длину стороны ромба как a, а длину диагоналей как d1 и d2, то справедливо следующее соотношение: d1 = a * √2 и d2 = a * √2. Из этой формулы мы можем найти длину стороны ромба, зная длины его диагоналей.
В данном разделе мы рассмотрели основные свойства диагоналей ромба и их влияние на другие характеристики этой геометрической фигуры. Изучив эти свойства, можно легко определить сторону ромба, зная длины его диагоналей.
Вычисление длины стороны ромба на основе его диагоналей

В данном разделе мы рассмотрим метод определения длины стороны ромба, используя информацию о его диагоналях. Этот подход позволяет нам получить точное значение стороны ромба, основываясь на известных длинах диагоналей, без необходимости знать другие параметры фигуры.
Для начала нам потребуется определить синус угла, образованного диагоналями ромба. Мы можем воспользоваться тригонометрическим соотношением, где синус угла равен отношению половины произведения длин диагоналей к их произведению:
sin(α) = (d1 * d2) / (2 * d1 * d2)
Здесь α - угол, образованный диагоналями, d1 и d2 - длины диагоналей ромба. Зная значение синуса угла, мы можем выразить длину стороны ромба через длины диагоналей, используя простую тригонометрическую формулу:
a = 2 * sqrt((d1 * d2) / (sin(α)))
Где a - длина стороны ромба. Теперь, имея данную формулу, вы можете легко вычислить длину стороны ромба, используя известные значения диагоналей. Учтите, что величина альфа должна быть измерена в радианах, поэтому перед использованием формулы вам может потребоваться конвертировать угол из градусов в радианы.
Узнаем размер одной стороны ромба с помощью известных диагоналей
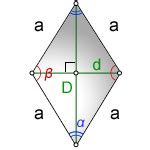
В этом разделе мы рассмотрим несколько примеров, которые помогут вам определить длину одной стороны ромба, исходя из известных значений его диагоналей. Решение этой задачи позволит вам строить и анализировать ромбы в различных сферах, включая геометрию, строительство и проектирование.
Перед тем как приступить к примерам, давайте вспомним, что ромб - это четырехугольник, у которого все стороны равны друг другу. У него также есть две диагонали, которые пересекаются под прямым углом. Используя формулы и некоторые геометрические свойства, мы сможем получить нужные нам значения.
- Пример 1: Найдем сторону ромба, если известны его две диагонали: D1 = 10 см и D2 = 8 см.
- Пример 2: Рассчитаем длину стороны ромба по значениям его диагоналей: D1 = 12 м и D2 = 9 м.
- Пример 3: Измерим одну из сторон ромба, зная его диагональ D1 = 15 дм и длину перпендикуляра, опущенного на диагональ, равную 12 дм.
Приступим к решению каждого из примеров по порядку, используя соответствующую формулу для вычисления стороны ромба через диагонали. Следуйте указанным шагам и вы получите решение к каждой задаче!
Значимость знания размера стороны ромба в реальной жизни
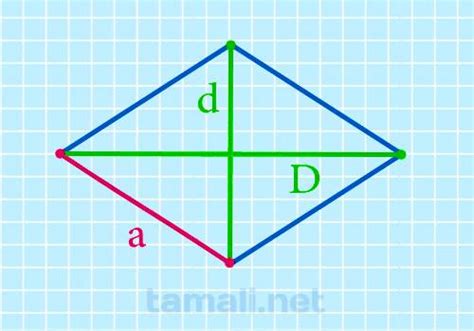
Размер стороны ромба является важной характеристикой в строительстве, например, при планировании и построении фундамента или крыши. Использование правильных размеров ромба позволяет обеспечить устойчивость и прочность конструкции, а также достичь эстетического и гармоничного вида здания.
В дизайне и графике знание размеров стороны ромба помогает создавать симметричные и элегантные композиции. Использование ромбовых форм в украшениях, логотипах, визуальных эффектах и архитектурных элементах придает проекту индивидуальность и выразительность.
Некоторые виды спорта также включают элементы ромбовой формы. Например, баскетбольное или волейбольное поле имеет форму ромба, и точное знание его размеров позволяет игрокам и тренерам эффективно планировать тактику и стратегию.
Альтернативные подходы к нахождению длины стороны ромба, исходя из известных диагоналей

В этом разделе мы рассмотрим некоторые альтернативные методы для определения длины стороны ромба, основываясь на уже известных диагоналях. Вместо использования стандартных формул и прямолинейных алгоритмов, мы исследуем несколько нетривиальных подходов, позволяющих получить точные результаты и расширить наше понимание геометрии ромба.
1. Метод равенства длин дуг, соединяющих середины сторон ромба. В этом методе мы используем свойство ромба, согласно которому дуги, соединяющие середины сторон ромба, имеют одинаковую длину. Измеряем длину каждой из этих дуг при помощи геометрического инструмента и уравниваем полученные значения, чтобы определить длину стороны ромба. Этот метод особенно полезен, когда нам известны диагонали, но отсутствуют другие данные о ромбе.
2. Метод использования теоремы Пифагора для треугольника в ромбе. В этом методе мы используем связь между диагоналями ромба и его сторонами, которую можно выразить через теорему Пифагора для треугольника в ромбе. Используя известные значения диагоналей, мы можем вывести уравнения, содержащие длины сторон ромба. Решая эти уравнения, мы получаем точные значения сторон.
3. Метод проведения высоты, опущенной из вершины ромба. Этот метод основан на использовании геометрического свойства ромба, согласно которому биссектриса внешних углов ромба перпендикулярна стороне ромба. Проводим высоту из одной из вершин ромба и измеряем ее длину. Затем, используя полученное значение, мы можем вывести уравнения, связывающие длину стороны ромба и диагонали. Решая эти уравнения, мы определяем длину стороны ромба исходя из данных о диагоналях.
Важные соображения при применении математической формулы

Использование формул в математике может быть сложной задачей, требующей внимательного рассмотрения и определенных соображений. При использовании формулы для определения стороны ромба через его диагонали, есть несколько ключевых аспектов, на которые следует обратить внимание, чтобы получить точный ответ.
Во-первых, необходимо убедиться, что диагонали ромба уже известны и правильно измерены. Неточные или ошибочные измерения могут привести к неверным результатам. Поэтому рекомендуется использовать точные инструменты для измерения диагоналей, такие как линейка или штангенциркуль.
Во-вторых, формула, используемая для определения стороны ромба через его диагонали, должна быть правильно понята и применена. Важно понимать, какие переменные и значения используются в формуле, чтобы избежать путаницы и ошибок. Также следует обратить внимание на порядок операций и правильность расчетов, чтобы получить точные результаты.
Кроме того, при использовании формулы для нахождения стороны ромба через его диагонали, необходимо учитывать особенности ромба как геометрической фигуры. Ромб имеет свои уникальные свойства, такие как равенство диагоналей и перпендикулярность сторон, которые можно использовать для дополнительных вычислений или проверки правильности полученных результатов.
Наконец, всегда рекомендуется проверять полученные результаты и сравнивать их с другими методами измерения или вычисления. Это поможет убедиться в точности результатов и обнаружить возможные ошибки или неточности. При необходимости, можно повторить расчеты или использовать альтернативные подходы для подтверждения полученных значений.
Вопрос-ответ

Как найти сторону ромба, если известны диагонали?
Для нахождения стороны ромба по диагоналям можно использовать формулу "s = √(d₁² + d₂²) / 2", где "s" - сторона ромба, "d₁" и "d₂" - диагонали. Для этого нужно возвести квадратами значения диагоналей, сложить их, извлечь квадратный корень и поделить на 2.
Как найти длину стороны ромба по известным диагоналям 12 и 16?
Для нахождения длины стороны ромба по диагоналям 12 и 16 можно использовать формулу "s = √(12² + 16²) / 2". Подставим значения и произведем вычисления: s = √(144 + 256) / 2 = √400 / 2 = 20 / 2 = 10. Таким образом, длина стороны ромба равна 10.
Как найти длину стороны ромба, если известны диагонали равные 9 и 12?
Для нахождения длины стороны ромба по диагоналям 9 и 12 нужно использовать формулу "s = √(9² + 12²) / 2". Подставим значения и выполним вычисления: s = √(81 + 144) / 2 = √225 / 2 = 15 / 2 = 7.5. Таким образом, длина стороны ромба равна 7.5.



