Один из самых захватывающих объектов в мире математики - шар. Его безукоризненная форма идеально симметрична, призывая ученых и любопытных умов погрузиться в его тайны. Изучение шара имеет огромное практическое значение, способствуя решению различных проблем и задач в различных областях науки и техники.
Но как точно определить и рассчитать площадь этого загадочного объекта? Радиус шара и его поверхность содержат множество интересных сведений и формул, которые могут быть применены для вычислений. Понимание этих концепций открывает перед нами удивительный мир геометрии и математического моделирования.
В этом основополагающем руководстве мы рассмотрим различные методы и примеры для рассчета площади шара. У вас появится возможность глубже погрузиться в мир многомерного пространства, забыться в прелесть математических выкладок и, конечно же, научиться применять полученные знания на практике.
Что представляет собой площадь шара и какая роль ей отведена?

Площадь шара является мерой его поверхности, а не объема. Она представляет собой общую площадь внешней поверхности шара без учета его внутреннего содержимого. Знание площади шара может быть полезно, например, при проектировании сферических сооружений, какими могут быть купола, башни или емкости. Также она является важной характеристикой для геометрии и физики.
Определение площади шара позволяет проводить расчеты и прогнозировать поведение шарообразных тел в различных ситуациях. Например, зная площадь шара и его массу, можно оценить теплопередачу или прочность материала шара. В медицине площадь поверхности шарообразных органов может использоваться для определения дозы лекарственных препаратов или облучения в радиотерапии.
Таким образом, понимание площади шара и ее значения играет важную роль в различных областях науки и практики. Она помогает проводить анализ, расчеты и прогнозы, а также принимать взвешенные решения на основе полученных данных. Продолжайте чтение, чтобы узнать, как рассчитать площадь шара и применить эту информацию на практике.
Роль площади шара в математике и геометрии
Определение площади шара основывается на его форме и особенностях. Поверхность шара является сферической, что означает, что в одной точке данной поверхности касание или пересечение с другой точкой образуют сферическое тело, равное сферической поверхности. Площадь шара измеряется в квадратных единицах, таких как квадратные метры или квадратные сантиметры.
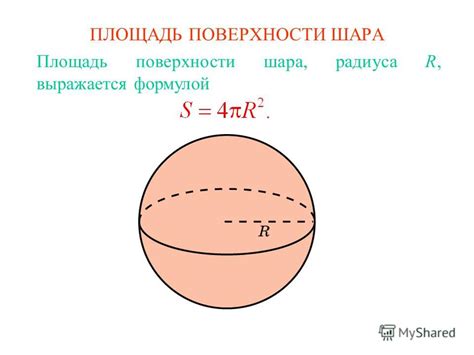
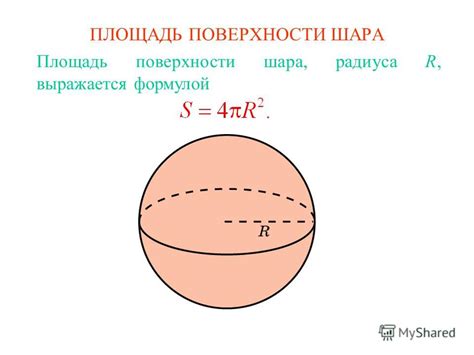
Для определения площади шара существует ряд методов, которые могут быть использованы в зависимости от доступной информации и требуемой точности результата. Например, если мы знаем радиус шара, мы можем использовать формулу, основанную на уравнении поверхности шара: S = 4πr², где S - площадь поверхности шара, а r - радиус.
Разумное понимание площади шара и способов ее определения имеет множество применений. В архитектуре и дизайне площадь шара может быть важной величиной при расчете объема некоторых конструкций или пространств. В аэродинамике и авиации площадь шара может использоваться для моделирования и предсказания поведения тела в плотном воздухе или в пространстве. Это лишь некоторые примеры применения площади шара, демонстрирующие ее значимость в различных областях науки и технологий.
Формула для вычисления площади поверхности шара в зависимости от его радиуса
В данном разделе мы рассмотрим формулу для определения площади поверхности шара на основе известного значения его радиуса. Используя эту формулу, вы сможете легко вычислить площадь шара без необходимости проведения дополнительных измерений или сложных вычислений.
Формула для расчета площади поверхности шара основана на его геометрических свойствах. Шар является трехмерным объектом, который состоит из бесконечного количества точек, находящихся на одинаковом расстоянии от его центра. Если мы возьмем любую точку на поверхности этого шара и проведем линию от этой точки до центра шара, то получим радиус - это расстояние от центра шара до его поверхности. Площадь поверхности шара представляет собой сумму площадей всех его точек, которые находятся на равном расстоянии от его центра.
Для вычисления площади поверхности шара необходимо знать его радиус - это расстояние между центром шара и его поверхностью. Правильная формула для расчета площади шара по его радиусу выглядит следующим образом:
- Умножьте число Пи (π) на значение радиуса в квадрате;
- Точное значение числа Пи можно взять равным 3,14 или округлить его до определенного количества знаков после запятой;
- Полученное произведение будет являться площадью поверхности шара.
Теперь, имея формулу, вы можете легко рассчитать площадь поверхности шара, зная только его радиус. Например, если радиус шара равен 5 сантиметрам, то площадь поверхности шара будет равна 3,14 * (5^2) = 3,14 * 25 = 78,5 квадратных сантиметров.
Подробное описание формулы для вычисления поверхности шара, с доказательством ее корректности
Этот раздел посвящен детальному описанию формулы для расчета площади поверхности шара, где мы представим ее происхождение и докажем ее верность. Результаты вычислений позволят нам определить общую площадь поверхности шара с помощью данной формулы.
Для начала рассмотрим геометрические особенности шара. Шар - это геометрическое тело, состоящее из всех точек, равноудаленных от его центра. Поверхность шара представляет собой сферу, которая образуется при повороте окружности вокруг ее диаметра. Наша цель - вычислить площадь этой поверхности.
Формула для вычисления площади поверхности шара установлена и носит название "формула поверхности шара". Она основана на математических принципах и теоремах.
Формула поверхности шара имеет вид: S = 4πR^2, где S представляет собой площадь поверхности шара, π (пи) - математическая константа, примерное значение которой равно 3.14159, и R обозначает радиус шара.
Доказательство верности данной формулы основывается на геометрической интерпретации приращений площади поверхности шара при изменении радиуса. Мы можем разделить поверхность шара на бесконечно малые элементы площади, подобные треугольникам или колоссально увеличенным на конечную величину разделить на некоторое количество треугольников, и затем суммировать их площади. Получившуюся сумму можно аппроксимировать, а в пределе получить точную площадь поверхности шара. Это доказывает верность формулы S = 4πR^2.
Примеры вычисления площади сферы

В данном разделе мы рассмотрим несколько примеров, иллюстрирующих процесс расчета площади шара. Описанные ниже случаи помогут вам лучше понять, как получить значение площади сферы, используя различные методы и формулы.
Первый пример представляет собой классический способ вычисления площади шара с помощью радиуса. Мы рассмотрим формулу и пошаговый алгоритм, который поможет вам осуществить подсчет вручную.
Второй пример посвящен использованию численных методов, таких как интегрирование методом Монте-Карло, для приближенного вычисления площади сферы. Вы узнаете, как генерировать случайные точки вокруг сферы и использовать их для оценки ее площади.
Третий пример представляет собой применение специальных формул и уравнений для расчета площади определенных типов шаров, таких как полый шар или сегмент сферы. Мы рассмотрим математические выкладки и описания каждого случая.
Итак, следуя данным примерам, вы получите возможность углубиться в процесс вычисления площади шара, используя разные подходы и методы расчета. Это позволит вам лучше понять геометрические принципы, связанные с данной задачей, и научиться применять их на практике.
Практические задачи с детальным разбором расчета площади поверхности шара
Для лучшего понимания процесса расчета площади шара, давайте рассмотрим несколько разнообразных практических примеров с подробным объяснением каждого шага. Мы использовать различные методики и формулы, чтобы наглядно продемонстрировать, как определить площадь поверхности данной геометрической фигуры.
| Пример | Задача | Решение |
|---|---|---|
| Пример 1 | Найти площадь поверхности шара с радиусом 5 см | 1. Используем формулу площади поверхности шара: S = 4πr² |
| Пример 2 | Рассчитать площадь шара, зная его объем | 1. Используем формулу объема шара: V = (4/3)πr³ 2. Находим радиус шара, используя известный объем и формулу |
| Пример 3 | Решить задачу на определение площади шара с половинным радиусом | 1. Используем свойства геометрической фигуры 2. Применяем соответствующую формулу для нахождения нужной площади |
| Пример 4 | Расчет площади шарового отсека, зная радиусы двух шаров | 1. Рассчитываем площади поверхностей двух сфер 2. Вычитаем площадь отсека одной сферы из площади поверхности другой сферы |
| Пример 5 | Задача на построение шарового сегмента и расчет его площади | 1. Вычисляем угол открытого сегмента по заданным данным 2. Строим сегмент на графике с использованием радиуса и угла |
Надеемся, что представленные примеры помогут вам разобраться в процессе расчета площади поверхности шара и применить полученные знания на практике. Важно понимать каждый шаг и уметь адаптировать формулы для различных задач, связанных с геометрией шара.
Сопоставление между объемом и поверхностной площадью шара
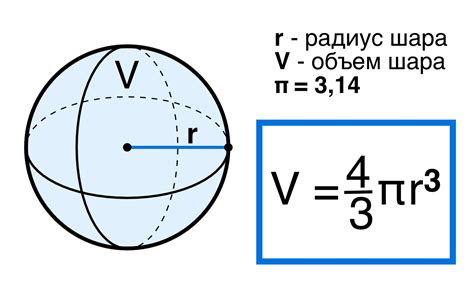
Объем шара - это мера, которая определяет, сколько пространства занимает шар. Он выражается в кубических единицах (например, кубические сантиметры или кубические метры) и рассчитывается с использованием соответствующей формулы.
С другой стороны, поверхностная площадь шара - это мера, которая определяет, сколько площади занимает поверхность шара. Она выражается в квадратных единицах (например, квадратные сантиметры или квадратные метры) и также рассчитывается с помощью соответствующей формулы.
Следует отметить, что существует связь между объемом и поверхностной площадью шара. Если увеличить радиус шара, то его объем будет увеличиваться быстрее, чем поверхностная площадь. И наоборот, если уменьшить радиус, объем будет уменьшаться быстрее, чем поверхностная площадь.
| Обозначение | Формула | Описание |
|---|---|---|
| V | 4/3 * π * r³ | Объем шара |
| S | 4 * π * r² | Поверхностная площадь шара |
Здесь формула для объема шара использует радиус (r) шара, а формула для поверхностной площади шара также использует радиус (r).
Понимание связи между объемом и поверхностной площадью шара важно при решении задач, связанных с этими параметрами и их изменениями. На основе этих связей математики и инженеры могут оптимизировать форму и размеры шарообразных объектов для достижения желаемых характеристик и удовлетворения конкретных требований.
Объяснение взаимосвязи между площадью и объемом шара с примерами для большего понимания

Представим, что у нас есть шар с радиусом R. Площадь шара можно рассчитать по формуле S = 4πR², где π (пи) является математической константой, приближенно равной 3,14. Эта формула широко используется для определения площади замкнутой поверхности шара. Чем больше радиус шара, тем больше его площадь поверхности.
Теперь перейдем к объему шара. Для его расчета применяется формула V = (4/3)πR³, где π (пи) также примерно равно 3,14. Эта формула позволяет определить, сколько пространства занимает шар внутри своей поверхности. Объем шара также зависит от его радиуса - чем больше радиус, тем больше объем.
Рассмотрим пример, чтобы проиллюстрировать взаимосвязь между площадью и объемом шара. Представим два шара с одинаковым радиусом - R. Площадь первого шара будет S1 = 4πR², а объем V1 = (4/3)πR³. Теперь возьмем второй шар с радиусом 2R. Площадь второго шара будет S2 = 4π(2R)² = 4π*4R² = 16πR², а его объем V2 = (4/3)π(2R)³ = (4/3)π8R³ = 32πR³. Из этого примера видно, что увеличение радиуса шара приводит к увеличению его площади и объема в соответствии с соответствующими формулами.
Таким образом, понимание взаимосвязи между площадью и объемом шара позволяет более глубоко изучать и анализировать свойства этой геометрической фигуры. Зная радиус, мы можем легко рассчитать площадь и объем шара, что является важной информацией в различных математических и научных задачах.
Применение площади шара в повседневной жизни

Площадь поверхности шара имеет широкий спектр применения в различных сферах нашей жизни. Благодаря этому параметру мы можем решать множество задач и применять его для решения практических проблем.
В медицине площадь шара используется при расчете дозировки лекарств. Зная площадь поверхности человеческого органа, врачи могут предсказать скорость распределения лекарственных веществ и определить оптимальную дозировку для достижения требуемого эффекта.
В архитектуре площадь шара играет важную роль при проектировании куполов и куполообразных конструкций. Зная площадь поверхности, архитекторы могут определить необходимое количество материалов для возведения сооружения и спланировать его внутреннее пространство.
В географии площадь шара используется при изучении земного шара и его характеристик. Зная площадь поверхности Земли, ученые могут определять изменения климата, изучать границы между материками и океанами, а также анализировать влияние географических особенностей на экологию планеты.
Кроме того, знание площади шара может быть полезно в повседневной жизни. Например, при планировании покупки или ремонта мебели, зная площадь поверхности шара, можно определить, сколько ткани или обоев потребуется для покрытия поверхности предмета.
Таким образом, площадь шара является важным параметром, который находит применение в разных областях нашей жизни. Знание этого понятия позволяет решать различные задачи, оптимизировать процессы и принимать взвешенные решения в различных сферах деятельности.
Применение площади шара в различных областях науки и технологий

- Астрономия: Вычисление площади поверхности планеты или других небесных тел позволяет определить их размеры и характеристики.
- Металлургия: Знание площади поверхности шарообразных объектов, таких как шары для производства подшипников или шаровые краны, помогает определить необходимый объем материала для их изготовления.
- Фармакология: Площадь поверхности лекарственных сферических гранул и капсул влияет на скорость растворения и эффективность их действия внутри организма.
- Косметология: Расчет площади поверхности сферических частиц в косметических средствах используется для оценки их способности поглощать излишки себума или других веществ с кожи.
- Физика: Знание площади поверхности шара позволяет определить его момент инерции и другие физические характеристики.
- 3D-моделирование: Расчет площади поверхности 3D-модели шарообразных объектов используется для оптимизации текстурных карт и распределения материалов на поверхности модели.
Вышеуказанные примеры демонстрируют, что площадь шара имеет широкий спектр практического применения в различных областях науки и технологий. Нахождение этой характеристики позволяет решать разнообразные задачи, от определения размеров небесных тел до оптимизации текстур в 3D-моделях. Это лишь несколько примеров из множества сфер, где площадь шара играет важную роль и находит свое практическое применение.
Вопрос-ответ

Как рассчитать площадь шара?
Для расчета площади шара необходимо знать его радиус. Формула для расчета площади поверхности шара выглядит так: S = 4πR², где S - площадь поверхности шара, π - математическая константа (приблизительно равна 3,14), R - радиус шара. Умножив квадрат радиуса на 4π, вы получите площадь поверхности шара.
Есть ли какие-то примеры расчета площади шара?
Да, конечно. Допустим, у вас есть шар с радиусом 5 см. Чтобы рассчитать его площадь поверхности, нужно воспользоваться формулой S = 4πR². Подставляя значение радиуса, получаем: S = 4 * 3,14 * (5)² = 4 * 3,14 * 25 = 314 см². Таким образом, площадь поверхности шара равна 314 квадратных сантиметров.
Можно ли расчитать площадь шара, если известен диаметр?
Да, это возможно. Если известен диаметр шара, то для расчета площади поверхности нужно сначала найти радиус. Для этого диаметр нужно поделить на 2. Затем, используя формулу S = 4πR², можно вычислить площадь поверхности, подставив найденное значение радиуса в формулу.



