В семидесятые годы прошлого века, когда программирование только начинало зарождаться, математики и разработчики сталкивались с непростой задачей нахождения значений функций с высокой точностью. Оценка сложности вычислений и выбор подходящего метода решения могли занять дни или даже недели. Однако, с развитием технологий и появлением новых математических алгоритмов, этот процесс стал не только более эффективным, но и легким в реализации.
Сейчас, благодаря набору инструментов и библиотек, нахождение значений функции приобретает новое измерение - оно становится интуитивным и доступным. Алгоритмы определения функций на основе вводных данных, а также итеративные методы вычисления значений стали неотъемлемой частью программного обеспечения различных областей науки и техники.
Однако, несмотря на то, что набор современных инструментов значительно упрощает решение данной проблемы, необходимость аккуратной настройки параметров и правильного выбора алгоритма все еще остается темой для исследования и улучшения. В данной статье мы рассмотрим простые и эффективные способы нахождения значений функций, которые с легкостью справляются с необходимыми вычислениями. В числе этих методов можно выделить использование разнообразных численных алгоритмов, аппроксимационные модели, а также применение специализированных математических пакетов и библиотек.
Исследуем функцию: понимаем ее значение без лишних усилий
При решении математических задач зачастую возникает необходимость нахождения значения функции. Это ключевой момент в понимании и анализе функциональных систем. Однако, простой подход к определению значения функции может значительно упростить процесс и сделать его более доступным даже для тех, кто не обладает глубоким математическим подходом.
Вместо того, чтобы использовать сложные формулы и расчеты, простой способ нахождения значения функции позволяет основываться на интуитивном понимании функций и их свойствах. Этот метод предлагает использовать разнообразные методы и идеи, которые помогают нам более общими способами понять, как функции меняются в различных ситуациях.
Так, например, вместо того, чтобы вычислять точное значение функции в определенной точке, можно использовать аналитические и графические методы для определения ее поведения в окрестности этой точки. Таким образом, мы можем получить представление о характере изменения функции, ее максимальных и минимальных значений и прочих ключевых особенностях, без необходимости в точном значении в конкретном месте.
Важно отметить, что этот простой способ является гибким и интуитивным. Он позволяет не только быстро получить общее представление о функции, но и легко проводить анализ и сравнение различных функций. Благодаря этому, метод нахождения значения функции становится доступным инструментом для любого, кто интересуется работой функциональных систем.
Определение значения функции
Для каждого значения аргумента функция может принимать уникальное значение, которое может быть каким-то числом, буквой, словом или другой символьной комбинацией. Значение функции может быть представлено как результат вычисления выражения, описывающего данную функцию. Это значение помогает понять, как функция меняется в зависимости от изменения аргументов и как она связана с другими функциями.
| Термин | Описание |
|---|---|
| Значение функции | Результат, получаемый при подстановке определенного аргумента в функцию |
| Аргумент | Значение, которое подставляется в функциональное выражение |
| Выражение | Математическое или логическое выражение, описывающее функцию |
Определение функции и ее особенности

Первой особенностью функции является ее определенность. Функция может быть определена аналитически или графически. Аналитическое определение функции заключается в задании формулы или алгоритма, с помощью которых можно получить выходное значение функции из заданного входного значения. Графическое определение функции представляет собой набор точек на координатной плоскости, где каждая точка соответствует паре входного и выходного значения функции.
Второй особенностью функции является ее однозначность. Функция является однозначной, если каждому входному значению соответствует только одно выходное значение. В то же время, функция может быть многозначной, когда одному входному значению соответствует несколько выходных значений.
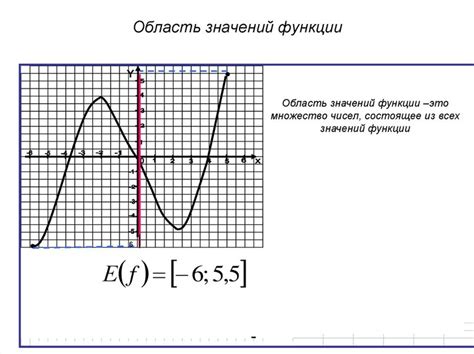
Третьей особенностью функции является ее область определения и область значений. Область определения – это множество всех входных значений, для которых функция имеет определенное значение. Область значений – это множество всех выходных значений, которые может принимать функция.
Наконец, четвертой особенностью функции является ее график. График функции – это геометрическое представление функции на координатной плоскости. График позволяет визуально представить изменение выходного значения функции относительно входного значения и обнаружить особенности, такие как экстремумы, перегибы и т.д.
Причина крайне необходимого знания значения математической зависимости

Знание значений функций имеет решающее значение в различных областях человеческой деятельности, будь то финансовый анализ, физические расчеты, прогнозирование роста и развития процессов или даже решение бытовых задач. Зная значения функций, мы можем оценить, как будут вести себя процессы, и определить оптимальные решения для достижения желаемых результатов.
В экономике, знание функций позволяет анализировать рынки и прогнозировать цены на товары и услуги. Зная значение функции спроса, можно определить, как изменится общий спрос на определенное количество товара в случае изменения его цены или других факторов, таких как доход покупателя или цены сопутствующих товаров. | В физике и инженерии, знание функций позволяет проводить различные расчеты, например, предсказывать траекторию движения тела, оценивать энергию и мощность системы или определять, как изменится скорость распространения волны при взаимодействии среды. |
Знание функций также имеет практическое значение в процессе принятия решений в быту. Например, зная зависимость между стоимостью проживания и доходом, можно более осознанно планировать свои финансы и принимать решения о смене работы или переезде в другой город или страну. |
Идентификация результатов функции через простой алгоритм
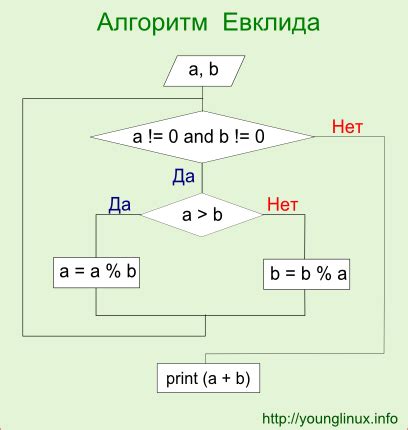
В данном разделе рассматривается эффективный метод определения конечных значений функции с помощью простого алгоритма. Представленный подход позволяет получить результаты функции без сложных вычислений, используя простые шаги.
Для начала, следует определить основные параметры функции, включая аргументы и область определения. Далее, используя заданные значения аргументов, можно приступить к вычислению значения функции. Данный алгоритм предлагает упрощенную итеративную процедуру для получения этих результатов.
| Шаг | Действие | Результат |
|---|---|---|
| 1 | Выбрать начальное значение аргумента | Задать значение для основного аргумента функции |
| 2 | Подставить значение аргумента в функцию | Получить промежуточный результат |
| 3 | Проверить условие достижения конечного значения | Оценить, достигнут ли конечный результат |
| 4 | Если условие не достигнуто, перейти к следующему шагу | Продолжить итерацию для получения более точных результатов |
| 5 | Если условие достигнуто, закончить выполнение алгоритма | Определить конечное значение функции |
Таким образом, данный простой алгоритм позволяет быстро и эффективно идентифицировать значения функции, не требуя сложных математических операций. Он особенно полезен, когда точное значение может быть найдено после оценки достаточного числа итераций.
Описание шагов алгоритма и их разъяснение
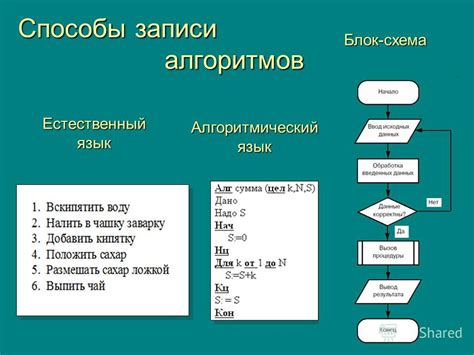
Раздел "Шаги алгоритма и их объяснение" представляет собой последовательное описание операций, необходимых для нахождения значения функции. В данном разделе рассматриваются конкретные шаги, их особенности и объяснение применяемых понятий и методов.
- Изучение задачи и определение условий.
- Анализ функции и ее основных свойств.
- Выбор подходящего метода решения.
- Проведение вычислений и применение алгоритма.
- Проверка результатов и их интерпретация.
Первым шагом является внимательное прочтение задачи и понимание поставленных условий. Для успешного решения задачи необходимо четкое представление о том, как функция связана с входными данными и какие параметры следует учесть.
На этом шаге происходит более детальное изучение функции, выявление ее основных свойств и закономерностей. Особое внимание уделяется анализу области определения, области значений, а также возможных ограничений функции.
После анализа функции выбирается подходящий метод решения, исходя из специфики задачи и доступных математических инструментов. Метод может быть аналитическим или численным, и для его выбора необходимо учитывать сложность функции и требуемую точность результатов.
На этом шаге выполняются вычисления с использованием выбранного метода решения. Применяется алгоритм, который включает в себя необходимые математические операции и последовательность действий для получения значения функции.
Примеры: вычисление результата функциональной зависимости
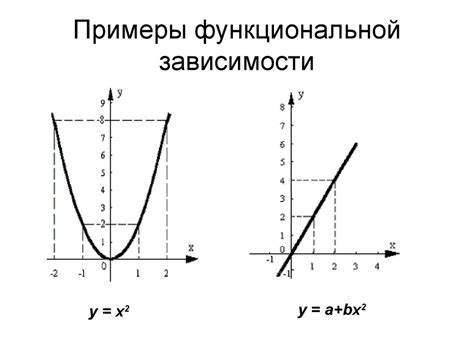
В этом разделе представлены иллюстративные примеры вычисления решений функциональных зависимостей. Здесь мы рассмотрим различные контексты, в которых возникают такие функции, и приведем примеры их расчетов.
| Пример 1 | Пример 2 | Пример 3 |
|---|---|---|
| Вычисление значений функции в математическом анализе | Определение значения функции в программировании | Вычисление результирующего значения в экономических моделях |
| В данном примере рассмотрим способы нахождения значений функций в математическом анализе с использованием различных методов, таких как подстановка, арифметические операции и прочие. | Программирование предоставляет возможность использовать функции для автоматизации вычислений. С помощью примеров покажем, как происходит вычисление значений функции в коде на определенном языке программирования. | В экономических моделях функции играют важную роль. Представим практическую задачу и рассмотрим процесс определения значения функции, отражающей экономические зависимости и взаимосвязи. |
Каждый из примеров позволяет наглядно продемонстрировать процесс вычисления значений функциональной зависимости в различных областях знаний и практическом применении. Познакомившись с этими примерами, вы сможете лучше понять принципы и методы вычисления значений функции в разных контекстах.
Важные нюансы при применении алгоритма

Одной из ключевых задач при использовании алгоритма является правильный выбор функциональной зависимости, которая наилучшим образом описывает искомую величину. Важно учитывать возможность нелинейных зависимостей, отклонений и прочих особенностей, которые могут влиять на результат.
Другим важным аспектом является выбор соответствующих методов и алгоритмов для нахождения значения функции. Здесь важно обратить внимание на различные факторы, такие как сложность вычислений, точность результатов, время выполнения и доступность необходимых данных.
Также следует не забывать о валидации и проверке полученных результатов. Это позволяет убедиться в корректности работы алгоритма, а также выявить и исправить возможные ошибки или неточности.
И наконец, важным моментом является правильное документирование и описание примененных методов и алгоритмов. Наличие четкой и понятной документации позволяет другим пользователям алгоритма лучше понять его принципы работы и правильно его применить в своих задачах.
| Важные моменты при использовании алгоритма | Описание |
|---|---|
| Выбор функциональной зависимости | Правильный выбор функциональной зависимости с учетом возможных нелинейных зависимостей и отклонений |
| Выбор методов и алгоритмов | Адекватный выбор методов и алгоритмов в зависимости от требуемой точности, времени выполнения и доступности данных |
| Использование ограничений входных переменных | Учет и ограничение возможных значений входных переменных для избегания некорректных результатов |
| Валидация и проверка результатов | Проверка полученных результатов для выявления и исправления возможных ошибок и неточностей |
| Документирование и описание | Правильное описание и документирование примененных методов и алгоритмов для лучшего понимания другими пользователями |
Преимущества использования данной методики вычисления значений функции
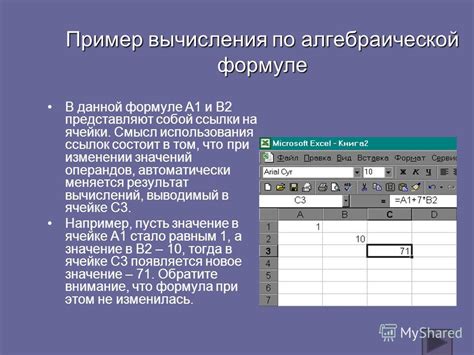
В данном разделе мы рассмотрим преимущества применения данной методики для определения значений функции. Уникальный подход, представленный в этой статье, позволяет достичь результата с помощью простых и легко доступных вычислительных инструментов, не требующих сложных алгоритмов или специальных знаний в математике.
- Эффективность: Применение данного метода позволяет сократить время и затраты на вычисление значений функции. Благодаря простоте и наглядности подхода данный метод может быть использован даже без опыта в программировании или математике.
- Доступность: Не требуя специализированного программного обеспечения или высокой вычислительной мощности, данная методика доступна каждому пользователю. Это делает ее универсальным и удобным инструментом для быстрого определения значений функций в различных ситуациях.
- Надежность: Данный подход использует простые математические операции, что увеличивает надежность и точность результатов. Простота метода позволяет избежать сложных ошибок, связанных с использованием сложных алгоритмов или высокооптимизированных программ.
- Гибкость: Методика позволяет применять ее для разных видов функций, включая как линейные, так и нелинейные. Это дает возможность использовать данный подход в широком спектре задач, связанных с нахождением значений функций, от простых математических задач до более сложных прикладных проблем.
- Обучаемость: Знание данной методики позволяет не только быстро вычислять значения функции, но и обучать других пользователей этому удобному и эффективному подходу. Делись своим опытом с коллегами и друзьями, чтобы они также могли воспользоваться преимуществами этой методики.
Оптимальные рекомендации для эффективного применения алгоритма

В данном разделе представлены ряд практических советов и полезных рекомендаций, которые помогут вам успешно использовать алгоритм для нахождения значений функции. Путем применения следующих стратегий вы сможете повысить эффективность работы алгоритма и достичь более точных результатов.
1. Тщательно выбирайте метод численного решения
Перед началом работы с алгоритмом необходимо выбрать подходящий метод численного решения для вашей конкретной задачи. Изучите различные алгоритмы и их особенности, чтобы определить оптимальный способ нахождения значений функции. Обратите внимание на разницу между методами и их применимостью в вашем конкретном контексте.
2. Оптимизируйте шаги алгоритма
Определите ключевые шаги алгоритма и проанализируйте их в целях оптимизации. Посмотрите, можно ли упростить некоторые операции или сократить количество итераций. Более эффективное использование вычислительных ресурсов поможет существенно ускорить процесс нахождения значений функции.
3. Применяйте подходящую точность вычислений
Определите необходимую точность, с которой требуется вычислить значения функции. Если требуется достичь высокой степени точности, вам придется использовать более сложные методы численного решения и увеличивать количество итераций. Однако, если требуется более грубая оценка значений функции, можно применить более простые и быстрые методы.
4. Проверяйте результаты на различных тестовых данных
Для уверенного применения алгоритма рекомендуется проверить его результаты на различных тестовых данных. Проверьте, как алгоритм работает на разных примерах и в разных условиях. Это поможет вам убедиться в надежности и стабильности решения, а также выявить возможные проблемы и исключить их.
Следуя этим практическим советам и рекомендациям, вы сможете успешно применить алгоритм для нахождения значений функции и достичь более точных и надежных результатов в своих вычислениях.
Вопрос-ответ

В чем заключается данный простой способ нахождения значения функции?
Данный простой способ заключается в подстановке значения аргумента функции в ее аналитическое выражение и последующем вычислении значения функции.
Какой аргумент следует подставлять в функцию для нахождения значения?
Для нахождения значения функции следует подставлять значение аргумента, чей результат интересует. Значение аргумента может быть любым числом, которое является допустимым для данной функции.
Можно ли использовать данный способ для любой функции?
Да, данный способ можно использовать для любой функции, у которой есть аналитическое выражение. Однако, для сложных функций может потребоваться использование математических методов или программ для вычисления значения.



