В мире математики исследование объема куба – это вызов для молодых умов, стремящихся погрузиться в пространство и узнать все его тайны. Это увлекательное исследование, где применяются различные методы и техники для определения этого фундаментального показателя, известного своей важностью и универсальным применением.
А стал ли ты задумываться о том, как этикетки на продуктах, размеры коробок, определенные материалы и габариты родного дома – все это связано с объемом куба? И какой подход позволяет нам увидеть глубину и простор с помощью чисел и формул?
Тогда представь себе, что ты возвращаешься в пятый класс и вновь принимаешься путешествовать по загадочному миру объемов. Забудь на время все понятные тебе определения и вместе с нами открой новые слова и выражения, которые помогут тебе раскрыть тайну объема куба. Давай вместе отправимся в увлекательное путешествие!
Понимание понятия "объем куба"

Объем куба можно описать как меру пространства, занимаемого кубической фигурой. Он является трехмерной характеристикой и позволяет определить, сколько маленьких единичных кубиков может быть размещено внутри данной фигуры.
Размер объема куба зависит от длины его ребра. Чем больше длина ребра, тем больше объем куба, и наоборот. Кроме того, объем куба можно выразить в кубических единицах (например, кубических сантиметрах или кубических метрах).
Для вычисления объема куба можно использовать различные формулы и методы, в зависимости от известных данных. Например, если известна длина ребра куба, то его объем можно вычислить по формуле объем = (длина ребра)^3.
Понимание понятия "объем куба" имеет важное значение не только в геометрии, но и во многих других областях, таких как архитектура, строительство, механика и другие. Это понятие помогает нам анализировать и описывать трехмерные объекты и их взаимодействие.
Связь между ребром куба и его объемом
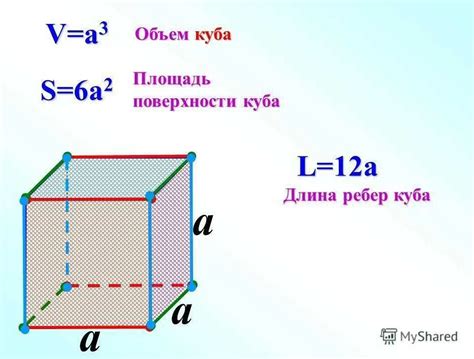
В данном разделе мы рассмотрим важную связь между ребром куба и его объемом. Иными словами, мы узнаем, как изменение длины ребра куба влияет на его объем.
Объем куба представляет собой количество пространства, которое он занимает. Он зависит от трех измерений: длины, ширины и высоты, применяемых к ребру куба. Наша задача состоит в том, чтобы понять, как изменение длины ребра влияет на объем куба.
Известно, что объем куба вычисляется по формуле: объем = длина ребра * длина ребра * длина ребра, или V = a * a * a, где V - объем куба, а a - длина ребра.
Теперь представьте себе, что мы увеличиваем длину ребра куба в 2 раза. Что произойдет с его объемом? Воспользуемся формулой и подставим новое значение длины ребра: V = (2a) * (2a) * (2a) = 2 * 2 * 2 * (a * a * a) = 8 * (a * a * a).
Из данного примера видно, что при увеличении длины ребра в 2 раза, объем куба увеличивается в 8 раз. Это означает, что связь между длиной ребра и объемом куба является кубической, поскольку изменение длины ребра влияет на объем в кубической степени.
Описание метода определения объема куба при известной длине ребра

В данном разделе рассмотрим метод, позволяющий определить объем куба, когда известна длина его ребра. На основе данного метода можно точно вычислить объем куба без необходимости измерения дополнительных параметров.
Прежде чем перейти к описанию метода, рассмотрим определение ключевых понятий. Куб - это особый вид геометрического тела, обладающий свойствами симметрии и правильности формы. Ребро куба - это одна из шести равных, параллельных граней, составляющих его структуру.
Таким образом, для нахождения объема куба при известной длине его ребра, необходимо применить следующий метод:
- Измеряем длину ребра куба с помощью линейки или мерной ленты.
- Возводим значение длины ребра в куб (умножаем его само на себя) для получения объема куба.
- Полученный результат является объемом куба и выражается в кубических единицах измерения (например, кубические сантиметры, кубические метры).
Таким образом, мы можем определить объем куба при известной длине его ребра, используя вышеописанный метод без необходимости измерения других параметров.
Расчет объема куба через возведение в куб
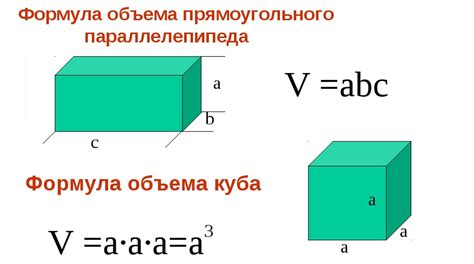
Примеры задач по вычислению размера граней квадрата

В данном разделе представлены различные примеры задач, которые помогут разобраться в расчете размера граней квадрата без использования специфических определений из математического курса 5 класса.
- Задача 1: Найдите объем куба, если известно, что его длина стороны равна 5 метрам.
- Задача 2: Определите длину стороны куба, если его объем составляет 27 кубических метров.
- Задача 3: Рассчитайте объем куба, если известно, что его площадь грани равна 36 квадратных сантиметров.
- Задача 4: Найдите площадь грани куба, если его объем равен 125 кубическим сантиметрам.
- Задача 5: Определите объем куба, зная длину ребра грани, равную 8 миллиметрам.
Решение данных задач поможет понять основные понятия связанные с расчетом объема куба и позволит применить полученные знания в практических ситуациях.
Описание способа нахождения длины стороны куба при известном объеме
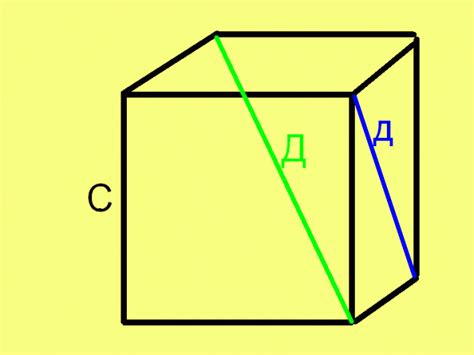
Рассмотрим один из методов определения длины стороны куба, когда известен его объем. Данная процедура позволяет найти необходимое значение при помощи определенных математических операций.
- Найдите кубический корень из известного объема куба. Полученное значение будет представлять длину стороны, так как кубический корень показывает, с каким числом нужно умножить само себя два раза, чтобы получить исходное число.
- Для этого используйте специальные математические операции, такие как кубирование или возведение в третью степень.
- Полученное значение станет искомой стороной куба, при условии, что известен только его объем. Этот метод позволяет определить длину стороны без прямого знания других характеристик куба.
Таким образом, при известном объеме куба возможно определить длину его ребра, используя кубический корень и математические операции, такие как кубирование или возведение чисел в степень. Этот способ позволяет решить задачу без необходимости знания других характеристик куба в 5 классе.
Практические примеры определения ребра куба
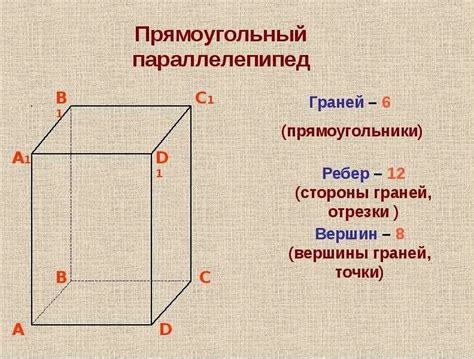
В этом разделе мы рассмотрим некоторые практические примеры, которые помогут нам определить длину ребра куба. Мы избегаем использования конкретных определений, а вместо этого предлагаем рассмотреть методы, с помощью которых можно узнать размер сторон куба.
Первый пример связан с измерением объема жидкости, которую можно налить в кубический контейнер. Зная, что объем куба определяется как произведение длины, ширины и высоты, мы можем, например, заполнить кубическую коробку водой и затем измерить, сколько литров жидкости в неё влезет. После этого, зная значения ширины и высоты, можно поделить объем на произведение этих двух значений, чтобы получить длину ребра куба.
Второй пример связан с использованием геометрической фигуры, схожей с кубом, такой как правильный параллелепипед. Такой параллелепипед имеет три равные стороны, что позволяет нам использовать его для определения ребра куба. Мы можем измерить длину одной из сторон параллелепипеда и затем использовать это значение для определения ребра куба.
Третий пример связан с использованием предметов, которые обладают формой, близкой к кубу. Например, мы можем использовать столешницу кубической формы или кубическую коробку с вещами внутри. Мы хорошо знаем размеры этих предметов и можем использовать их для определения ребра куба.
Задачи для самостоятельного решения по объему кубика

В данном разделе представлены задачи, которые помогут учащимся 5 класса самостоятельно закрепить материал по вычислению объема куба. Задачи разной сложности поэтапно вводят детей в мир геометрии, развивая их логическое мышление и способности к решению простых задач.
- Антон построил куб с ребром 3 см. Каков его объем?
- В комнате, имеющей форму куба, находится книжная полка. Ее размеры также являются ребрами куба. Если ребро книжной полки равно 2 метра, то каков объем книжной полки?
- Катя стала строить песочные кубики на пляже. Она сделала первый куб со стороной 10 см. Следующие кубики она делала в два раза меньше предыдущего. Какой объем у последнего кубика, если Катя построила 5 кубиков?
- Ребята на уроке изобразили на асфальте куб со стороной 50 см. Каков объем воздуха, ограниченный данной фигурой?
- У детей имеются одинаковые деревянные кубики, из которых можно сложить куб со стороной 15 см. Каков будет объем такого куба?
Решите данные задачи самостоятельно. При необходимости используйте полученные ранее знания о величине объема куба и примените соответствующие способы вычисления. Проверьте свои ответы по окончании задач и постарайтесь найти различные подходы к их решению.
Игра "Отыщи содержание квадра" для закрепления знаний

В этом разделе мы предлагаем вам игровую активность, которая поможет закрепить изученный материал о характеристиках куба. В игре "Найди объем куба" вы сможете проверить свои знания и навыки, используя веселую и увлекательную форму обучения.
Вам потребуется набор карточек с различными изображениями кубов. Каждая карточка имеет специальные маркеры, обозначающие стороны куба - длину, ширину и высоту. Ваша задача состоит в том, чтобы находить карточки с одинаковыми объемами кубов и объединять их в пары.
- Начните игру, смешав все карточки и разложив их на столе.
- Выберите первую карточку и обратите внимание на ее маркеры.
- Продолжайте искать другие карточки с теми же маркерами, чтобы найти пары.
- Когда вы нашли пару, положите обе карточки рядом и продолжайте с следующей.
- Игра продолжается до тех пор, пока все карточки не будут объединены в пары.
Игра "Найди объем куба" поможет вам визуализировать и запомнить, какие характеристики кубов определяют их объемы. Кроме того, она развивает логическое мышление, внимательность и способность находить соответствия.
Вопрос-ответ

Какими способами можно определить объем куба в 5 классе?
В 5 классе для определения объема куба можно использовать несколько способов. Один из них - это формула для вычисления объема куба, которая звучит как V = a^3, где "V" - объем, а "a" - длина ребра куба. Другой способ - это построение модели куба из кубиков или использование математических наборов для измерения объема.
Какие инструменты можно использовать для определения объема куба в 5 классе?
Для определения объема куба в 5 классе можно использовать несколько инструментов. Во-первых, это линейка или метрологическая лента, чтобы измерить длину ребра куба. Во-вторых, можно воспользоваться геометрическими моделями кубов или материалами для конструирования, чтобы визуально представить пространство куба и его объем. Кроме того, дополнительно могут быть использованы компьютерные программы или приложения для расчета объема куба.



