Глубоко в самых недрах научных исследований притаилась одна из величайших тайн физики - схема, способная открывать для нас необыкновенные экстремумы возможностей. Вслед за началом увлекательного путешествия по миру наук, мы шагнем вместе с вами в грандиозный мир неизведанных граней физической реальности. Откройте своему взору непроглядные покровы невидимых физических законов, которые столь ужасно и восхитительно влияют на наше существование.
Схема, которая обещает наши сознания замутить, позволяет брать и развивать на подступах к пикам нашего потенциала - это ключ, открыющий створки безграничных возможностей. Только самые отважные и настойчивые вознаграждаются революционными открытиями и обретают возможность заглянуть за горизонт привычного сознания. Никто не может предсказать, к каким дивным мирам ведет путешествие в поисках экстремумов. Нелясь в приключениях научных открытий, мы начинаем понимать, что наши границы находятся где-то далеко за гранью представимого.
Колоссальное удовлетворение пленительно обретаем в результате постижения новых знаний и расширения взглядов на окружающий мир. Однако этот путь исполнен опасностей и страстей, как путешествие по морской глубине. Тем, кто не готов рисковать и не верит в свои силы, остается лишь смотреть на замкнутые двери непознанного. Но мы смело захлопнем их, бросим вызов монотонности нашего существования и вместе восхитимся новыми гранями возможностей. Данный раздел представляет собой последовательность изумительных доводов и необычных фактов, которые заставят вас обратиться к тайнам экстремальных сфер физической реальности.
Понятие "экстремума возможности": определение и связь с физикой

Термин "экстремум" означает точку, в которой достигается минимум или максимум функции или значения показателя. В контексте физики, экстремумы возможности могут представлять собой, например, максимально возможную энергию, оптимальные параметры системы, наибольшую скорость или наименьшую дисперсию.
Определение и изучение экстремумов возможности в физике имеет важное значение для понимания и прогнозирования поведения физических систем. Это позволяет оптимизировать работу системы, выбрать наилучшие параметры и достичь максимальных результатов.
Для анализа и поиска экстремумов возможности в физике применяются различные методы и подходы, включая использование математических моделей, оптимизационных алгоритмов и экспериментальных исследований. Этот процесс требует глубокого понимания физических принципов и законов, а также навыков математического моделирования и анализа данных.
Изучение экстремумов возможности в физике позволяет не только определять оптимальные условия и параметры системы, но и находить новые закономерности и явления, которые могут быть использованы в различных областях науки и техники. Таким образом, понятие "экстремума возможности" играет важную роль в понимании и развитии физической науки.
Принципы исследования предельных значений в физических системах

| Принцип | Описание |
|---|---|
| Принцип экстремума энергии | Система будет стремиться к минимизации своей энергии или максимизации ее отдачи. Изменение параметров системы может привести к изменению ее энергетического состояния и, следовательно, достижению новых экстремальных значений. |
| Принцип максимума энтропии | Система будет стремиться к наиболее вероятному распределению своих частиц, при котором энтропия системы будет максимальной. Изменение условий или параметров системы может привести к изменению ее энтропийного состояния и, соответственно, достижению новых экстремумов возможности. |
| Принцип наибольшего или наименьшего действия | В пространстве всех возможных траекторий системы она будет двигаться по пути наименьшего или наивысшего действия. Соответствующий принцип действия представляет собой функционал, зависящий от параметров системы, и его вариации позволяют определить экстремальные значения. |
Данные принципы являются основой для анализа и прогнозирования поведения физических систем. Их использование позволяет установить оптимальные условия, при которых система может демонстрировать максимальную эффективность и стабильность, а также обнаружить возможные экстремальные состояния, которые могут проявиться в системе при изменении параметров.
Математические методы для выявления экстремальных значений возможностей в науке о природе

Одним из ключевых математических инструментов, используемых для поиска экстремумов возможностей, является метод дифференциального исчисления. Он позволяет находить точки экстремума путем анализа производных функций, что позволяет исследователям определить, где находятся локальные максимумы и минимумы.
Для более сложных и многомерных задач поиска экстремумов возможностей в физике применяются методы матричной алгебры. Они позволяют исследователям анализировать системы уравнений и находить их экстремальные значения с помощью операций с матрицами и векторами.
Еще одним из используемых методов для поиска экстремумов возможностей в физике является метод наименьших квадратов. Он используется для аппроксимации данных и нахождения наилучшей прямой или кривой, которая подходит к имеющимся данным с минимальной ошибкой. Этот метод позволяет исследователям находить экстремальные значения параметров моделей, основываясь на экспериментальных данных.
- Метод дифференциального исчисления
- Методы матричной алгебры
- Метод наименьших квадратов
Применение аналитического подхода к изучению крайних значений потенциала в научных исследованиях
Для достижения оптимальных результатов и глубокого понимания физических явлений и процессов в науке, применяется аналитический подход к изучению экстремальных значений возможности. Аналитический подход позволяет систематически анализировать данные и определять оптимальные точки или максимумы и минимумы в физических системах.
В контексте исследования аналитического подхода к поиску экстремальных значений потенциала в физике, аналитики обнаруживают и понимают точки, в которых физическая система достигает наибольших или наименьших возможностей. Применение аналитического подхода позволяет исследователям определить критические точки, где физическая система переходит из одного состояния в другое и происходят важные физические явления. Основываясь на полученных результатах, ученые могут разрабатывать новые теории и модели, которые помогут объяснить и предсказать поведение системы.
- Аналитический подход в физике позволяет подробно исследовать процессы, происходящие в физической системе.
- Аналитический подход помогает выявить критические точки и определить оптимальные значения физических параметров.
- Использование аналитического подхода позволяет ученым создавать новые теории и модели для объяснения и предсказания поведения системы.
- Аналитический подход является важным инструментом в научных исследованиях и помогает расширить наше понимание физических процессов.
Результаты аналитического подхода могут быть применены в различных областях физики, таких как теоретическая физика, квантовая механика, статистическая физика и другие. Применение аналитического подхода к поиску экстремальных значений потенциала позволяет ученым углубляться в изучение фундаментальных законов и принципов физической реальности и создавать новые возможности для развития науки.
Применение численных алгоритмов для определения крайних значений возможностей в научных исследованиях

Для достижения наиболее точных результатов в физических исследованиях необходимо обнаружить экстремумы возможностей, которые могут быть достигнуты в данной системе. Однако, поскольку предмет исследования обычно сложен и многофакторен, традиционные методы поиска могут быть недостаточно эффективными.
В этом разделе рассматривается применение численных методов для поиска экстремумов возможностей в физике. Численные алгоритмы позволяют учеть множество факторов и проводить более точные расчеты, не ограничиваясь аналитическими решениями.
Одним из таких численных методов является метод оптимизации, который позволяет находить экстремумы целевой функции путем пошаговой минимизации или максимизации. Этот метод основан на прогнозировании оптимальных значений параметров системы и проведении нескольких итераций для приближения к глобальному экстремуму.
Кроме того, в современных исследованиях активно применяются методы многокритериальной оптимизации, которые позволяют учитывать несколько целевых функций одновременно. Это особенно важно, когда требуется достичь компромисса между несколькими параметрами или приоритетами.
Преимущества использования численных методов для поиска экстремумов возможностей в физике очевидны: повышенная точность, эффективность и учет множества факторов. Эти методы позволяют исследователям систематически исследовать все возможные варианты и выбрать оптимальные решения для своих целей.
Экспериментальный подход к поиску предельных точек достижимых значений

Обоснованное исследование возможностей в физике требует не только аналитических методов, но и экспериментального подтверждения. Экспериментальный подход к поиску предельных точек достижимых значений позволяет проверить и обнаружить такие особые состояния системы, которые могут быть недоступны аналитическим аппаратом. Это подход активно применяется в различных областях физики, где синтез опытных данных и теоретических моделей позволяет получить более полное представление об экстремальных явлениях.
В экспериментальном подходе к поиску предельных точек достижимых значений используются различные методы измерений и экспериментов, позволяющие контролировать и варьировать параметры системы. Это может быть изменение внешних условий, применение специальных техник измерений или использование специализированных устройств для регистрации и анализа данных. Основным преимуществом экспериментального подхода является возможность получения реальных результатов, которые могут быть сопоставлены с результатами теоретических расчетов.
Важной составляющей экспериментального подхода является учет неопределенностей и погрешностей измерений. При анализе экспериментальных данных необходимо учитывать статистические и систематические погрешности, а также принимать во внимание неоднородность системы и возможные внешние воздействия. Это позволяет получить более достоверные результаты и оценить предельные точки достижимых значений с учетом всех возможных факторов.
Роль анализа локальных максимумов и минимумов в различных сферах физического познания
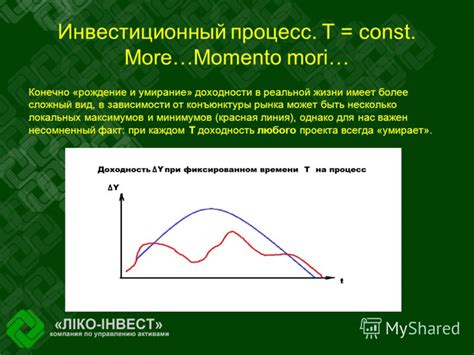
В данном разделе мы рассмотрим значимость исследования локальных экстремальных точек в различных областях физики. Это аналитический метод, позволяющий определить важные состояния и процессы в природе, используя максимумы и минимумы функционалов. Такой подход позволяет уловить важные закономерности и инсайты, критические для понимания физических явлений.
Начнем с области математической физики, где изучение локальных экстремальных точек функций является неотъемлемой частью анализа сложных систем. Основываясь на определении критических значений, мы можем определить стационарные состояния и точки перехода, играющие решающую роль в теориях электромагнетизма, квантовой механики и термодинамики.
Переходя к области астрофизики, изучение локальных экстремумов возможности позволяет анализировать процессы внутри звезд, галактик и космических объектов. Экстремальные точки дают информацию о стадиях развития звездных систем, действии гравитационных сил и магнитных полей, а также о формировании черных дыр и других астрономических объектов.
Далее, в области квантовой физики, локальные экстремумы возможности играют фундаментальную роль в определении структуры и свойств элементарных частиц. Используя методы поиска максимумов и минимумов, физики могут находить важные частицы, описывающие сложные явления в элементарной физике и строить модели, прогнозирующие новые явления.
Наконец, в области физиологии и медицины, локальные экстремумы возможности используются для изучения электрической активности мозга и других биологических систем. Здесь анализ экстремальных точек позволяет выявить взаимосвязи между различными электрическими сигналами, например, для определения функциональных областей мозга или диагностики патологических состояний.
- Рассмотрели роль исследования локальных максимумов и минимумов в разных областях физики;
- Показали применимость данных методов в математической физике, астрофизике, квантовой физике и медицине;
- Обозначили ключевые результаты, которые можно получить при анализе локальных экстремальных точек;
- Подчеркнули важность этих методов для понимания физических явлений и развития науки в целом.
Применение схемы поиска точек экстремума в реальных задачах

В данном разделе рассматриваются конкретные примеры использования схемы, позволяющей находить точки максимума или минимума различных показателей в различных областях науки.
Прежде всего, применение данной схемы находит широкое применение в исследованиях, связанных с оптимизацией различных процессов. Например, в инженерных решениях, где требуется найти оптимальные параметры для достижения наилучшей производительности системы или максимизации прибыли.
- В экономике это может быть оптимальное распределение ресурсов для максимизации прибыли или минимизации затрат.
- В биологии схема может использоваться для определения оптимальных условий развития организма или поиска максимальной эффективности действия лекарственных препаратов.
- В физиологии это может быть поиск оптимальных показателей для достижения наилучшей физической формы или поиска режимов тренировок, при которых вырабатывается максимум энергии.
Схема поиска экстремумов возможности также применяется в прикладной математике и физике. Например, в задачах оптимального управления или оптимального проектирования, где требуется найти наилучшие значения параметров для достижения желаемого результата.
Во всех этих примерах схема поиска точек экстремума позволяет эффективно оптимизировать рассматриваемые процессы и достичь наилучших результатов в заданных условиях.
Вопрос-ответ

Какие методы используются в схеме поиска экстремумов возможности в физике?
В схеме поиска экстремумов возможности в физике используются различные методы, такие как метод наименьших квадратов, метод градиентного спуска, метод Ньютона и другие. Эти методы позволяют находить экстремумы функций, оптимальные значения параметров и другие интересные точки.
Какая роль схемы поиска экстремумов возможности в физике?
Схема поиска экстремумов возможности в физике играет важную роль в оптимизации и анализе систем. Она позволяет находить оптимальные значения параметров, минимумы и максимумы функций, точки, в которых находятся экстремумы возможности. Это позволяет исследовать системы, оптимизировать их работу и принимать более эффективные решения.
Как применяется схема поиска экстремумов возможности в физике в реальной жизни?
Схема поиска экстремумов возможности в физике применяется во многих областях реальной жизни. Например, она используется в физическом моделировании и оптимизации процессов. Также с ее помощью можно исследовать и оптимизировать работу различных систем, например, проектировать лучшие алгоритмы управления, оптимизировать трафик на дорогах, настраивать параметры работы энергетических установок и многое другое.



