Когда речь заходит о прогнозировании значений переменных, линейная регрессия является одним из наиболее часто используемых и эффективных методов в машинном обучении. Она позволяет установить взаимосвязь между зависимой переменной и одной или несколькими независимыми переменными, основываясь на простой линейной функции.
В основе принципа работы линейной регрессии лежит предположение, что зависимая переменная может быть предсказана с помощью линейной комбинации независимых переменных. Данное предположение выражается в виде математической модели, которая представляет собой уравнение прямой линии, описывающей предсказываемую величину.
Основная задача линейной регрессии состоит в том, чтобы найти оптимальные значения коэффициентов уравнения прямой линии, чтобы минимизировать ошибку предсказания. Для этого используется метод наименьших квадратов, который подбирает такие коэффициенты, чтобы сумма квадратов отклонений между фактическими и предсказанными значениями была минимальной.
Значение линейной регрессии в машинном обучении

Линейная регрессия основана на идее поиска линейной зависимости между независимыми и зависимой переменными. Она позволяет находить оптимальные коэффициенты, с помощью которых можно приблизить исходные данные к линейной модели. Такая модель может быть использована для прогнозирования и анализа данных, а также для понимания связи между различными переменными.
Применение линейной регрессии в машинном обучении особенно полезно в ситуациях, когда мы имеем большую выборку данных и хотим построить модель, которая может прогнозировать значения на основе этих данных. Она может быть использована для анализа роста, спроса на товары или услуги, прогнозирования будущих тенденций и многое другое.
Существуют различные типы линейной регрессии, которые могут быть применены в зависимости от типа данных и требуемых результатов. Некоторые из них включают простую линейную регрессию, множественную линейную регрессию, полиномиальную регрессию и регрессию с регуляризацией.
- Простая линейная регрессия позволяет прогнозировать значения одной переменной на основе одной независимой переменной.
- Множественная линейная регрессия позволяет прогнозировать значения одной переменной на основе нескольких независимых переменных.
- Полиномиальная регрессия позволяет прогнозировать значения переменной на основе полиномиальной функции.
- Регрессия с регуляризацией позволяет учитывать штрафы за сложность модели и способствует борьбе с переобучением.
Роль линейной регрессии в машинном обучении состоит в том, чтобы помочь анализировать данные, строить модели и предсказывать значения на основе этих моделей. Она широко используется в различных областях, таких как экономика, финансы, маркетинг и другие, и является одним из фундаментальных инструментов машинного обучения.
Основы построения модели линейной зависимости

В процессе построения модели линейной регрессии, основная задача заключается в определении оптимальных значений коэффициентов, которые будут наилучшим образом описывать взаимосвязь между независимыми переменными и зависимой переменной. Для этого используется метод наименьших квадратов, который позволяет минимизировать сумму квадратов разностей между фактическими и предсказанными значениями.
Ключевой идеей линейной регрессии является представление зависимой переменной как комбинации линейных вкладов независимых переменных, взятых с определенными весами (коэффициентами). Таким образом, модель линейной регрессии строится на основе предположения о линейной связи между переменными и позволяет оценить влияние каждой независимой переменной на зависимую переменную.
Идея моделирования зависимости с помощью прямой линии

Главная задача линейной регрессии заключается в нахождении такого уравнения прямой линии, которое наилучшим образом приближает наблюдаемые данные. Прямая линия может быть описана уравнением вида y = mx + b, где x - независимая переменная, y - зависимая переменная, m - угловой коэффициент (наклон прямой) и b - свободный член (точка пересечения с осью y).
| Пример данных | Уравнение прямой линии | ||
|---|---|---|---|
| x | y | ||
| 1 | 3 | y = 2x + 1 | |
| 2 | 5 | ||
| 3 | 7 | ||
| 4 | 9 | ||
| 5 | 11 |
В таблице представлен пример данных, где значения зависимой переменной y изменяются в соответствии с независимой переменной x. Если построить эти значения на графике, то можно заметить, что они лежат на одной прямой линии. Задача линейной регрессии состоит в том, чтобы найти уравнение этой прямой таким образом, чтобы сумма расстояний между наблюдаемыми значениями и предсказанными значениями была минимальной.
Метод наименьших квадратов является одним из распространенных подходов к нахождению уравнения прямой линии. Он минимизирует сумму квадратов отклонений предсказанных значений от фактических значений. Используя этот метод, линейная регрессия находит оптимальные значения углового коэффициента и свободного члена для линии, которая наилучшим образом подходит к наблюдаемым данным.
Выбор целевой переменной

Для определения целевой переменной необходимо ясно сформулировать цель и задачи модели. Целевая переменная должна быть тесно связана с поставленными задачами и отображать интересующий аспект данных. Часто целевая переменная представляет собой величину, которую необходимо предсказать, как, например, стоимость недвижимости, число продаж товара или уровень дохода.
При выборе целевой переменной необходимо также учитывать ее доступность и качество. Исходя из имеющихся данных, целевая переменная должна быть измерима и иметь достаточное количество значений. Большое количество пропущенных значений или недостаточная вариативность могут сильно сказаться на качестве модели.
Еще одним важным фактором при выборе целевой переменной является ее интерпретируемость. Целевая переменная должна быть понятной и иметь смысл для конечных пользователей модели. Это позволит лучше понимать предсказанные результаты и принимать обоснованные решения на основе модели.
В целом, выбор целевой переменной требует внимательного анализа и учета различных факторов, чтобы достичь точности и релевантности предсказаний модели.
Отбор признаков для модели

Отбор признаков является процессом идентификации наиболее релевантных и значимых переменных из множества доступных признаков. Это позволяет улучшить понимание взаимосвязей между признаками и целевой переменной, а также снизить размерность пространства признаков и избавиться от лишней информации.
Существует несколько подходов к отбору признаков. Один из них - это статистический анализ, основанный на оценке степени корреляции между каждым признаком и целевой переменной. Анализ важности признаков может основываться на различных статистических показателях, таких как коэффициент корреляции Пирсона или взаимная информация.
Ещё один подход к отбору признаков - это использование алгоритмов машинного обучения, способных сами определить важность каждого признака для модели. Некоторые алгоритмы, такие как случайный лес или градиентный бустинг, предоставляют встроенные методы выбора признаков, основанные на анализе их вклада в принятие решений.
Метод наименьших квадратов

В данном разделе рассмотрим основной метод, который используется в линейной регрессии для построения модели зависимости между независимой и зависимой переменными. Этот метод, известный как метод наименьших квадратов, позволяет нам найти линейную функцию, которая наилучшим образом приближает исходные данные. Он основывается на принципе минимизации суммы квадратов разностей между значениями модели и фактическими значениями целевой переменной.
Суть метода наименьших квадратов заключается в поиске таких коэффициентов линейной функции, чтобы сумма квадратов ошибок была минимальной. Это позволяет нам получить наилучшую аппроксимацию данных и, следовательно, предсказывать значения зависимой переменной на основе известных независимых переменных. Для решения этой задачи используется система уравнений, которая позволяет найти оптимальные значения коэффициентов.
Для применения метода наименьших квадратов необходимо выполнить следующие шаги:
- Собрать данные по исследуемой проблеме, включая значения зависимой переменной и соответствующие значения независимых переменных.
- Выбрать линейную модель, которая наилучшим образом представляет связь между переменными.
- Решить систему уравнений с помощью метода наименьших квадратов, чтобы определить оптимальные значения коэффициентов.
- Получить уравнение линейной регрессии с найденными коэффициентами.
- Проверить качество модели на основе метрик, таких как коэффициент детерминации и средняя ошибка модели.
Метод наименьших квадратов является фундаментальным инструментом для обучения моделей линейной регрессии в машинном обучении. Он позволяет находить оптимальные параметры модели, которые максимально приближают реальные данные и позволяют делать предсказания с минимальной ошибкой.
| Преимущества | Недостатки |
|---|---|
| Простота реализации | Чувствительность к выбросам |
| Интерпретируемость результатов | Подверженность мультиколлинеарности |
| Вычислительная эффективность |
Применение линейной регрессии для прогнозирования

Основная идея линейной регрессии заключается в поиске оптимальной прямой линии (или гиперплоскости в многомерном случае), которая наилучшим образом соответствует имеющимся данным. При прогнозировании линейная регрессия анализирует зависимость между зависимой переменной и одним или несколькими предикторами, определяет их взаимосвязь и на основе этой информации строит модель для предсказания будущих значений.
Прогнозирование с использованием линейной регрессии может выполняться как для числовых данных, так и для категориальных. Например, в экономике линейная регрессия может применяться для прогнозирования стоимости товаров на основе различных факторов, таких как инфляция, курс валюты, уровень безработицы и т.д. В медицине она может использоваться для прогнозирования длительности выживания пациента на основе возраста, пола и диагноза.
Применение линейной регрессии для прогнозирования требует не только математической модели, но и предварительного анализа и обработки данных. Основные шаги в процессе прогнозирования включают выбор подходящих предикторов, оценку значимости их влияния на зависимую переменную, подготовку тренировочного и тестового наборов данных, обучение модели, оценку ее точности и, наконец, использование модели для прогнозирования новых значений.
Оценка достоверности модели
Для эффективной работы модели линейной регрессии важно обеспечить как можно более точное предсказание значений целевой переменной. Однако, не всегда модель сразу дает идеальные результаты, поэтому важно иметь возможность оценить достоверность ее предсказаний.
Оценка точности модели является важным этапом в процессе анализа данных и является показателем того, насколько хорошо модель соответствует реальным данным. Чтобы оценить точность модели, мы можем использовать различные метрики, такие как средняя абсолютная ошибка (MAE), средняя квадратичная ошибка (MSE), корень из среднеквадратичной ошибки (RMSE) и др.
В процессе оценки точности модели, также можно использовать методы кросс-валидации, которые позволяют более объективно оценить качество модели и избежать переобучения. Кросс-валидация заключается в разделении исходного набора данных на обучающую и тестовую выборки, после чего модель обучается на обучающей выборке и проверяется на тестовой.
Оценка точности модели является важным инструментом, который позволяет определить, насколько хорошо модель обучается на данных и способна предсказывать значения целевой переменной. Чем выше точность модели, тем более достоверные результаты она будет давать при решении задачи прогнозирования.
Анализ результатов линейной модели: понимание взаимосвязей
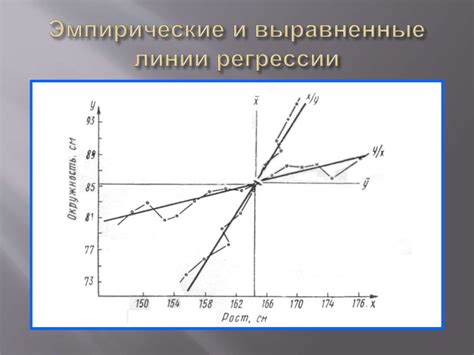
После получения результатов линейной регрессии, необходимо проанализировать и интерпретировать полученные значения. Основная идея данного раздела заключается в понимании взаимосвязей между признаками и целевой переменной на основе коэффициентов, статистик и интервалов значений.
Для начала, следует проанализировать значимость коэффициентов линейной модели. Коэффициенты позволяют определить, как каждый признак влияет на целевую переменную. Интерпретация положительного или отрицательного знака коэффициента может указывать на направление и силу связи между признаком и целевой переменной.
Дополнительно, полезной информацией являются статистические метрики, такие как коэффициент детерминации (R-квадрат), который позволяет оценить объясняющую способность модели. Значение R-квадрат близкое к единице указывает на высокую объясняющую способность модели в отношении целевой переменной, в то время как значения близкие к нулю говорят о низкой эффективности модели.
Также необходимо рассмотреть значимость статистических тестов для оценки гипотезы о значимости коэффициентов. Если p-значения меньше установленного уровня значимости, то можно утверждать, что признак является статистически значимым для модели.
Интерпретация результатов линейной регрессии требует также учета интервалов значений коэффициентов. Интервалы с большой шириной указывают на более неопределенные оценки, в то время как узкие интервалы свидетельствуют о высокой уверенности в значениях коэффициентов.
В итоге, анализ результатов линейной регрессии позволяет понять, какие признаки оказывают наибольшее влияние на целевую переменную, оценить объясняющую способность модели, определить степень значимости признаков и оценить уверенность в значениях коэффициентов.
Вопрос-ответ

Как работает линейная регрессия в машинном обучении?
Линейная регрессия - это алгоритм машинного обучения, который позволяет установить линейную зависимость между одной зависимой переменной и одной или несколькими независимыми переменными. Алгоритм определяет линию наилучшего соответствия между данными, чтобы предсказывать значения зависимой переменной на основе независимых переменных.
Какие принципы лежат в основе работы линейной регрессии?
Основным принципом работы линейной регрессии является минимизация суммы квадратов разностей между реальными значениями зависимой переменной и предсказанными значениями. Для этого алгоритм использует метод наименьших квадратов, который находит оптимальные коэффициенты линейной функции, чтобы минимизировать ошибку предсказания.
Какие данные могут быть использованы для применения линейной регрессии?
Для применения линейной регрессии необходимы данные, которые содержат зависимую переменную и одну или несколько независимых переменных. Зависимая переменная должна быть количественной, тогда как независимые переменные могут быть как количественными, так и категориальными.
Как оценить качество предсказаний в линейной регрессии?
Оценка качества предсказаний в линейной регрессии может осуществляться с помощью различных метрик, таких как среднеквадратичное отклонение (Mean Squared Error, MSE), средняя абсолютная ошибка (Mean Absolute Error, MAE), коэффициент детерминации (R-squared) и другие. Метрики позволяют оценить точность предсказаний и понять, насколько модель хорошо соответствует данным.
Можно ли применить линейную регрессию, если данные имеют нелинейные зависимости?
Линейная регрессия предназначена для моделирования линейных зависимостей, поэтому если данные имеют нелинейные зависимости, применение линейной регрессии может быть недостаточным. В таких случаях можно использовать методы преобразования данных или рассмотреть другие алгоритмы машинного обучения, способные моделировать нелинейные зависимости, например, полиномиальную регрессию или методы основанные на ансамблях моделей.



