Давайте сделаем небольшой эксперимент: представьте себя в мире, где числа и строки, буквы и знаки, создают огромное пиршество математической гимнастики, в которой каждое действие наполнено красотой и грацией. А сегодня мы вместе отправимся в одно из самых интересных и захватывающих мест - мир дробей! Пускай наш ум встретит испытание, а наше воображение освободится и взлетит в неизведанные высоты.
Дроби, эти таинственные символы, покажут нам свои секреты. И вместе мы научимся ореолировать их волшебством и изображать их с помощью скобок. Скобки - это наши рабочие инструменты, которые помогут нам соединить числа и частицы в одно целое, добавить яркие краски и выразить наши мысли с большей точностью. Дроби со скобками - это, пожалуй, один из самых элегантных и эффективных способов представления числовых отношений.
Мы начнем с простого, расширяя свой кругозор постепенно. Скобки сами по себе являются мощным инструментом в математике, и мы научимся применять их в создании дробей. Здесь нас ждет увлекательное путешествие, которое поможет нам перепрыгнуть через рамки обычных представлений и открыть новые горизонты знаний.
Роль скобок в работе с дробями: почему они важны
Скобки могут быть использованы для группировки числителя и знаменателя дробей, а также для выделения и приоритезации операций. Посредством скобок можно явно указать, что операции внутри скобок должны быть выполнены раньше, чем операции снаружи. Это помогает избежать ошибок и повышает точность вычислений.
Кроме того, скобки позволяют создавать сложные выражения, включающие несколько операций с дробями. Они позволяют упростить и структурировать выражения, облегчая понимание и чтение математических задач.
- Скобки можно использовать для задания приоритета операций
- Они обеспечивают понимание и правильное выражение математических операций
- Скобки позволяют группировать числитель и знаменатель дробей
- Они упрощают чтение и понимание сложных выражений с дробями
Основные понятия
В данном разделе будут рассмотрены основные концепции, которые помогут разобраться в теме дробей с использованием скобок. Здесь мы приведем ключевые термины и определения, которые помогут вам лучше понять и применять эти понятия в практике.
- Дробь - это числовое выражение, состоящее из числителя и знаменателя, разделенных чертой.
- Числитель - числовое значение дроби, расположенное над чертой.
- Знаменатель - числовое значение дроби, расположенное под чертой.
- Сокращение дроби - процесс упрощения дроби путем деления числителя и знаменателя на их общий делитель.
- Простая дробь - дробь, в которой числитель меньше знаменателя.
- Смешанная дробь - дробь, состоящая из целой части и обыкновенной дроби.
- Периодическая десятичная дробь - десятичная запись дроби, в которой одна или несколько цифр повторяются бесконечно.
Понимание этих ключевых понятий позволит вам легче освоить и применять техники работы с дробями, в том числе с использованием скобок. Теперь, когда мы уточнили основные определения, перейдем к более конкретным аспектам изучения дробей и использованию скобок в 5 классе.
Что означают числитель и знаменатель дроби?

В учении о дробях важной ролью играют такие понятия, как числитель и знаменатель. Они помогают нам понять, какую долю целого представляет дробь и какую роль играют числа в ее записи.
Числитель – это верхняя часть дроби, которая указывает, сколько частей из целого мы рассматриваем. Грубо говоря, это количество долей, которое у нас есть или которые мы выбираем из целого.
Знаменатель – это нижняя часть дроби, которая определяет, на сколько равных частей поделено целое. Все эти части по своей величине равны и образуют единицу. Знаменатель, по сути, указывает на количество равных долей, на которые делится целое и обычно обозначается цифрой.
Чтобы лучше понять разницу между числителем и знаменателем, рассмотрим пример: дробь 3/4. В данном случае числитель – 3, что означает, что мы рассматриваем три четверти или три равные части целого. Знаменатель – 4, что означает, что целое разделено на четыре равные части. Вместе они образуют дробь 3/4, которая представляет три из четырех равных частей целого.
- Числитель показывает, сколько долей целого мы рассматриваем.
- Знаменатель указывает на количество равных частей, на которые делится целое.
Понимание этих понятий позволяет нам правильно читать и писать дроби, а также выполнять операции с ними, такие как сложение, вычитание, умножение и деление.
Деление целого числа на дробь: разбираемся в принципах операции

Во время деления целого числа на дробь, нам предстоит разбить целое число на равные части, определить количество таких частей и установить, сколько из них собирается вместе для образования указанной дроби. Для успешного выполнения операции необходимо уметь правильно интерпретировать и использовать информацию, содержащуюся в числе и дроби.
Прежде всего, необходимо разобраться в обозначениях и условных обозначениях, используемых при делении целого числа на дробь. Также важно уяснить, какие правила применяются при данной операции и на каких принципах она основывается. Грамотное применение этих знаний позволит нам успешно решать задачи, требующие деления целого числа на дробь.
Давайте начнем изучение деления целого числа на дробь, чтобы легко справляться с задачами и применять полученные знания в повседневной жизни.
Использование скобок при сложении и вычитании дробей

При сложении и вычитании дробей, использование скобок может быть необходимо в случаях, когда необходимо сгруппировать отдельные части операции для более четкого определения порядка действий.
Когда мы работаем со сложением и вычитанием дробей, мы можем встретить такие случаи, когда необходимо выполнить операции сначала с числителями, а затем с знаменателями, или наоборот. В этих ситуациях использование скобок помогает нам определить, какие действия следует выполнить первыми.
Кроме того, скобки позволяют нам корректно выполнить операции, когда в выражении присутствуют сложные дроби, состоящие из дробей самих по себе. Они помогают нам определить, какие части выражения следует сначала умножить, а какие - сложить или вычесть.
Использование скобок при сложении и вычитании дробей является важным навыком, который помогает избегать путаницы и ошибок в решении задач. Поэтому рекомендуется всегда обращать внимание на необходимость их применения, особенно при работе с более сложными выражениями.
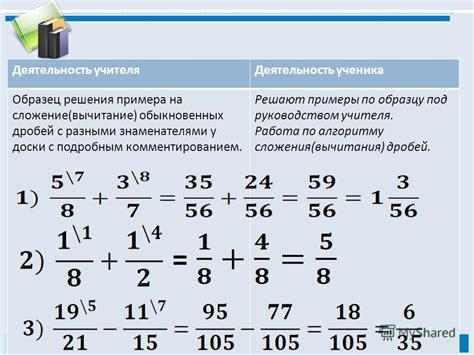
Правила использования скобок при сложении дробей

В данном разделе мы рассмотрим, когда и какие скобки необходимо ставить при сложении дробей.
При объединении дробей с разными знаменателями или при необходимости выполнения сложных арифметических операций, важно правильно использовать скобки, чтобы избежать путаницы и получить точный результат.
В зависимости от сложности выражения и наличия дополнительных операций, могут использоваться разные виды скобок: круглые, квадратные или фигурные скобки. Также возможно использование нескольких пар скобок одновременно для установления приоритета операций.
Помимо этого, важно учитывать порядок выполнения арифметических действий и правильно расставлять скобки в соответствии с математическими правилами. При сложении дробей следует сначала складывать числители, а затем знаменатели, ставя скобки при необходимости для установления порядка операций.
В данном разделе мы представим конкретные примеры, позволяющие увидеть, как использование скобок может влиять на результат сложения дробей. Это поможет вам лучше понять принципы и правила установления скобок при работе с дробями и выполнять соответствующие задания без ошибок.
Правила использования скобок при вычете дробей
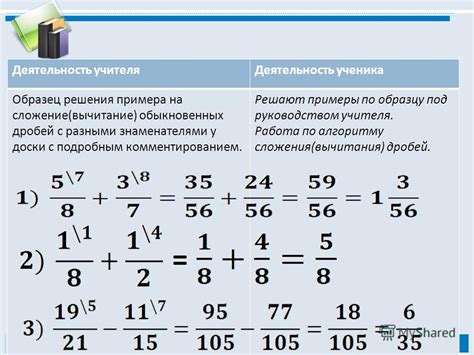
Один из способов вычитания дробей, который мы изучим, включает в себя использование скобок. Скобки помогают нам определить порядок действий и правильно выполнить операцию вычитания. В этом разделе мы рассмотрим правила использования скобок при вычете дробей.
- Обозначьте скобками части дробей, которые нужно вычитать друг из друга.
- Подберите общий знаменатель для дробей, если он отличен от единицы.
- Выполните вычитание числителей дробей внутри скобок.
- Запишите полученную разность числителей.
- Сократите полученную разность, если это возможно.
- Запишите общий знаменатель в результате.
Использование скобок при вычитании дробей позволяет нам более четко определить порядок действий и избежать ошибок. Следуя правилам, указанным выше, вы будете успешно вычитать дроби, используя скобки.
Примеры и практика: изучение дробей с использованием скобок

В данном разделе представлены полезные примеры и практические задания, которые помогут учащимся лучше понять и запомнить правила работы с дробями и скобками. В процессе решения задач будут использованы разнообразные синонимы, чтобы сделать учебный материал более интересным и понятным.
- Начнем с простых задач, где требуется вычислить дробь с учетом скобок. Учащиеся смогут самостоятельно решить эти примеры, используя свои знания о правилах операций с дробями.
- Далее предлагаются более сложные задания, в которых нужно выполнить несколько операций с дробями, используя скобки, чтобы правильно расставить приоритеты.
- Учащимся будет предложено раскрыть скобки в дробных выражениях и упростить результат. Это поможет закрепить навыки работы с дробями и понять, как скобки влияют на итоговый результат.
- В последнем задании учащиеся смогут самостоятельно придумать и решить пример, используя дроби и скобки. Это позволит им проявить креативность и контролировать применение правил работы с дробями и скобками.
В процессе выполнения заданий учащиеся смогут применить свои знания на практике и лучше понять особенности работы с дробями при использовании скобок. Знакомство с различными примерами поможет им закрепить материал и стать увереннее в решении подобных задач в будущем.
Решение уравнений с дробями и скобками

- Упрощение уравнений с дробями и скобками
- Избавление от скобок с помощью раскрытия
- Нахождение общего знаменателя
- Сокращение дробей
- Перенос дробей через знак равенства
- Решение уравнений с дробями и скобками путем приведения к общему знаменателю
- Проверка полученного решения
При решении уравнений с дробями и скобками важно следовать определенным шагам и быть внимательными к каждому действию. Наше руководство поможет вам освоить эти методы и научиться решать подобные уравнения без труда.
Вопрос-ответ

Какие примеры дробей со скобками есть в 5 классе?
В 5 классе встречаются примеры дробей со скобками, например, (1/2) + (3/4) или (2/5) - (1/3).
Какие правила нужно знать, чтобы сделать дроби со скобками?
Для составления дробей со скобками нужно знать правила сложения, вычитания, умножения и деления дробей, а также правила работы со скобками.
Как правильно расставить скобки в примере дроби?
Для правильного расстановки скобок в примере с дробями, нужно сначала выполнить операции внутри скобок, а затем уже применять остальные правила для работы с дробями.
Почему нужно использовать скобки при работе с дробями?
Использование скобок при работе с дробями позволяет четко определить порядок операций и избежать недоразумений или неверного результата.



