Давайте представим себе, что мы обладаем способностью увидеть мир совершенно по-новому. Мир, в котором цифры, числа и математика становятся градиентами красок на холсте. Используя простые инструменты, мы можем строить удивительные изображения, которые вдохновляют и поражают воображение своей гармонией и симметрией.
Просто представьте, что вы можеет создавать картины, которые в одночасье привлекают взгляды и вызывают восхищение. Узор, который мы сегодня рассмотрим - это невероятно красивая спираль, которая строится с помощью принципа, впервые открытого во Франции в XV веке. Это уникальное сочетание формы и чисел, которое основано на красоте и совершенстве математики.
Звучит сложно? Не волнуйтесь! Здесь мы предоставим вам простое и пошаговое руководство о том, как создать эту волшебную спираль с помощью обычного инструмента, который вам, возможно, уже знаком. Вы узнаете, как использовать Excel, популярную программу для работы с таблицами, чтобы воплотить свои идеи в реальность и удивить своих друзей и коллег ваши навыками визуализации данных.
Введение

В течение предстоящих разделов мы изучим базовые понятия и принципы фибоначчиевой последовательности, а также рассмотрим ее связь с геометрией и формами. Мы также рассмотрим методику создания таблицы со значениями Фибоначчи и демонстрацию построения спирали на основе этих значений с использованием инструментов программы Excel.
Вам не требуется быть математиком или экспертом в Excel, чтобы следовать этим шагам и создать свою собственную спираль Фибоначчи. Вся необходимая информация будет пошагово представлена, и мы обязательно поддержим вас в процессе создания этой захватывающей и красочной математической конструкции.
| HTML теги | Применение |
| <h2> | Заголовок раздела |
| <p> | Абзац с текстовой информацией |
| <table> | Создание таблицы для организации информации |
| <tr> | Строка в таблице |
| <td> | Ячейка в таблице |
Определение и особенности
В данном разделе мы рассмотрим сущность и уникальные характеристики конструкции, на основе которой строится изображение, исключая упоминания конкретных методов и программ, используемых для создания.
Определение этой построенной формы предполагает представление о ее некоторых основных свойствах и общих чертах, которые делают ее уникальной и отличающейся от других подобных конструкций.
Изображение, создаваемое с использованием данной методики, представляет собой последовательность элементов, расположенных в специфическом порядке и с определенными пропорциями между ними.
Одной из особенностей такой построенной формы является ее свойство самоподобия, при котором каждый следующий элемент повторяет основные черты предыдущего, сохраняя пропорции и структуру.
Кроме того, такое изображение обладает свойством присутствия в нем числовых последовательностей, подчиняющихся законам Фибоначчи, что придает ему особую гармоничность и эстетическую привлекательность.
| Свойство 1: | уникальность и отличие от других конструкций |
| Свойство 2: | самоподобие элементов |
| Свойство 3: | присутствие числовых последовательностей по законам Фибоначчи |
Почему спираль Фибоначчи полезна для анализа данных?
Использование спирали Фибоначчи предоставляет ценную информацию при анализе данных и построении графиков. Этот геометрический шаблон позволяет визуализировать и установить связи между числами Фибоначчи и другими параметрами.
Функциональность спирали Фибоначчи заключается в ее способности описывать рост и увеличение чисел последовательности Фибоначчи. Золотое сечение, которое присутствует в спирали Фибоначчи, отражает природу и гармонию чисел Фибоначчи и позволяет использовать спираль для выявления закономерностей в данных.
Спираль Фибоначчи также полезна для анализа данных в сфере финансов. Ее использование позволяет исследовать и прогнозировать цикличность рынка, тренды и поведение ценных бумаг. Анализируя графики, построенные на основе спирали Фибоначчи, можно выявить важные точки разворота и определить возможные уровни поддержки и сопротивления.
Кроме анализа финансовых данных, спираль Фибоначчи также применяется в других областях, таких как архитектура, дизайн и наука о данных. Она помогает создавать гармоничные и пропорциональные композиции, уточнять визуальный анализ данных и строить математические модели с использованием чисел Фибоначчи и их соотношениям.
- Спираль Фибоначчи позволяет визуализировать и установить связи между числами Фибоначчи и другими параметрами.
- Она используется для анализа финансовых данных, графиков ценных бумаг и прогнозирования трендов в рынке.
- Спираль Фибоначчи применяется в архитектуре, дизайне и науке о данных для создания гармоничных композиций и визуального анализа данных.
Практическое применение

Применение формул и алгоритмов может привести к удивительным результатам и применениям в различных областях. В данном разделе мы рассмотрим реальные примеры применения спиралей и чисел Фибоначчи, которые могут помочь в создании эстетичных и функциональных решений.
Приложение в дизайне: Использование спиральных формата может придать уникальность и динамику в дизайне логотипов, иконок и других элементов графического дизайна. Играя с размерами, цветами и текстурами, можно создать впечатляющие и привлекательные визуальные композиции, которые будут выделяться среди остальных.
Программирование и алгоритмы: Последовательность чисел Фибоначчи может быть использована в алгоритмах оптимизации и поиска оптимальных путей. Алгоритмы, основанные на числах Фибоначчи, могут помочь в решении задач, связанных с распределением ресурсов, расчетом временных интервалов и оптимизацией систем.
Финансовая аналитика: Числа Фибоначчи также находят применение в финансовой аналитике и прогнозировании рынков. Они могут использоваться для анализа временных рядов, определения изменений тренда и прогнозирования значений валют, акций и других финансовых инструментов.
Архитектура и строительство: Принципы, лежащие в основе спиралей Фибоначчи, могут быть применены в архитектуре и строительстве при разработке планировки зданий, расстановке элементов интерьера, а также в создании уникальных каркасных конструкций, облегчающих распределение нагрузок.
Математическое моделирование: Спирали Фибоначчи находят применение в математическом моделировании различных процессов, таких как рост растений, распределение семян, формирование геометрических структур и многое другое. Моделирование на основе чисел Фибоначчи помогает понять и описать сложные и уникальные явления, происходящие в природе и науке.
Интересно, насколько часто мы встречаемся с использованием чисел Фибоначчи и спиралей в повседневной жизни, даже не задумываясь об их значимости и ярком применении.
Шаг 1: Создание основы таблицы
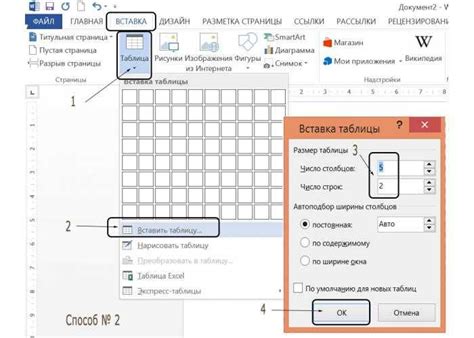
- Откройте программу Excel и создайте новый документ.
- Создайте таблицу, которая будет служить основой для спирали Фибоначчи. Вы можете использовать таблицу размером, например, 10x10 или выбрать размер, наиболее соответствующий вашим потребностям.
- Заполните таблицу числами Фибоначчи. Чтобы это сделать, введите первые два числа Фибоначчи в ячейки A1 и A2, затем используйте формулу "=A1+A2" для расчета следующего числа Фибоначчи и скопируйте эту формулу вниз по столбцу.
- Повторите этот процесс для заполнения остальных столбцов таблицы числами Фибоначчи. Каждый столбец будет представлять собой последовательность чисел Фибоначчи, начиная с разных исходных чисел.
Создание основы таблицы является важным шагом для построения спирали Фибоначчи в Excel. После завершения этого шага, вы будете готовы перейти к следующим шагам, которые включают расчет координат точек спирали и их построение в виде графика или диаграммы.
Оптимизация параметров Excel для эффективной работы
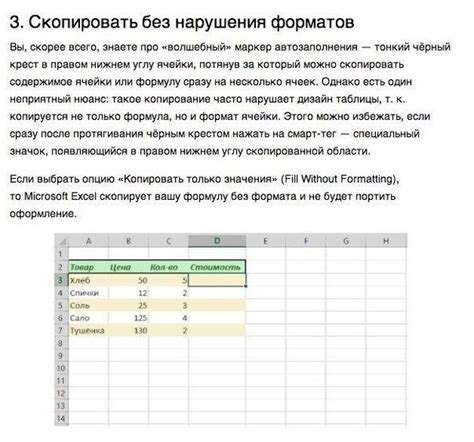
Обеспечьте максимальную производительность работы в Excel, используя эффективные настройки и рекомендации по оптимизации программы.
Настройка Excel для достижения наивысшей эффективности может повысить вашу продуктивность и сократить время, затрачиваемое на выполнение задач. В этом разделе мы рассмотрим несколько важных параметров, которые помогут вам настроить Excel для более быстрой и удобной работы.
1. Размер файлов и форматы:
Один из ключевых факторов, влияющих на производительность Excel, - размер файла. Чем больше файл, тем больше времени потребуется на его открытие и сохранение. Поэтому рекомендуется оптимизировать файлы, уменьшив их размер с помощью следующих методов:
- Используйте упрощенные форматы файлов, такие как .xlsx вместо .xls;
- Удалите ненужные данные, пустые строки или столбцы;
- Ограничьте количество формул и условного форматирования;
- Используйте сжатие файлов при сохранении.
2. Режим расчета формул:
Excel предлагает два основных режима расчета формул: автоматический и ручной. В режиме автоматического расчета Excel будет автоматически пересчитывать формулы при изменении данных. Однако, в больших файлах или при наличии сложных формул, это может замедлить работу программы. В таких случаях можно переключиться на режим ручного расчета и пересчитывать формулы вручную при необходимости.
3. Управление памятью:
Excel использует оперативную память компьютера для обработки данных. Если у вас доступна большая оперативная память, вы можете настроить Excel на использование большего объема памяти для более быстрой работы. Для этого перейдите в настройки Excel и увеличьте значение параметра "Максимальное количество ОЗУ, используемое Excel".
4. Отключение ненужных функций и добавков:
Excel предлагает множество функций и надстроек, некоторые из которых могут использоваться редко или вообще не понадобиться. Отключение ненужных функций и добавков поможет сократить время загрузки программы и повысить общую производительность. Перейдите в настройки Excel и отключите неиспользуемые функции и надстройки, оставив только необходимые для вашей работы.
Оптимизация параметров Excel может значительно повысить вашу производительность и ускорить работу с программой. Примените эти рекомендации и настройки для более эффективного использования Excel в своей работе.
Вычисление числовой последовательности Фибоначчи

Для начала, мы определим первые два числа в последовательности Фибоначчи как 0 и 1. Затем, используя эти два числа, мы сможем вычислить следующие элементы последовательности, следуя простому правилу сложения двух предыдущих чисел. В результате получаем такую последовательность: 0, 1, 1, 2, 3, 5, 8, 13 и т. д.
Для более удобного представления чисел Фибоначчи, мы можем использовать таблицу. Создадим таблицу, в которой первый столбец будет представлять порядковый номер числа в последовательности, а второй столбец - само число Фибоначчи. Мы будем заполнять эту таблицу поэтапно, начиная с первых двух чисел 0 и 1.
| Порядковый номер | Число Фибоначчи |
|---|---|
| 1 | 0 |
| 2 | 1 |
Теперь наша таблица содержит первые два числа Фибоначчи. Чтобы вычислить следующее число, мы просто складываем два предыдущих числа и записываем результат в таблицу. Таким образом, мы продолжаем заполнять таблицу, последовательно вычисляя числа Фибоначчи.
Использование функций и формул Excel в создании спирали Фибоначчи
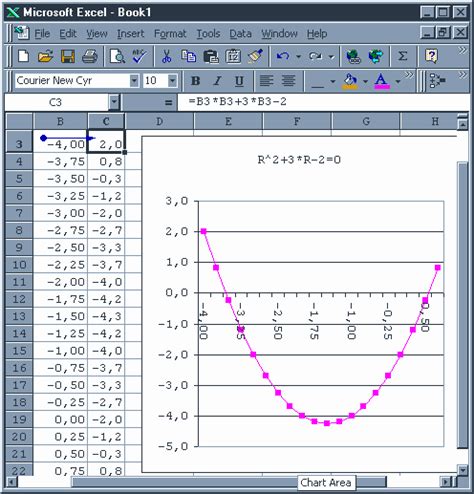
Для построения спирали Фибоначчи в Excel мы используем ряд функций и формул, которые позволяют нам вычислить необходимые значения и построить график спирали. Опишем основные функции и формулы, которые помогут нам в этом процессе.
Первой функцией, которую мы будем использовать, является функция "СУММ", которая позволяет сложить несколько чисел или диапазонов ячеек. С помощью этой функции мы сможем вычислить сумму последовательности чисел Фибоначчи, которая будет использоваться для определения радиуса нашей спирали.
Другой полезной функцией является функция "СДЕЛАТЬ", которая позволяет нам создавать текстовые строки на основе заданных условий. Мы будем использовать эту функцию для создания формулы, которая будет генерировать последовательность чисел Фибоначчи.
Помимо функций, нам понадобятся и различные математические операторы, такие как "+", "*", "/", которые будут использоваться в формулах для вычисления следующих значений в последовательности чисел Фибоначчи.
Кроме того, мы будем использовать формулу "ВПР" для определения координат точек, которые будут использоваться для построения графика спирали. Эта формула позволяет нам вычислить значения по заданной формуле и инкрементировать их при каждом последующем использовании.
Таким образом, с помощью функций и формул Excel, мы сможем построить спираль Фибоначчи, используя вычисленные значения последовательности чисел, а также определить координаты точек для построения графика. Эти инструменты позволяют нам автоматизировать процесс и достичь необходимой точности и эффективности в создании спирали.
3. Построение криволинейной конструкции шаг за шагом

Этот раздел посвящен процессу создания сложной и эстетичной фигуры, которая будет расположена на компьютерном экране или на печатной странице. Вам потребуются несколько инструментов, чтобы достичь желаемого результата, и в этом разделе мы покажем вам каждый шаг на пути к созданию впечатляющей криволинейной конструкции. Мы расскажем о принципах выбора формы и направления линий, а также предложим советы по комбинированию разных элементов. Результат будет изумительным, с тонкими переходами и гармонично сочетающимися формами.
Сначала, определите форму основы для вашей конструкции. Это может быть любая фигура, которую вы изобразите в виде контура, например, круг, треугольник или зигзаг. Затем мы перейдем к созданию основных линий, которые будут определять контуры и направления вашей будущей криволинейной композиции. Здесь важно помнить о принципе плавной зависимости от предыдущих элементов.
Затем мы добавим дополнительные элементы для создания сложности и уникальности вашей криволинейной конструкции. Это могут быть линии, повторяющие контур основы, всплески или пересечения, добавляющие визуальный интерес. Но не забывайте, что каждый дополнительный элемент должен гармонично сочетаться с уже имеющимися, чтобы сохранить целостность и естественность формы.
В конце концов, вы получите завершенную криволинейную конструкцию, которая будет эффектно смотреться на экране или странице. Примените законченную фигуру в своем проекте или исследуйте дополнительные возможности для воплощения своей креативности.
Применение условного форматирования
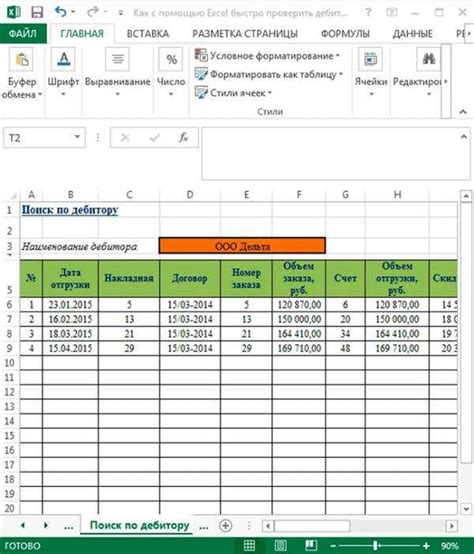
В данном разделе рассмотрим способы применения условного форматирования в приложении Excel. Данная функциональность позволяет автоматически изменять внешний вид ячеек, основываясь на определенных логических условиях.
Для достижения более выразительных результатов и улучшения визуального восприятия данных, мы можем использовать различные условия и сравнения. Например, можно выделить определенные значения ячеек или изменить цвет фона в зависимости от определенного диапазона числовых значений.
Условное форматирование также может быть полезным при поиске и выделении дублирующихся или уникальных значений в таблице данных. Такой подход поможет наглядно выделить особенности или аномалии в наборе данных.
Кроме того, есть возможность использовать условное форматирование для подсветки ошибок или несоответствий. Это помогает обнаружить и исправить ошибки, которые могут возникнуть при внесении данных или выполнении расчетов.
В общем, условное форматирование в Excel предоставляет широкие возможности для визуализации данных и создания более понятной и информативной таблицы. С его помощью можно выделить ключевые значения, провести анализ данных и упростить принятие решений на основе визуальной оценки информации.
Рассмотрим подробнее основные принципы работы с условным форматированием и демонстрационные примеры его применения.
Вопрос-ответ

Как построить спираль Фибоначчи в Excel?
Для построения спирали Фибоначчи в Excel нужно создать таблицу, в которой будут последовательно расположены числа Фибоначчи. Затем, необходимо использовать графические инструменты Excel для построения линий, соединяющих точки с координатами, соответствующими числам Фибоначчи.
Можно ли построить спираль Фибоначчи только с использованием формул в Excel?
Да, можно построить спираль Фибоначчи с помощью формул в Excel. Сначала необходимо задать начальные значения последовательности Фибоначчи в ячейках таблицы. Затем можно использовать формулы, чтобы вычислить координаты точек и отобразить их на графике.
Какая практическая польза может быть от построения спирали Фибоначчи в Excel?
Построение спирали Фибоначчи в Excel может быть полезно для визуализации и изучения числовых последовательностей. Также можно использовать эту спираль для создания декоративных элементов, визуальных эффектов или для анализа данных, например, для расположения объектов на плоскости в определенном порядке.
Какие сложности могут возникнуть при построении спирали Фибоначчи в Excel?
Одной из возможных сложностей при построении спирали Фибоначчи в Excel может быть правильное задание начальных условий для последовательности Фибоначчи. Также может потребоваться некоторое время и терпение для правильного настройки формул и графических инструментов программы.
Как можно улучшить спираль Фибоначчи в Excel, чтобы она выглядела более эстетично?
Для улучшения эстетического вида спирали Фибоначчи в Excel можно изменить ее цвет, толщину линий и добавить различные декоративные элементы. Также можно экспериментировать с увеличением шкалы графика или применить другие графические эффекты, доступные в программе Excel. Это позволит создать более привлекательный и интересный визуальный результат.
Как построить спираль Фибоначчи в Excel?
Для построения спирали Фибоначчи в Excel следует использовать формулы и функции программы. Сначала необходимо создать две ячейки, в которых будут содержаться начальные значения последовательности Фибоначчи. Затем, с использованием функций SUM и OFFSET, нужно создать формулы для последующих ячеек, рассчитывающие следующие значения. После этого следует отрисовать график, используя полученные значения.



