На пути к созданию кривых, прямых или криволинейных графиков, важным этапом является построение прямой через набор заданных точек. Прямая является одним из базовых геометрических объектов, широко применяемых в различных областях науки и инженерии. В этой статье мы рассмотрим эффективные методы и подходы для построения прямой в среде MATLAB на основе заданных точек, без использования стандартных функций.
Взаимосвязь между точками и прямой может быть представлена как линейная аппроксимация. Метод наименьших квадратов является одним из наиболее популярных методов аппроксимации, позволяющим найти наилучшую приближенную прямую по заданным точкам. Использование этого метода поможет нам получить наименьшую сумму квадратов расстояний от каждой точки до прямой.
Один из простых способов построения прямой через заданные точки - использование формулы наклона. Формула наклона поможет нам понять, как изменяется значение координат точек на прямой, а также достичь наилучшей аппроксимации, используя MATLAB. Этот подход позволяет нам найти уравнение прямой через ее наклон и точку, через которую она проходит.
Построение прямой в программе MATLAB с использованием заданных координатных точек
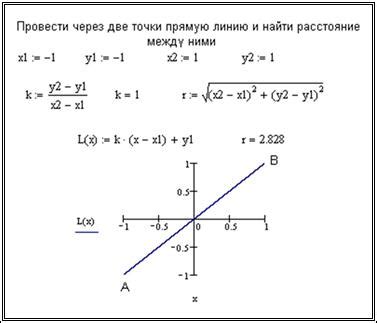
В данном разделе мы рассмотрим процесс построения прямой в программе MATLAB на основе заданных координатных точек. Мы описываем шаги, которые необходимо выполнить, чтобы создать график, отображающий прямую, проходящую через эти точки.
В первую очередь, необходимо импортировать или создать в программе MATLAB набор данных точек, состоящий из входных координат X и соответствующих им Y. Затем мы можем использовать функцию polyfit, которая позволяет аппроксимировать наш набор точек прямой линией методом наименьших квадратов.
Далее, мы можем визуализировать полученную прямую, используя функции plot и hold. Построение графика в MATLAB позволяет наглядно представить зависимость между значениями X и Y, а также увидеть тренд, который демонстрируют наши точки.
Чтобы сделать график более наглядным, мы можем добавить заголовок для обозначения осей координат и подписи для каждой оси. Также можно изменить цвет и стиль линии, чтобы сделать график более уникальным и легко различимым.
Наконец, для создания более точной и понятной прямой, можно добавить дополнительные функции, такие как grid, которая добавляет сетку на графике, или legend, которая позволяет наглядно обозначить каждую прямую, если их несколько.
В итоге, построение прямой в программе MATLAB по заданным точкам сводится к импорту или созданию набора данных, аппроксимации прямой с использованием функции polyfit, визуализации полученной прямой с помощью функции plot, и настройке графика с добавлением заголовков, подписей и стилей линий.
| Функция | Описание |
|---|---|
| polyfit | Функция, используемая для аппроксимации набора точек прямой линией |
| plot | Функция, используемая для создания графика и визуализации прямой |
| hold | Функция, используемая для сохранения предыдущего графика перед добавлением нового |
| grid | Функция, используемая для добавления сетки на график |
| legend | Функция, используемая для создания легенды на графике |
Подготовка рабочей среды
В данном разделе мы рассмотрим необходимую подготовку рабочей среды для построения прямой по заданным точкам в среде MATLAB. Успешное выполнение данной задачи требует правильной настройки и установки соответствующих компонентов, а также знания основных принципов работы с этой средой.
Прежде всего, чтобы начать работу, необходимо установить MATLAB на свой компьютер. После установки и запуска программы, создайте новый проект или откройте существующий, если у вас уже есть готовая рабочая область для работы.
Для построения прямой по заданным точкам нам потребуются математические и графические инструменты. В MATLAB для работы с математическими объектами используются переменные и функции. Создайте соответствующие переменные для представления заданных точек. Это позволит вам более удобно манипулировать данными и проводить необходимые расчеты на них.
Кроме того, необходимо ознакомиться с основными принципами построения графиков в MATLAB. Для этого вам пригодятся функции и команды, позволяющие задавать координатные оси, масштаб графика, а также проводить линии и точки на графике.
Важно помнить, что успешное построение прямой по заданным точкам в MATLAB требует не только умения работать с математическими объектами, но и умения грамотно использовать доступные функции и команды. Используйте документацию и примеры, предоставляемые MATLAB, чтобы лучше понять основы работы и достичь желаемого результата.
| Рекомендации по подготовке рабочей среды |
|---|
| Установите MATLAB на свой компьютер и запустите программу. |
| Создайте новый проект или откройте существующий. |
| Ознакомьтесь с основными принципами работы с математическими объектами в MATLAB. |
| Используйте функции и команды для настройки графической области и построения линий на графике. |
| Консультируйтесь с документацией и примерами MATLAB для достижения желаемого результата. |
Выбор точек для задания линии
Первым шагом в задании точек является определение области, в которой будет строиться линия. Это может быть отрезок на числовой прямой, заданный конечными значениями, или плоскость с определенными границами. Для каждой конкретной задачи следует определить соответствующие ограничения для точек, чтобы получить достоверные результаты.
Затем необходимо выбрать множество точек внутри заданной области, которые будут использоваться для построения прямой. Для этого можно использовать различные приемы: случайное распределение точек, равномерное распределение с постоянным шагом между ними или специальные алгоритмы для выбора оптимальных точек.
Важно учитывать тип данных, с которыми работает матлаб, и выбирать точки, которые являются допустимыми значениями для этих типов. Например, при работе с целыми числами следует выбирать только целочисленные координаты точек.
Выбор точек для задания прямой линии в матлабе является важным этапом работы. От правильно выбранных исходных данных зависит точность и достоверность получаемых результатов. Подходящая выборка точек позволяет построить прямую, которая наилучшим образом описывает заданную область и отражает основные закономерности данных.
Решение системы уравнений для определения коэффициентов прямой

В данном разделе будем рассматривать процесс решения системы уравнений, который позволит определить коэффициенты прямой. Мы будем исследовать математический метод, позволяющий найти значения этих коэффициентов, обеспечивающих наилучшее соответствие прямой данным точкам.
Для начала рассмотрим систему уравнений, описывающую прямую. В данном случае, наша цель – найти уравнение прямой в виде y = ax + b, где a и b – искомые коэффициенты. Для решения такой системы уравнений обычно используется метод наименьших квадратов.
Метод наименьших квадратов предлагает оптимальное решение системы уравнений, которое минимизирует сумму квадратов разностей между значениями y, рассчитанными по уравнению прямой, и реальными значениями y из данных точек. Оптимальные значения a и b найдутся таким образом, чтобы сумма квадратов этих разностей была минимальной.
Для дальнейшего решения системы уравнений следует найти среднее значение x и y по всем точкам данных. Затем находятся значения a и b с использованием формул: а = Σ[(xi - x_avg)(yi - y_avg)] / Σ[(xi - x_avg)^2] и b = y_avg - a*x_avg. Где xi и yi - координаты точек данных, x_avg и y_avg обозначают средние значения x и y соответственно.
Таким образом, решение данной системы уравнений позволит нам найти значения коэффициентов прямой, отражающей лучшую аппроксимацию данных точек. Полученные a и b могут быть использованы для дальнейшего построения прямой и анализа данных.
Составление уравнения прямой

На практике существуют несколько способов составления уравнения прямой. Один из таких методов - метод коэффициентов наклона и точки. Этот метод позволяет определить уравнение прямой, зная координаты любой точки на ней и значение углового коэффициента. Другим способом является метод двух точек, который позволяет определить уравнение прямой, зная координаты двух различных точек, через которые она проходит.
В обоих методах требуется использование математических формул и правил, связанных с определением и выражением уравнений прямых. Благодаря этим формулам, можно точно определить, какую прямую можно построить, а также получить уравнение, описывающее их свойства и связи с другими геометрическими фигурами. Важно помнить, что выбор метода составления уравнения прямой зависит от доступных данных и требований задачи.
| Метод | Описание |
|---|---|
| Метод коэффициентов наклона и точки | Метод, основанный на определении углового коэффициента и координат точки на прямой |
| Метод двух точек | Метод, основанный на определении уравнения прямой по координатам двух различных точек |
Визуализация точек и прямой на графике

В данном разделе мы рассмотрим методы визуализации набора точек и прямой на графике с использованием средства программирования MATLAB. Мы сосредоточимся на том, как наглядно отобразить точки и прямую, чтобы получить детальное представление о связи между ними.
Отображение точек:
Для начала, необходимо иметь набор точек, соответствующих определенной зависимости или совокупности данных. Каждая точка может быть представлена своими координатами на плоскости. Чтобы визуализировать эти точки на графике, можно воспользоваться функцией 'plot' в MATLAB, задавая координаты точек в качестве входных данных. Это позволит построить диаграмму рассеивания, где каждая точка отображается как отдельный символ на графике.
Представление прямой:
Прямая линия может быть определена с помощью уравнения, которое описывает ее свойства и совпадает с математической моделью, используемой для аппроксимации данных. Чтобы визуализировать прямую на графике, можно использовать функцию 'plot', указывая значения x в качестве входных данных и соответствующие значения y, рассчитанные на основе уравнения прямой. Таким образом, прямая будет отображаться на графике в виде линии, соединяющей соответствующие точки.
Комбинированная визуализация:
Дополнительно к отображению отдельных точек и прямой, можно создать комбинированную визуализацию, где точки и прямая представлены на одном графике. Для этого необходимо использовать функцию 'plot' дважды, для точек и для прямой, указывая соответствующие входные данные в каждом случае. Это позволит наглядно увидеть, как прямая проходит через данные точки.
В конечном итоге, визуализация точек и прямой на графике позволяет лучше понять общую зависимость между ними и получить визуальное представление данных. Это полезный инструмент для анализа и визуализации результатов экспериментов, моделей и других количественных данных в MATLAB.
Интерполяция и экстраполяция данных
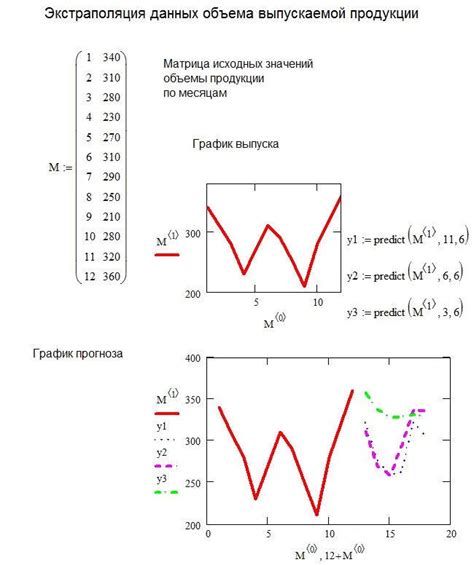
В процессе анализа и обработки данных очень важно иметь возможность предсказывать значения внутри существующих данных (интерполяция) или за их пределами (экстраполяция). Такие методы позволяют заполнить пробелы в данных и прогнозировать будущие значения с высокой точностью.
Интерполяция данных представляет собой процесс нахождения недостающих значений между известными точками на графике или в наборе данных. Это позволяет восстановить пропущенные значения или уточнить прогнозы. В матлабе для интерполяции данных часто используются такие методы, как линейная интерполяция, кубическая интерполяция или использование сплайнов.
Экстраполяция, в свою очередь, позволяет расширить границы данных и предсказать значения за пределами известных точек. Однако, необходимо быть осторожным при экстраполяции, так как она может привести к неадекватным результатам и недостоверным прогнозам. Важно учитывать ограничения данных и использовать адекватные модели для точных прогнозов.
Интерполяция и экстраполяция данных имеют множество применений в различных областях науки и инженерии. Они могут быть использованы для восстановления пропущенных данных в метеорологии, финансах, медицине и других областях. Также эти методы могут быть полезны при анализе временных рядов, построении графиков и прогнозировании тенденций.
Анализ графического представления данных
Изучая график, мы можем увидеть, каким образом точки соединены между собой. Анализируя изменение наклона линии, мы можем оценить степень взаимной зависимости сопоставленных значений. Если линия является строго прямой, это может указывать на линейную зависимость, тогда как кривая линия может указывать на более сложную связь между данными.
Также можно обратить внимание на точность приближения линии к точкам. Чем ближе линия проходит к значениям, тем более соответственными они являются данным. Если точки разбросаны относительно линии, это может указывать на большую неопределенность или наличие случайного фактора в данных.
Более глубокий анализ графика может включать изучение точек-выбросов, которые сильно отклоняются от общего тренда линии. Такие точки могут быть результатом ошибок измерения или являться особыми значениями, требующими отдельного анализа и объяснения. Их исключение или учет может существенно влиять на общую интерпретацию данных.
Наконец, анализ графика также может включать оценку тренда, направления и величины изменения значений. Изучение изменения наклона линии или наличия промежуточных точек может дать представление о характере изменения данных и об их динамике.
Оценка точности аппроксимации

Для правильной оценки точности аппроксимации необходимо учитывать степень соответствия полученной прямой модельным данным. Аппроксимация позволяет приблизить сложную зависимость между переменными с помощью более простой функции, такой как прямая. Оценка точности аппроксимации позволяет использовать прямую как представление для анализа и исследования данных.
В данном разделе будут рассмотрены методы оценки точности аппроксимации, позволяющие определить насколько хорошо прямая, построенная по заданным точкам, соответствует модельным данным. Одним из основных критериев, используемых при оценке точности, является сумма квадратов отклонений предсказанных значений прямой от исходных точек. Чем меньше эта сумма, тем точнее аппроксимация и лучше подходит прямая для представления данных.
Для более точной оценки аппроксимации также используются другие метрики, такие как коэффициент детерминации, который показывает, какую часть дисперсии объясняет модель, и стандартная ошибка оценки, которая позволяет определить, насколько точно прямая предсказывает значения вне заданных точек. Различные методы оценки точности позволяют выбрать наилучшую прямую из нескольких вариантов аппроксимации и провести анализ ее пригодности для дальнейшего использования.
Дополнительные возможности программы MATLAB для работы с линейными зависимостями
В этом разделе рассмотрим несколько дополнительных инструментов и функций, которые предлагает программа MATLAB для работы с линейными зависимостями. Эти возможности помогут не только построить прямую по заданным точкам, но и выполнять более сложные операции с линейными уравнениями и изучать их свойства.
Одним из таких инструментов является функция polyfit, которая позволяет аппроксимировать заданные точки линейной функцией. С помощью этой функции можно определить коэффициенты прямой, которая наилучшим образом приближает заданный набор точек. Такой подход особенно полезен при работе с шумными данными, где точное построение прямой может быть затруднено.
Еще одной полезной функцией является lsqcurvefit, которая позволяет аппроксимировать нелинейные функции линейной моделью. Это может быть полезно, например, при анализе экспериментальных данных с нелинейными зависимостями. Функция lsqcurvefit позволяет находить наилучшую аппроксимацию линейной модели к данным и оценивать параметры этой аппроксимации.
Кроме того, в MATLAB присутствуют функции для работы с матрицами и векторами, которые делают работу с линейными уравнениями более удобной. С помощью этих функций можно выполнить операции по умножению матриц, решению систем линейных уравнений и нахождению собственных значений и векторов матрицы.
Вопрос-ответ

Какие данные нужно задать для построения прямой в Matlab?
Для построения прямой в Matlab необходимо задать координаты двух точек, через которые проходит прямая.
Каким образом можно задать координаты точек в Matlab?
Координаты точек в Matlab можно задать с помощью массивов или векторов. Например, можно использовать два массива, один для значений x, и второй для значений y.



