Многие из нас, хоть и не осознают этого, сталкиваются с NURBS поверхностями практически каждый день. Они скрываются за гладкими линиями автомобилей и яхт, уютными формами мебели, а также придают совершенство архитектурным сооружениям. Но что за технология кроется за этими загадочными буквами?
Математика вечно ведет нас в мир удивительных открытий, и NURBS – не исключение. Полное название этого термина звучит как "Non-uniform rational B-spline", что можно перевести как "неравномерная рациональная B-сплайновая кривая". Впечатляющее название отображает суть технологии, стоящей за этим термином.
Технология NURBS, используемая в компьютерной графике и дизайне, позволяет создавать плавные и красивые геометрические объекты, обладающие сложными формами и деталями. Сочетая в себе мощь математики и творчество дизайнера, NURBS считается одним из самых эффективных инструментов для создания сложных трехмерных моделей.
Основы создания Nurbs-объектов
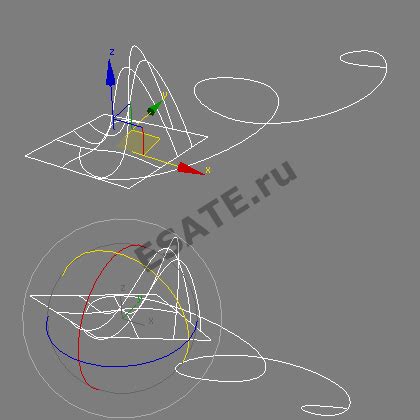
Основные принципы построения Nurbs-поверхностей включают в себя определение контрольных точек, весов и степеней кривых. Контрольные точки - это набор точек в пространстве, определяющих форму поверхности. Веса присваиваются этим точкам и позволяют контролировать их влияние на форму поверхности, а степени кривых определяют гладкость и детализацию поверхности.
Важным аспектом при построении Nurbs-поверхностей является выбор оптимального числа и расположения контрольных точек. Чем больше точек, тем более сложную и детализированную поверхность можно создать. Однако слишком большое число точек может привести к сложностям в управлении и обработке объекта. Поэтому необходимо найти баланс между детализацией поверхности и ее управляемостью.
Для удобства работы с Nurbs-поверхностями используются различные форматы файлов, такие как IGES, STEP и STL. Они позволяют сохранять и обмениваться моделями поверхностей между различными программами для работы с трехмерной графикой.
| Преимущества Nurbs-поверхностей | Недостатки Nurbs-поверхностей |
|---|---|
| Плавные и гибкие формы | Сложность создания и управления |
| Высокая степень детализации | Возможность появления неестественных артефактов |
| Универсальность использования | Большие требования к вычислительным ресурсам |
Что такое Nurbs поверхности и их предназначение
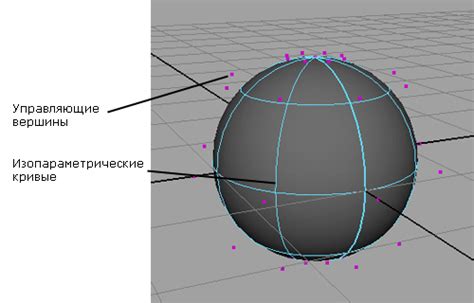
Нurbs, что расшифровывается как Non-Uniform Rational B-Splines (Неравномерные рациональные Вееры-сплайны), представляют собой эффективный способ описания плавных и сложных трехмерных форм. Они широко применяются в создании кривых и поверхностей благодаря своим особенностям и достоинствам.
Основное предназначение Nurbs поверхностей заключается в точном определении формы объекта с использованием узлов и контрольных точек. Они обладают гибкостью в изменении формы, что позволяет адаптировать поверхности под требования проекта. Благодаря их способности представлять сложные формы, такие как органические объекты или поверхности с большим количеством деталей, Nurbs поверхности стали незаменимым инструментом в различных областях, включая архитектуру, дизайн, медицину и игровую индустрию.
Для работы с Nurbs поверхностями важно понять основные понятия, такие как степень кривых, алгоритм де-Бура и весовые коэффициенты. Эти концепции позволяют создавать сложные формы с высокой степенью контроля и точности.
Использование Nurbs поверхностей требует умения работать с специализированными программами и инструментами, такими как 3D-редакторы или инженерные пакеты. Понимание принципов Nurbs и опыт их применения являются важными навыками для профессионалов, занимающихся визуализацией и 3D-моделированием.
Структура и особенности геометрических кривых и поверхностей в системе Nurbs
Структура кривых и поверхностей: Nurbs поверхности состоят из кривых, которые в свою очередь состоят из узлов и контрольных точек. Узлы определяют параметрическое распределение точек на кривой или поверхности, а контрольные точки определяют геометрию кривой или поверхности.
Особенности Nurbs поверхностей: Nurbs поверхности обладают высокой гибкостью и точностью в описании сложных форм. Они способны описывать как плоские, так и трехмерные объекты, а также включать в себя переходы между гладкими и угловатыми областями. Кроме того, Nurbs поверхности поддерживают дополнительные параметры, такие как вес контрольных точек, что позволяет управлять интенсивностью влияния каждой точки на форму поверхности.
Преимущества использования Nurbs поверхностей: Эта технология предлагает ряд преимуществ, включая высокую точность и гибкость в моделировании сложных форм, возможность создания плавных переходов между различными областями, а также возможность контроля над структурой поверхности для достижения определенных эффектов. Кроме того, редактирование и модификация Nurbs поверхностей является относительно простым и наглядным процессом.
Заключение: Понимание структуры и характеристик Nurbs поверхностей позволяет эффективно использовать эту технологию в создании сложных геометрических объектов. Надлежащее использование узлов, контрольных точек, а также применение дополнительных параметров, обеспечивает высокую точность, гибкость и контроль при моделировании поверхностей в системе Nurbs.
Методы и инструменты формирования кривых и поверхностей высокой степени точности

В этом разделе рассмотрим разнообразные подходы и инструменты, которые можно применять для создания сложных и точных кривых и поверхностей. Будут представлены методы моделирования, которые помогут достичь высокой степени детализации и плавности создаваемых объектов.
Геометрическое моделирование
Одним из наиболее распространенных методов создания Nurbs поверхностей является геометрическое моделирование. Оно позволяет визуально редактировать форму объектов, используя интуитивные инструменты, такие как перетаскивание точек или вытягивание кромок. Геометрическое моделирование предоставляет разнообразные операции, такие как сглаживание кривых, соединение элементов и создание сложных композиций.
Математическое моделирование
Для создания более сложных форм и поверхностей, математическое моделирование использует алгоритмы и уравнения, основанные на математических принципах. Одним из наиболее популярных методов является NURBS (Non-Uniform Rational B-Splines) – математическая модель, которая представляет кривые и поверхности в виде управляющих точек, с помощью которых можно контролировать и изменять форму объектов. Математическое моделирование позволяет создавать более сложные и точные формы, нежели геометрическое моделирование, но требует более высокого уровня математической подготовки и понимания.
Компьютерное моделирование
С развитием компьютерных технологий появились специализированные программы и инструменты для создания Nurbs поверхностей. Эти программы предоставляют широкий набор инструментов и функций, которые позволяют создавать и редактировать кривые и поверхности. Также они обладают мощными алгоритмами для автоматического расчета формы объектов и оптимизации их параметров. Компьютерное моделирование значительно упрощает процесс создания сложных и точных кривых и поверхностей, а также позволяет быстро прототипировать и визуализировать результаты.
Таким образом, выбор методов и инструментов для создания Nurbs поверхностей зависит от уровня желаемой точности и сложности объекта. Геометрическое моделирование позволяет быстро создавать и редактировать формы, математическое моделирование обеспечивает более точные результаты, а компьютерное моделирование объединяет удобство использования с высокой точностью и эффективностью работы.
Примеры применения Nurbs поверхностей в индустрии и дизайне
В данном разделе рассмотрим несколько реальных примеров использования Nurbs поверхностей, мощного инструмента, который нашел свое применение в различных отраслях индустрии и дизайне.
1. Автомобильный дизайн: Nurbs поверхности активно применяются в автомобильной индустрии для создания плавных кривых кузовов, гладких элементов интерьера и эргономичных рукояток. Благодаря гибкости и точности, Nurbs поверхности позволяют дизайнерам создавать эстетически привлекательные и функциональные автомобильные детали.
2. Аэрокосмическая отрасль: Nurbs поверхности являются неотъемлемой частью процесса проектирования и моделирования для создания аэродинамических обтекателей, винтовых лопастей, корпусов спутников и других компонентов. Благодаря гибкости и возможности создания сложных кривых, Nurbs поверхности позволяют инженерам создавать оптимальные формы для достижения высокой эффективности и производительности.
3. Медицинская отрасль: Nurbs поверхности применяются в медицине для моделирования и создания протезов, ортезов и индивидуально-изготовленных медицинских изделий. Гибкость и точность Nurbs поверхностей позволяют реализовывать индивидуальные потребности пациентов, обеспечивая комфорт и эффективность используемых устройств.
4. Промышленный дизайн: Nurbs поверхности широко применяются в разработке промышленных товаров, таких как мебель, электроника, бытовая техника и другие. Они позволяют дизайнерам создавать эргономичные и эстетически привлекательные формы, учитывая требования функциональности, производства и эргономики.
В приведенных выше примерах видно, что использование Nurbs поверхностей нашло применение в различных областях индустрии и дизайна, что подчеркивает их важность и эффективность как инструмента для создания сложных, гладких и эстетически привлекательных форм.
Вопрос-ответ

Что такое Nurbs поверхности?
Nurbs (Non-Uniform Rational B-Splines) - это математическая модель для создания и представления кривых и поверхностей в графике и компьютерной графике.
Какие программы позволяют строить Nurbs поверхности?
Существует множество программ для создания Nurbs поверхностей, таких как Rhinoceros 3D, Autodesk Maya, 3ds Max и другие.
Какие параметры влияют на форму Nurbs поверхности?
Форма Nurbs поверхности зависит от положения и количества контрольных точек, их весов, а также интерполяционных функций, определяющих форму кривой или поверхности.
Какие преимущества имеют Nurbs поверхности по сравнению с другими типами поверхностей?
Nurbs поверхности обладают высокой гибкостью и позволяют более точное представление кривых и поверхностей с помощью относительно небольшого количества контрольных точек. Они также обеспечивают плавные переходы между кривыми и поверхностями и поддерживают адаптивное изменение их геометрии.



