Когда мы пишем программы, мы оперируем различными типами данных, включая числа. Использование этих чисел требует понимания основных арифметических операций: сложение, вычитание, умножение и деление. Однако, иногда возникают ситуации, когда нам нужно работать с отрицательными числами, и вот здесь появляется дополнительный код.
Дополнительный код - это способ представления отрицательных чисел в компьютере. Он используется для выполнения операций с этими числами и сохранения их в памяти компьютера. Дополнительный код позволяет работать с отрицательными числами так же, как и с положительными, используя те же арифметические операции.
Построение дополнительного кода отрицательного целого числа является процессом, который выполняется компьютером перед выполнением операции с этим числом. Он обеспечивает представление числа в формате, понятном для компьютера, и позволяет ему выполнять нужные арифметические операции.
Дополнительный код представляет собой измененную версию исходного числа, в которой все биты инвертированы (перевернуты), а затем к полученному числу прибавляется единица. Это создает отрицательное представление числа, которое может быть использовано для выполнения операций.
Методы формирования отрицательного значения путем изменения информации числа

В данном разделе будут рассмотрены различные приемы и методы для образования отрицательного значения путем модификации информации числа. Здесь будут представлены способы изменения числа, чтобы получить его дополнительный код, что позволит работать с отрицательными числами в компьютерных системах.
Будут рассмотрены способы, при которых с использованием определенных операций и манипуляций происходит изменение битового представления числа, что приводит к получению его дополнительного кода. Данные методы представляют собой автоматические алгоритмы, которые позволяют эффективно осуществлять операции с отрицательными числами, сохраняя при этом их точность и корректность вычислений.
Важно отметить, что каждый из рассматриваемых методов имеет свои особенности, преимущества и недостатки. В данном разделе будут представлены подходы, основанные на различных математических операциях и логических операторах. Будут также проанализированы их эффективность и применимость для различных видов чисел, чтобы обеспечить наиболее оптимальное решение при работе с отрицательными целыми числами.
Изучение данных методов является важной составляющей понимания и использования дополнительного кода в современных компьютерных системах. Раздел позволит разобраться в принципах получения отрицательного значения числа и применять эти знания для решения разнообразных задач в области программирования и вычислительной техники.
Использование обратного кода
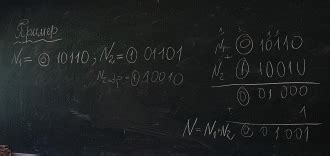
Для использования обратного кода необходимо преобразовать отрицательное число в его обратное представление. В таком представлении биты числа инвертированы, то есть 0 заменяется на 1, а 1 на 0. Кроме того, старший бит числа, который отвечает за его знак, также инвертируется. Полученное обратное представление отрицательного числа можно использовать для выполнения различных операций, таких как сложение, вычитание и сравнение чисел.
- Обратный код обладает рядом преимуществ, среди которых можно выделить экономию памяти и простоту в реализации.
- Однако, обратный код также имеет некоторые ограничения, связанные с работой с нулем и проблемами при выполнении операций умножения и деления.
Использование обратного кода является важной темой в области компьютерных систем и может быть полезным для понимания работы числовых представлений в компьютерах. Понимание особенностей обратного кода позволяет более эффективно работать с отрицательными числами и применять их в различных алгоритмах и системах.
Метод формирования обратного значения путем инвертирования битов и добавления единицы

Данный раздел рассмотрит метод построения обратного значения при отрицательном числе, основанный на применении операции побитового отрицания и последующем добавлении единицы. Этот подход позволяет получить обратное значение числа, не прибегая к использованию специальных алгоритмов или математических преобразований.
Применение алгоритма двоичного дополнения для получения обратного значения положительного числа

Суть алгоритма заключается в том, что все биты исходного числа инвертируются (меняются с 0 на 1 и наоборот), а затем к полученному значению прибавляется единица. Таким образом, получается дополнительное кодирование числа, которое можно оперировать в компьютерных вычислениях.
- Шаг 1: Инвертирование битов
- Шаг 2: Прибавление единицы
- Шаг 3: Получение дополнительного кода
В результате применения алгоритма двоичного дополнения, значение положительного числа изменяется таким образом, что его представление становится аналогичным представлению отрицательного числа в двоичной системе. Такое преобразование позволяет упростить вычисления и операции со знаковыми числами.
Вопрос-ответ

Как можно построить дополнительный код отрицательного целого числа?
Для построения дополнительного кода отрицательного целого числа следует выполнить преобразование в двоичное представление данного числа и инвертировать все его биты (заменить 0 на 1 и 1 на 0). Затем, прибавить к полученному числу 1. Таким образом, получится дополнительный код заданного отрицательного числа.
Почему необходимо инвертировать все биты и прибавить 1 для построения дополнительного кода отрицательного числа?
Инвертирование всех битов и добавление единицы в дополнительное число используется для создания представления отрицательных чисел в компьютерных системах. При таком представлении возможно выполнение операций сложения и вычитания как для положительных, так и для отрицательных чисел с использованием схожих алгоритмов.
Какие проблемы могут возникнуть при построении дополнительного кода отрицательного целого числа?
При построении дополнительного кода отрицательного числа могут возникнуть проблемы связанные с переполнением и ошибочным представлением числа. Например, если число превышает допустимый диапазон, возможно обрезание значащих битов и ошибочное представление числа. Также, некорректное выполнение операции инверсии и добавления единицы может привести к неправильному результату.



