Многие ученики 9 класса сталкиваются с тем, что изучение теории вероятности требует от них старания и тщательной подготовки. Представьте себе, что в одну мгновенье вы можете оценить вероятность события, предсказать его исход и сделать осознанный выбор. Умение работать с вероятностями не только обогатит вашу жизнь, но и поможет вам успешно справиться с заданиями по математике на ОГЭ.
Но как же подготовиться к этому испытанию, не пользуясь услугами репетиторов и специальных курсов? Первый шаг - это осознать важность данного раздела математики и его применение в повседневной жизни. Ведь вероятность окружает нас повсюду: в событиях, происходящих вокруг нас, в деловых решениях и в нашем собственном принятии решений.
Второй шаг состоит в освоении основных понятий вероятности. Необходимо понять смысл таких понятий, как случайное событие, элементарное событие, вероятность, условная вероятность, зависимые и независимые события. Умение точно определить событие и правильно расчитать вероятность его наступления - вот основные навыки, которые вам потребуются на экзамене.
Роль изучения теории вероятности в 9 классе
Значимость освоения принципов и законов теории вероятности в начальном этапе обучения студентов не может быть преуменьшена или недооценена. Это раздел математики, который помогает формировать критическое мышление, развивает навыки логического рассуждения, а также способствует углубленному пониманию окружающего мира.
Получение навыков оценки вероятности - одна из ключевых целей изучения этого раздела математики. Ученикам предоставляются возможности научиться предвидеть вероятность наступления событий и анализировать их, что является незаменимым навыком в жизни каждого человека. Разбираясь в принципах вероятности и ее расчетах, студенты могут принимать взвешенные и обоснованные решения в условиях неопределенности и вероятности.
Развитие логического мышления также является бесценным преимуществом изучения теории вероятности. Раздел математики позволяет учиться строить доказательства и аргументированные рассуждения, анализировать информацию и находить связи между различными событиями. Логическое мышление, развитое в ходе изучения теории вероятности, полезно не только в математике, но и в различных сферах жизни, таких как научное исследование, принятие решений и решение проблемных ситуаций.
Формирование понимания окружающего мира является непосредственным результатом изучения теории вероятности. Раздел математики помогает ученикам понять, как принципы вероятности работают в реальной жизни, как они применяются для прогнозирования событий и принятия решений. Знание вероятности позволяет студентам разбираться в статистических данных, оценивать риски и вероятности различных исходов. Таким образом, изучение теории вероятности предоставляет учащимся возможность получить глубокое понимание окружающего мира и использовать его в повседневной жизни.
Планирование времени и ресурсов: эффективная подготовка к ОГЭ по теории вероятности
Организуйте свое время. Разработайте расписание, которое позволит вам регулярно заниматься изучением теории вероятности. Установите приоритеты и определите блоки для каждого аспекта предмета, например, вероятность событий, комбинаторика или теоремы. Разбейте главные темы на более мелкие подтемы и запланируйте время на изучение каждой из них.
Помните о ресурсах. Найдите и соберите надежные учебные материалы, которые могут помочь вам в подготовке к ОГЭ по теории вероятности. Используйте учебники, пособия, интернет-ресурсы и другие источники информации, которые объясняют концепции и принципы теории вероятности. Уделите особое внимание решению задач разной сложности, поскольку ОГЭ часто включает задачи, требующие применения полученных теоретических знаний.
Используйте различные методы. Варьируйте свои методы изучения теории вероятности, чтобы улучшить понимание и запоминание материала. Сочетайте чтение, запись, наблюдение, объяснение и решение задач. Применяйте методику активного обучения, путем регулярных практических тренировок и самостоятельного решения задач. Участие в групповых занятиях или консультациях с учителем также может быть полезным.
Оцените свой прогресс. Регулярно проверяйте свои знания и навыки, чтобы оценить свой прогресс и выявить возможные пробелы в знаниях. Решайте пробные тесты, задания и самостоятельные работы, чтобы привыкнуть к формату ОГЭ. Уделяйте внимание ошибкам и разбирайте их, чтобы избегать повторения в будущем.
Запланируйте повторение и отдых. Уделите время для повторения основных концепций и принципов, а также для закрепления навыков решения задач. Разделите свое время на периоды активной работы и периоды отдыха, чтобы избежать переутомления и сохранить мотивацию до самого ОГЭ.
Эффективное планирование времени и ресурсов в процессе подготовки к ОГЭ по теории вероятности поможет вам оптимально использовать доступные ресурсы, укрепить свои знания и повысить уверенность в себе перед экзаменом.
Рациональное распределение времени для успешной подготовки к ОГЭ по теории вероятности
1. Анализуйте программу
Перед тем, как распределить время на подготовку, важно внимательно изучить программу ОГЭ и понять, какие темы и трудности она включает. Выделите основные темы и разбейте их на подтемы для более детального изучения.
2. Определите приоритеты
После анализа программы определите, какие разделы требуют большего внимания и усиленной подготовки. Уделите больше времени сложным и непонятным темам, чтобы лучше их освоить.
3. Разбивайте на части
Разбейте общий период подготовки на небольшие отрезки времени. Например, недели или дни. Определите, сколько времени вы готовы уделять ежедневно и разделите его на равные части для каждого раздела программы. Такая система поможет вам усваивать информацию постепенно и систематически.
4. Практика важна
Не забывайте уделять достаточное время для решения практических задач. Возьмите примеры заданий из предыдущих годов, учебников или интернет-ресурсов и решайте их регулярно. Практика поможет вам лучше понять и применять изученные темы.
5. Не забывайте о повторении
Включите в свое расписание время для повторения уже изученных тем. Повторение помогает закрепить знания и обеспечить их долговременное сохранение.
Соблюдение этих рекомендаций поможет вам эффективно распределить свое время и обеспечить успешную подготовку к ОГЭ по теории вероятности.
Изучение основных понятий

В данном разделе будет рассмотрено описание и объяснение ключевых терминов и понятий, связанных с предметом теории вероятности в 9 классе.
В этом разделе мы рассмотрим базовые понятия, необходимые для понимания основ вероятностного анализа. Здесь вы сможете ознакомиться с основными терминами, которые используются в теории вероятности. Мы приведем их определения и проиллюстрируем на примерах, чтобы вы лучше поняли, как эти понятия работают и как их применять.
Основные понятия включают: случайные события, исходы, вероятности событий, условные вероятности, независимость событий и другие. Каждое понятие будет разобрано отдельно, в их последовательном изучении будет понятно, как они связаны между собой и как они применяются в решении задач по теории вероятности.
Понимание этих ключевых терминов является основой для усвоения и применения теории вероятности на практике. Тщательное изучение основных понятий сделает вас готовыми к решению задачи по теории вероятности в ОГЭ и поможет вам успешно справиться с экзаменом.
Обеспечение глубокого понимания основных понятий в области вероятности
Одним из ключевых понятий в теории вероятности является "вероятность". Она отражает степень возможности наступления события, и может быть определена как отношение числа благоприятных исходов к общему числу исходов. К примеру, при бросании правильной монеты вероятность выпадения орла равна 0.5, так как есть два равновероятных исхода: выпадение орла или решки.
Важным понятием, связанным с вероятностью, является "событие". Событие - это определенный результат или исход, который может произойти при проведении эксперимента или ситуации. Например, событием может быть выпадение четного числа при броске кубика, или получение орла при броске монеты. Вероятность события определяется как отношение числа благоприятных исходов, которые приводят к данному событию, к общему числу исходов.
Еще одним важным концептом является "случайная величина". Случайная величина представляет собой числовую характеристику, которая зависит от результатов случайного эксперимента. С помощью случайных величин мы можем описывать и изучать вероятности различных исходов. Для примера, при броске двух кубиков случайная величина может представлять собой сумму чисел на выпавших гранях. Мы можем рассчитать вероятность получения каждой возможной суммы и использовать это для решения разных задач.
Проверка навыков и практическое применение

Способ проверки и укрепления знаний по теме "вероятности" в 9 классе включает в себя практические задания и тестирование. Эти методы помогут учащимся лучше понять и усвоить теоретические понятия, а также научиться применять их на практике.
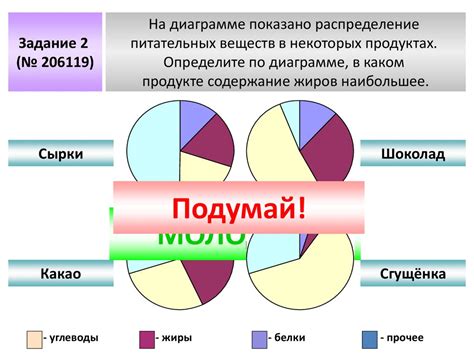
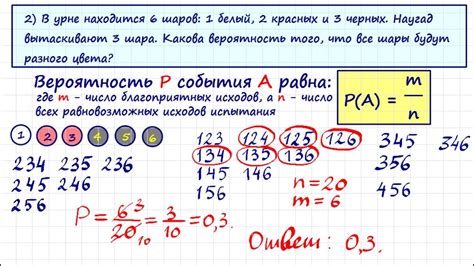
Практические задания могут включать в себя различные ситуационные задачи, где учащийся должен применить полученные знания о вероятности. Например, решение задач на определение вероятности выбора определенной карты из колоды или вероятности выпадения определенного числа на игральной кости. Это позволяет ученикам на практике применить теоретические знания и развить логическое мышление.
Важным этапом подготовки к ОГЭ по теории вероятности является тестирование. Тесты позволяют проверить уровень знаний, помогают выявить слабые места и разработать стратегию дальнейшей подготовки. В процессе тестирования учащийся может встретиться с различными заданиями, которые подразумевают анализ условия, применение формул и проверку своих ответов.
Использование практических заданий и тестирования дает возможность ученикам не только понять теоретический материал, но и научиться его применять на практике. Это позволяет не только справиться с заданиями ОГЭ, но и развить навыки анализа, логического мышления и применения математических знаний в реальных ситуациях.
Зачем решать все задачи по теории вероятности перед Государственной итоговой аттестацией?

Подготовка к Государственной итоговой аттестации требует основательного изучения различных тем, включая теорию вероятности. Однако возникает вопрос: необходимо ли решать все задачи по этой теме?
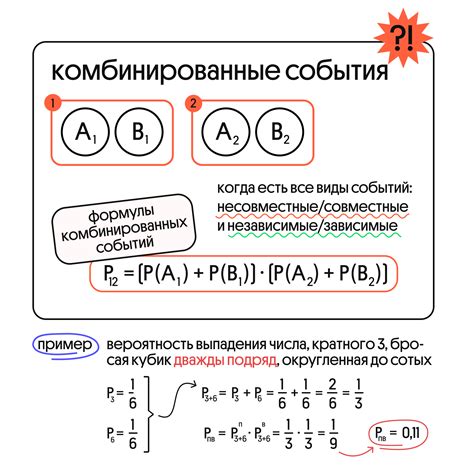
Когда мы говорим о необходимости решать все задачи по теории вероятности, мы не ограничиваемся простым запоминанием определений и формул. Напротив, решение задач позволяет углубить понимание сути вероятностных явлений и развить логическое мышление.
Решение разнообразных задач по теории вероятности помогает студентам усвоить основные концепции и применять их на практике. В процессе решения задач возникает необходимость применять такие понятия, как вероятность, событие, случайная величина и другие. Это позволяет закрепить полученные знания и умения, а также развить навыки рассуждений и анализа.
Кроме того, решение задач помогает выработать стратегию подхода к поиску решения. Каждая задача представляет собой новую ситуацию, требующую выхода за рамки шаблонных методов решения. Ответ на задачу может быть найден различными способами, поэтому решение задач требует гибкости мышления и умения применять ранее изученные методы и принципы.
Несомненно, не все задачи являются одинаково важными для подготовки к Государственной итоговой аттестации. Некоторые из них могут быть более сложными или редко встречающимися в экзаменационных заданиях. Однако, решение разнообразных задач позволяет овладеть широким набором навыков и быть готовым к любым вариациям задач, которые могут встретиться на экзамене.
Итак, решение всех задач по теории вероятности перед Государственной итоговой аттестацией не только позволяет закрепить полученные знания и развить навыки, но также способствует более глубокому пониманию теории вероятности в целом.
Вопрос-ответ

Какие темы по теории вероятности стоит изучить перед подготовкой к ОГЭ?
Перед подготовкой к ОГЭ по теории вероятности рекомендуется изучить следующие темы: основные понятия (элементарное событие, исход, вероятность), способы вычисления вероятности (геометрический, алгебраический и комбинаторный методы), теоремы о вероятности (теорема сложения, теорема умножения, теорема Байеса), условная вероятность, независимость событий, задачи на нахождение вероятности событий, составление деревьев возможных исходов.
Какой подход лучше использовать при решении задач по теории вероятности?
При решении задач по теории вероятности рекомендуется использовать систематический подход. Сначала необходимо четко определить условия задачи и выделить все необходимые данные. Затем следует выбрать соответствующий метод вычисления вероятности (геометрический, алгебраический или комбинаторный) и применить его для решения задачи. Важно не забывать проверять полученные результаты на логическую обоснованность и корректность.
Существуют ли какие-то стратегии для успешной подготовки к ОГЭ по теории вероятности?
Да, существуют некоторые стратегии, которые помогут успешно подготовиться к ОГЭ по теории вероятности. Во-первых, рекомендуется регулярно повторять и закреплять изученный материал, делая упражнения и решая задачи разной сложности. Во-вторых, полезно использовать дополнительные пособия и учебники, которые содержат теоретический материал и большое количество задач для тренировки. Также стоит обратить внимание на разбор типовых ошибок и трудных моментов, чтобы избегать их в дальнейшем. В-третьих, полезно решать пробные тесты и ОГЭ-форматы заданий, чтобы оценить уровень подготовки и выработать стратегию решения задач на время. Кроме того, важно не забывать о правильной организации своего рабочего времени, давая достаточно времени на подготовку к теории вероятности, и об организации здорового образа жизни.



