Математика - наука, которая изучает множество явлений и закономерностей внутри стройной системы чисел. В этой статье мы погрузимся в мир целых и натуральных чисел, изучая их различия и правила, которые им присущи. Открытый кругозор и понимание сущности этих двух понятий помогут нам легче познать основы арифметики и, возможно, облегчить жизнь, переступая через цифровые пороги нашего мира.
Целые числа - это наборы чисел, которые демонстрируют полное пространство числового континуума в обе стороны, включая как отрицательные, так и положительные значения. Они, в отличие от натуральных чисел, стоят на двух плечах: положительном и отрицательном. Нельзя пройти мимо целых чисел, не скользив вниз по ним или не забравшись вверх. Эти числа являются важной составляющей нашей повседневной жизни, пронизывая различные аспекты математики, науки и даже философии.
Натуральные числа же - это более простая, "очищенная" версия числового языка, где упрощение заключается в отсутствии отрицательных значений. Они нежно обволакивают нас с самого рождения и сопровождают на протяжении всей нашей жизни. Нужно быть благодарными этим небольшим цифрам, ведь благодаря ним мы можем определить количество чего-либо, пересчитать наши результаты и даже отражать наш рост или падение в правильном соотношении.
Основные понятия и характеристики натуральных и целых чисел
Когда речь идет о числах, мы обычно говорим о натуральных и целых числах. Но что именно они обозначают? Какие основные понятия связаны с этими числами и какие характеристики они имеют? В данном разделе мы рассмотрим основные определения и свойства натуральных и целых чисел, а также их различия и взаимосвязь.
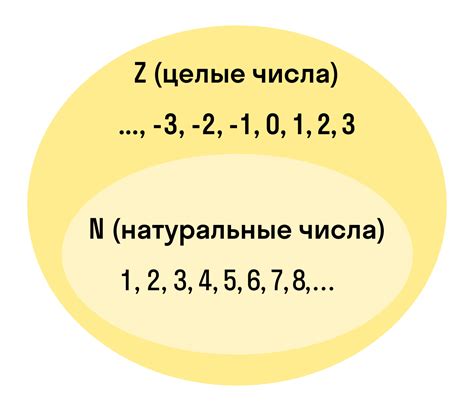
Натуральные числа представляют собой знаки, обозначающие количество или порядок предметов или явлений в нашем окружающем мире. Они включают в себя числа, начиная с единицы и продолжаясь бесконечно вправо по числовой оси. Натуральные числа используются для подсчета, упорядочивания и классификации объектов.
Примеры натуральных чисел: 1, 2, 3, 4, 5, 6, и так далее.
Целые числа включают в себя не только натуральные числа, но и отрицательные числа, а также ноль. Они обозначают как количество предметов или явлений, так и их отсутствие или отрицательное значение. Целые числа служат инструментом для измерения разницы между двумя значениями, обозначения долгов, температуры и многих других величин.
Примеры целых чисел: -3, -2, -1, 0, 1, 2, 3, и так далее.
Одно из главных различий между натуральными и целыми числами заключается в наличии или отсутствии нуля и отрицательных значений. Эти числовые системы обладают своими особенностями и свойствами, которые будут рассмотрены в данной статье. Понимание и использование натуральных и целых чисел является важным для решения различных задач из разных областей знания, от математики до ежедневных расчетов.
Содержание натуральных чисел и их применение в математике

Представьте себе мир математики, где есть числа, отражающие количество и порядок, без упоминания о целых или дробных числах. В этом разделе мы рассмотрим понятие натуральных чисел и способы их использования в различных математических операциях.
Натуральные числа - это числа, которые обозначают количество объектов или их порядковый номер в упорядоченной последовательности. Как правило, они начинаются с единицы и обозначаются символом "N". Натуральные числа широко применяются в различных областях математики, включая алгебру, геометрию, теорию вероятностей и другие.
Одним из основных применений натуральных чисел является подсчет объектов в группах или множествах. Например, если у вас есть 5 яблок и вы добавляете еще 3 яблока, то общее количество яблок составит 8. Здесь натуральные числа использовались для подсчета количества объектов и представления результатов.
Натуральные числа также могут использоваться для указания порядка и ранжирования объектов. Например, если вам нужно расположить фотографии в альбоме, вы можете нумеровать их с помощью натуральных чисел. Когда вы сортируете фотографии, вы используете порядок натуральных чисел для определения их места в последовательности.
Более сложные математические операции, такие как сложение, вычитание, умножение и деление, также могут быть выполнены с использованием натуральных чисел. Например, если у вас есть 3 яблока и вы хотите добавить еще 2 яблока, то результатом будет 5 яблок. Аналогично, если у вас есть 6 конфет и вы разделите их на 2 группы, каждая группа будет содержать 3 конфеты.
| Математическая операция | Пример | Результат |
|---|---|---|
| Сложение | 3 + 2 | 5 |
| Вычитание | 7 - 4 | 3 |
| Умножение | 4 x 5 | 20 |
| Деление | 12 ÷ 3 | 4 |
Разнообразие типов и применение целых чисел в практике

Одним из наиболее распространенных видов целых чисел являются позитивные целые числа, которые представляют положительные числа без дробной части. Их можно встретить во множестве аспектов нашей повседневной жизни, например, во время вычислений, связанных с количеством предметов или людей.
Еще одним важным типом целых чисел являются отрицательные целые числа. Они представляют отрицательные числовые значения без дробной части. Такие числа могут быть полезными при расчетах, связанных с долгами, температурными показателями или отрицательными значениями силы.
Кроме того, существуют нулевое целое число, которое используется в различных сценариях. Ноль является особым числом, которое может выполнять роль нейтрального элемента в определенных математических операциях или служить началом отсчета в определенных системах координат.
Применение целых чисел в практике демонстрирует их ценность и значимость. От финансистов и ученых до разработчиков программного обеспечения и инженеров - все они используют целые числа, чтобы решать реальные задачи и облегчать свою работу. Понимание типов целых чисел и возможность применять их грамотно становится все более важным навыком в современном мире.
Уникальные особенности и отличия между положительными целыми числами и числами, обозначающими количество предметов или явлений

Когда мы говорим о целых числах и числах, характеризующих количество предметов или явлений, мы сталкиваемся с различными особенностями и спецификой. Несмотря на то, что оба типа чисел относятся к разделу математики, они имеют свои уникальные свойства и правила, которыми следует руководствоваться при их использовании.
- В основе натуральных чисел лежит идея о количестве предметов, явлений или людей. Эти числа непосредственно связаны с реальными объектами и служат для их подсчета или измерения. Натуральные числа – это основа для формирования понятия о количестве и последовательности событий, а также помогают осуществлять сравнение и классификацию.
- Целые числа, в свою очередь, шире охватывают спектр возможных значений. Они могут быть как положительными, так и отрицательными, а также включают нуль, который служит отметкой принадлежности к данному числовому множеству. Целые числа имеют свои уникальные правила сложения, вычитания, умножения и деления, которые отличаются от тех, которые используются при работе с натуральными числами.
- Еще одной важной особенностью целых чисел является возможность их использования в арифметических операциях с переменными и константами. Они позволяют строить сложные математические выражения, вычислять значения функций и моделировать различные явления и процессы.
- Важно отметить, что при работе с натуральными числами мы имеем дело с ограниченным множеством значений, тогда как целые числа предоставляют нам гораздо большую свободу при выборе численного диапазона. Целые числа также шире используются в научных и общественных исследованиях, где требуется точность и степень детализации.
В итоге, хотя целые числа и числа, обозначающие количество предметов или явлений, имеют некоторые общие черты, они все же представляют собой различные аспекты и подходы к работе с числами. Обладая своими уникальными свойствами и правилами, эти числа выполняют важные функции в нашей повседневной жизни и в научной области.
Особенности целых чисел и натуральных чисел
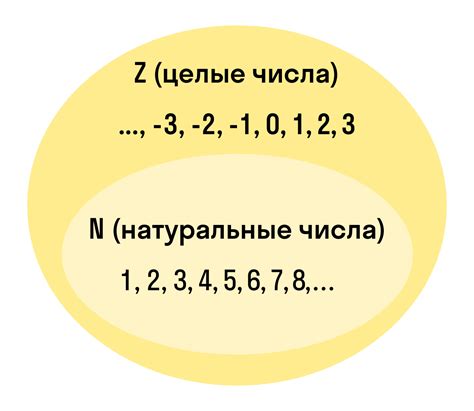
Натуральные числа, также известные как положительные целые числа, представляют собой набор чисел, которые появились первоначально в связи с естественными процессами и счетом. Они обычно используются для подсчета объектов или установления последовательности событий. Натуральные числа обозначаются символами, которые приходят нам на ум, когда мы думаем о нумерации: 1, 2, 3, и так далее.
С другой стороны, целые числа включают в себя набор натуральных чисел, а также отрицательные числа и ноль. Они могут использоваться для измерения температуры ниже нуля или для подсчета долга. Целые числа помечаются используя знаки «-» (минус) и «+» (плюс), а также цифры, которые отображают конкретные значения.
Помимо этих различий в определении и диапазоне чисел, целые числа и натуральные числа обладают разными математическими свойствами. Натуральные числа являются бесконечными, в то время как целые числа включают в себя конечные и бесконечные. Оба типа чисел также имеют свои уникальные правила для операций сложения, вычитания, умножения и деления.
| Натуральные числа | Целые числа |
|---|---|
| 1, 2, 3, 4, ... | ..., -3, -2, -1, 0, 1, 2, 3, ... |
Итак, понимание различий между целыми числами и натуральными числами позволяет нам использовать их в подходящем контексте и применять правильные математические операции для достижения желаемых результатов.
Вопрос-ответ

В чем основное различие между целыми и натуральными числами?
Основное различие между целыми и натуральными числами заключается в их множествах. Натуральные числа состоят из всех положительных целых чисел, начиная с единицы и не имеют нуля и отрицательных чисел. Целые числа, в свою очередь, включают в себя натуральные числа, а также ноль и все отрицательные числа.
Зачем нужны целые и натуральные числа в математике?
Целые и натуральные числа играют важную роль в математике. Натуральные числа используются для подсчета, измерения количества и указания порядка. Они широко применяются в различных областях науки, физике, экономике и технике. Целые числа расширяют понятие натуральных чисел, позволяя учитывать отрицательные значения и ноль. Они применяются для моделирования долгов, температур, координат и других понятий, где важно учитывать направление и отношение между числами.
Какие правила работы с целыми числами существуют?
Правила работы с целыми числами включают основные свойства сложения, вычитания, умножения и деления. Например, сложение двух положительных чисел даёт положительный результат, а сложение чисел с разными знаками осуществляется с вычитанием модулей. Правила также относятся к умножению и делению, где важно учитывать знаки чисел. Эти правила облегчают работу с целыми числами и позволяют получать корректные результаты при выполнении математических операций.
Как описать различия между целыми и натуральными числами в обыденной жизни?
Различия между целыми и натуральными числами можно привести в примерах из обыденной жизни. Натуральные числа могут использоваться для подсчета количества предметов, например, количество яблок в корзине. Целые числа дополняют понятие натуральных чисел, позволяют учитывать задолженности и температурные отклонения. Например, если у вас на счету 100 рублей, то это натуральное число, а если у вас -50 рублей, то это целое отрицательное число.



