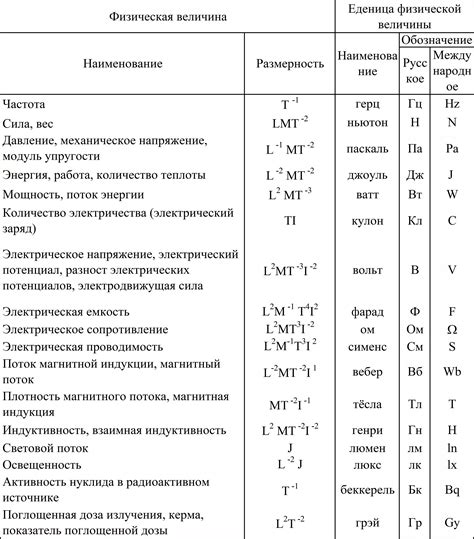
Физика, как наука, изучает различные виды явлений и процессов, которые возникают в природе. Для того чтобы описывать их, физики используют различные определенные понятия и меры, одним из которых является измерение физических величин. В процессе измерений выделяют два основных типа величин: скалярные (числовые) и векторные.
Скалярные величины представляют собой численные характеристики, которые не требуют определенной направленности или ориентации в пространстве для своего описания. Они могут иметь только значение, которое может быть положительным, отрицательным или нулевым. Примерами скалярных величин могут служить: масса, объем, температура, длина и время. Эти величины характеризуются только числовыми значениями и не имеют направления.
Векторные величины, в свою очередь, имеют более сложную структуру, так как они не только численно характеризуют явления и процессы в физике, но и обладают определенным направлением. Для полного описания векторной величины необходимо указать как ее значение, так и направление, в котором она действует. Например, скорость, ускорение, сила и сила тяжести являются векторными величинами, так как они характеризуются численным значением и направлением.
Описание и особенности векторных физических величин

Особенностью векторных физических величин является то, что они описывают перемещения, силы и другие физические явления в пространстве. Например, векторная величина скорости указывает не только на величину перемещения, но и на направление движения. Это позволяет более точно описывать движение тела и предсказывать его будущее положение.
- Векторные физические величины могут быть представлены в виде стрелки, которая указывает на их направление. Длина стрелки соответствует числовому значению величины.
- Векторные величины могут складываться и вычитаться друг из друга. При сложении векторов учитывается как их числовое значение, так и направление.
- Векторные величины обладают свойством ориентированности. Это значит, что вектор может быть направлен как в положительном, так и в отрицательном направлении, в зависимости от выбранной системы координат.
- Векторная величина может быть разложена на две или более компоненты по различным направлениям. Это позволяет более детально анализировать физические явления и проводить более точные расчеты.
Таким образом, векторные физические величины представляют собой специальный вид величин, обладающих не только числовым значением, но и направлением. Они позволяют более точно описывать и анализировать физические явления в пространстве.
Сущность векторных величин

В мире физики существуют особые величины, которые обладают особенными свойствами и дополнительными характеристиками по сравнению с простыми числовыми величинами. Эти величины называются векторными физическими размерами. В отличие от скалярных величин, которые полностью определяются своим числовым значением, векторные величины несут у себя дополнительную информацию о направлении и силе.
Векторные физические величины - это уникальные объекты, которые помимо значения в численном формате имеют важные характеристики, такие как направление и ориентация. Это значит, что эти величины не могут быть полностью описаны только числовой информацией. Единица измерения векторной величины несет не только скалярную характеристику, но и векторное значение, описывающее направление и интенсивность физического явления.
Наличие направления и величины необходимо для полного описания векторной физической величины. Такие величины могут быть представлены в виде стрелок с определенным направлением и длиной, графически. Например, скорость, сила, ускорение и момент силы являются примерами векторных физических величин, которые требуют дополнительной информации для полного описания своей природы.
Векторные физические величины играют важную роль в физике, так как они помогают не только оценить значение, но и предоставляют информацию о направлении и магнитуде физического явления. Понимание этих величин помогает изучать и анализировать такие явления, как движение, деформация, взаимодействия тел и другие процессы, которые требуют учета направления и силы воздействия.
В итоге, векторные физические величины представляют собой специальный вид измерений, описывающий значения не только числовыми данными, но и дополнительными характеристиками, такими как направление и интенсивность. Их понимание и использование способствует более точному анализу и объяснению физических явлений в нашем мире.
Основные характеристики векторных величин

В данном разделе мы рассмотрим основные характеристики, которые отличают векторные величины от скалярных. Когда мы говорим о векторах, мы имеем дело с физическими величинами, которые не только обладают числовым значением, но также имеют направление и могут быть представлены графически.
Первой характеристикой векторных величин является их направление. В отличие от скалярных величин, векторы имеют определенную ориентацию в пространстве. Это означает, что вектор можно представить в виде стрелки, указывающей на определенное направление. Например, вектор скорости в механике может указывать на направление движения объекта.
Второй характеристикой векторных величин является их величина. Как и в случае со скалярами, векторы также имеют численное значение, которое может быть измерено. Однако, векторная величина также учитывает длину стрелки, обозначающей вектор. Иными словами, чем длиннее стрелка, тем больше величина вектора. Например, вектор силы может быть более сильным, если его стрелка длиннее.
Третьей характеристикой, свойственной векторным величинам, является их коммутативность. Векторы могут быть перемещены в пространстве без изменения результатов. Например, если мы имеем два вектора скорости, их сложение будет давать тот же результат, независимо от их порядка. Это свойство отличает векторы от скалярных величин, для которых порядок может влиять на результат.
Таким образом, основные характеристики векторных величин включают их направление, величину и коммутативность. Эти свойства делают векторы полезными инструментами для описания физических процессов и отличают их от скалярных величин, которые не обладают такими характеристиками.
| Характеристика | Описание |
|---|---|
| Направление | Векторы имеют определенное ориентированное направление в пространстве. |
| Величина | Векторы имеют числовое значение, а также учитываются их длины. |
| Коммутативность | Векторы можно переместить в пространстве без изменения результатов. |
Определение и особенности алгебраических величин в физике- Одной из особенностей алгебраических величин является то, что они могут быть представлены в виде чисел без привязки к какому-либо направлению. Например, время, масса, температура – все эти величины являются алгебраическими и характеризуются только числовыми значениями.
- Другой особенностью алгебраических величин является то, что их значения могут быть складываны и вычитаны. Например, если у нас есть две алгебраические величины – масса тела и ее скорость, мы можем сложить их значения, чтобы получить импульс. Это позволяет нам производить различные математические операции и моделировать физические процессы.
- Еще одним аспектом алгебраических величин является их отсутствие направления. Такие величины нельзя представить в виде стрелки или указать на них определенное направление, что отличает их от векторных величин.
- Большинство алгебраических величин можно измерить с помощью определенных единиц измерения, таких как метры, килограммы, секунды и т.д. Это позволяет стандартизировать и сравнивать значения различных алгебраических величин.

В целом, алгебраические величины являются основой для математического описания физических явлений и широко используются в физике. Понимание и усвоение особенностей алгебраических величин является важным шагом для понимания физических принципов и законов.
Понятие скалярных физических величин: основные характеристики и свойства

В научной дисциплине, изучающей природу и явления окружающего мира, используются многообразные физические величины. Некоторые из них имеют особый характер и представлены в виде векторов, а другие описываются скалярными величинами. Определение и понимание скалярных физических величин необходимы для формирования базовых концепций физики и их применения в различных научных и технических областях.
Скалярные физические величины являются важным аспектом изучения природы и взаимодействия объектов. Они отражают такие основные характеристики явлений и процессов, как масса, объем, плотность, температура, время и многое другое. Отличительной чертой скалярных величин является их способность быть полностью описанными числами, лишенными направления и ориентации в пространстве. В отличие от векторных величин, которые имеют не только величину, но и направление, скалярные величины характеризуются только числовыми значениями, присущими им самостоятельно.
- Скалярные физические величины не зависят от выбранной системы координат и не изменяются при повороте осей система отсчета.
- Операции сложения и вычитания применимы к скалярам, и результат этих операций опять будет скаляром.
- Умножение скаляра на скаляр или вектор также дает скалярный результат.
- Скалярные величины могут быть сравнены между собой с помощью операций "больше", "меньше" или "равно".
- Измерение скалярных величин происходит с использованием единиц измерения, которые определены в соответствии с международными стандартами.
В итоге, скалярные физические величины представляют собой фундаментальные концепции физики, которые используются для описания и измерения различных состояний и свойств объектов. Понимание их основных характеристик и свойств является необходимым для глубокого и точного анализа различных физических явлений, а также для разработки научных и технических решений, связанных с изучением мира вокруг нас.
Уникальная природа скалярных физических величин
Когда речь заходит о физических величинах, мы всегда сталкиваемся с двумя основными типами: векторными и скалярными. В нашей статье мы уже изучили особенности векторных физических величин, теперь пришло время обратить внимание на те аспекты, которые делают скаляры такими уникальными.
Скаляры - это физические величины, которые полностью определяются только числовыми значениями, без всякой информации о направлении или ориентации. Это означает, что они лишены стрелок, векторных диаграмм или координатных осей. В отличие от векторов, скаляры не имеют направленной природы, они лишь характеризуются числовыми значениями.
Одной из ключевых особенностей скалярных величин является то, что они могут быть просто складываемы или вычитаемы друг из друга. В отличие от векторов, где необходимо учитывать направление и расстояние, скаляры позволяют производить арифметические операции без дополнительных сложностей. Например, если у нас есть две скалярные величины - масса и объем, мы можем легко сложить их вместе, чтобы получить общую массу или объем.
Скалярные физические величины также могут быть представлены в виде числовых значений с определенными единицами измерения, что делает их более понятными и удобными в использовании. Это позволяет нам измерять такие параметры, как время, длина, площадь, температура и многие другие, используя стандартные единицы и проводить сравнения или вычисления на основе этих числовых значений.
| Примеры скалярных величин | Примеры векторных величин |
|---|---|
| Масса | Сила |
| Время | Скорость |
| Температура | Ускорение |
Интерпретация направленности векторных величин

Направленность векторных величин в физике имеет большое значение, так как она позволяет нам описывать движение, силы, магнитные поля и многие другие физические явления. Каждому вектору можно сопоставить определенное направление, которое может быть задано, например, геометрически или в виде угла относительно определенной оси.
Интерпретация направленности векторных величин позволяет нам легко определять их взаимное положение и влияние друг на друга. Например, векторное произведение двух векторов может нам показать, будет ли результирующая сила параллельна другому вектору или направлена перпендикулярно к нему.
Уникальная способность векторных величин интерпретировать направленность делает их незаменимыми инструментами в физике, инженерии, аэродинамике и многих других областях. Без учета направленности векторных величин мы не смогли бы полноценно описывать мир вокруг нас и предсказывать различные физические явления.
Влияние направленности векторных величин на их физическую природу
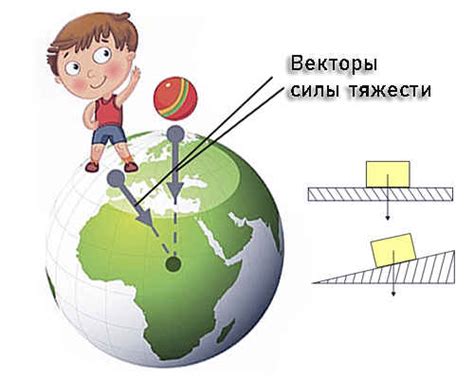
Направление вектора определяет ориентацию и силу его воздействия. Как стрелка на компасе указывает на север, направленность вектора указывает на конкретное направление физического явления или движения. Эта особенность позволяет точно определить, каким образом величина влияет на окружающую среду и какой эффект она производит.
Например, векторная величина скорости не только указывает на величину движения объекта, но и указывает на его направление. Это позволяет понять, куда смещается объект и каким образом он будет взаимодействовать с другими объектами или силами. Направленность вектора также играет важную роль при работе с векторной суммой, которая позволяет сложить или разложить векторы для анализа их взаимодействия. Без учета направленности, результаты вычислений и прогнозов могут быть неправильными или неполнотой представлять собой реальность.
Таким образом, понимание и учет направленности векторных физических величин является неотъемлемой частью их характеристики. Направленность позволяет определить ориентацию силы или физического явления, предсказать его взаимодействие с окружающей средой и точно описать его эффекты. Без учета направленности, понимание физического мира было бы значительно ограничено, и многие явления оставались бы необъяснимыми.
Вопрос-ответ

Чем отличаются векторные физические величины от скалярных?
Векторные физические величины отличаются от скалярных тем, что они имеют не только величину, но и направление. Скалярные величины, напротив, характеризуются только величиной и не имеют направления.
Как можно определить, является ли физическая величина векторной или скалярной?
Для определения характера физической величины необходимо учесть, есть ли у нее только величина или одновременно величина и направление. Если величина имеет только численное значение, то она является скалярной. Если же помимо численного значения имеется также указание на направление, то величина является векторной.
Какое простое объяснение можно дать разнице между векторными и скалярными величинами?
Простым объяснением разницы между векторными и скалярными величинами может служить следующий пример: представьте, что нашей задачей является описание перемещения объекта. Если нам достаточно знать только величину перемещения без указания направления, то мы используем скалярную величину. Однако, если нам важно указать не только величину перемещения, но и направление, то мы используем векторную величину.
Какие примеры можно привести в качестве векторных физических величин?
Примеры векторных физических величин: сила, скорость, ускорение, импульс, момент силы. Все эти величины имеют численное значение, а также направление, которое указывает, в какую сторону действует величина.
Какие примеры можно привести в качестве скалярных физических величин?
Примеры скалярных физических величин: масса, время, длина, энергия, температура. Эти величины характеризуются только числовым значением и не имеют направления.



