Когда речь заходит о физических явлениях, величины играют первостепенную роль в описании и изучении природы. Но что делает одну величину отличной от другой? Действительно, различия между разными видами физических величин могут быть существенными и определяющими в их применении и понимании. Некоторые из таких различий можно обнаружить в роде ориентированности и направленности величин, которые могут принимать на себя.
Ориентированные физические величины - это те, которые имеют не только численное значение, но и определенное направление. Проще говоря, они указывают на конкретную точку в пространстве, с прикрепленным к ней вектором, который определяет его величину и направление. Подобные величины, например, можно встретить в случае изучения движения тела, где скорость и ускорение представляют собой векторные величины, указывающие на направление и величину изменения положения объекта.
В свою очередь, безнаправленные физические величины лишены векторных свойств и могут быть представлены только числовыми значениями. Такие величины часто обозначаются термином "скалярные". К примеру, масса, объем или температура - все это хорошие примеры скалярных величин. В отличие от векторных величин, скаляры не зависят от направления и указывают только на величину данного явления. Таким образом, они не обладают стрелкой или вектором, указывающим на определенную точку в пространстве.
Понятие векторов и скаляров в физике

В физике существует различие между двумя типами физических величин: векторными и скалярными.
Векторы являются величинами, которые имеют как численное значение, так и направление. Они представляют собой стрелки, указывающие на определенную точку в пространстве. Направление вектора определяет, куда он указывает, а его длина представляет собой величину этого вектора. Например, сила, скорость и ускорение - это векторные величины.
Скаляры, в свою очередь, представляют собой величины, обладающие только численными значениями без какого-либо определенного направления. Они могут быть положительными, отрицательными или нулевыми, и обычно измеряются в единицах измерения, таких как масса, время, температура и объем.
Отличительной особенностью векторных величин является то, что они могут быть сложены и вычитаны друг из друга, а также могут быть умножены на число. Например, две силы могут быть сложены, чтобы получить общую силу, или векторное умножение может использоваться для определения момента силы. Скаляры, напротив, могут быть только сложены или умножены на число.
В общем, различие между векторными и скалярными величинами в физике определяется наличием или отсутствием направления у величины. Это позволяет проводить более детальные и точные анализы физических явлений и событий, а также использовать математические операции для получения новых значений и характеристик.
Векторные атрибуты в физике: понятия и особенности

В мире физики существует особая категория величин, которые отличаются от обычных скалярных атрибутов своими специфическими свойствами, называемыми векторами. Векторы имеют определенные направления и величины, которые существенно влияют на их физическое поведение и взаимодействие с окружающей средой.
Векторные величины представляют собой математическую абстракцию, которая обладает несколькими характеристиками. Во-первых, они имеют направление, которое задается в пространстве. Отклонения от этого направления могут существенно изменить значения этих векторов. Направление может быть выражено, например, в виде точки или вектора, указывающего на конкретное место в пространстве.
| Особенности векторных величин | |
|---|---|
| Направление | Задается в пространстве и влияет на поведение вектора. |
| Величина | Измеряется величиной, которая указывает на силу или мощность вектора. |
| Сложение | Векторы могут быть сложены или вычитаны для получения нового вектора. |
| Умножение | Векторы могут быть умножены на скаляры для изменения их величины. |
| Результат | Результат сложения или умножения векторов также будет вектором. |
Сложение векторов осуществляется путем соединения их начал и концов. Полученный вектор, называемый результатом векторного сложения, будет иметь направление и величину, определяемые исходными векторами.
Умножение вектора на число, или скаляр, изменяет его величину, но не направление. Усиление или ослабление векторных свойств может быть достигнуто с помощью умножения на соответствующий коэффициент.
Скалярные величины

Скалярные величины могут быть представлены числами без указания направления или ориентации. Они описываются только одним параметром, который может иметь определенное значение. Например, масса, время, плотность, температура и скорость - все эти величины являются скалярными.
Для скалярных величин не требуется указывать их направление и положение в пространстве. Они характеризуются только численным значением, что часто упрощает математические расчеты и анализ физических процессов.
Однако, несмотря на то что скалярные величины не обладают направлением, они могут иметь важную информацию о физическом явлении. Например, знание массы тела позволяет определить его инерцию, а знание температуры газа - его энергетическое состояние.
Скалярные величины играют важную роль в физике, так как позволяют описывать и измерять основные свойства и характеристики объектов и явлений, не учитывая их направление и ориентацию в пространстве.
Представление векторов и скаляров
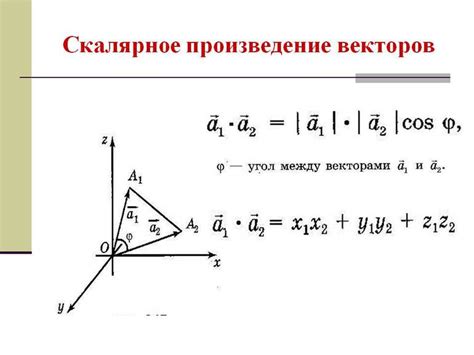
В данном разделе будет рассмотрено как векторные и скалярные физические величины представлены в нашем понимании и влияют на изучение мира природы.
Векторы и скаляры – это различные способы измерения и описания физических явлений и объектов.
Векторные величины, как правило, имеют такие характеристики, как направление и модуль. Они описываются вектором и могут быть представлены в виде стрелки, указывающей направление величины, а длина стрелки показывает модуль этой величины.
Скалярные величины, в свою очередь, описываются только модулем и не имеют направления. Они являются простыми числами и часто отражают различные физические величины, такие как время, масса или температура.
Понимание различий между векторными и скалярными величинами очень важно для построения математических моделей и решения задач в физике и других науках. Это позволяет более точно описывать и предсказывать поведение и взаимодействие объектов в пространстве и времени.
Геометрическое отображение направленных векторов
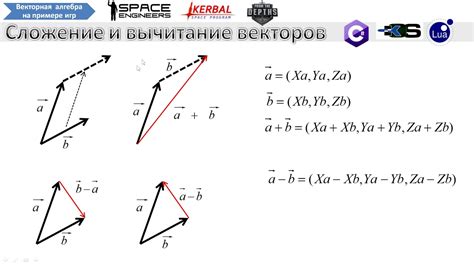
Если мы рассматриваем векторные физические величины, то для их полного описания необходимо указать не только их численное значение, но и направление. Геометрическое представление векторов помогает визуализировать их направление и учитывать это свойство при выполнении математических операций или анализе физических процессов.
В отличие от скалярных величин, которые характеризуются только численным значением и не имеют направления, векторы представляют собой направленные отрезки прямых линий. Направление вектора может быть указано стрелками, линиями или другими геометрическими фигурами, которые визуально указывают на его ориентацию в пространстве.
Один из способов геометрического представления векторов - использование координатной системы. В этом случае, каждый вектор определяется величиной и направлением, представленными числами или углами относительно координатных осей. Такое представление помогает наглядно показать, как два вектора связаны друг с другом и как изменение одного вектора влияет на другие величины или физические процессы.
Геометрическое отображение векторов не только упрощает понимание связей между различными физическими величинами, но и позволяет визуально предсказывать результаты операций с векторами или анализировать физические явления в контексте их направления. Направленность векторов играет значительную роль во многих областях физики и инженерии, и геометрическое представление векторов - важная составляющая в изучении их свойств и применении в реальных задачах.
Вопрос-ответ

Какая основная разница между векторными и скалярными физическими величинами?
Основная разница между векторными и скалярными физическими величинами заключается в том, что векторные величины имеют направление и величину, тогда как скалярные величины имеют только величину, но не имеют направления.
Какие примеры можно привести в качестве векторных физических величин?
Примерами векторных физических величин являются сила, скорость, ускорение, импульс, момент силы, векторы магнитной и электрической индукции и множество других.
Какие примеры можно привести в качестве скалярных физических величин?
Примерами скалярных физических величин являются масса, время, температура, объем, плотность, работа, энергия и множество других величин, которые характеризуются только числовыми значениями без направления.
Каким образом можно определить направление векторной физической величины?
Направление векторной физической величины можно определить с помощью направления вектора или с помощью использования координатных осей, где положительное направление указывает на направление вектора, а отрицательное - в противоположном направлении.
Какие математические операции можно выполнять с векторными физическими величинами?
С векторными физическими величинами можно выполнять операции сложения, вычитания, умножения на скаляр, вычисления векторного произведения и скалярного произведения. Эти операции позволяют учесть как направление, так и величину векторных величин при их взаимодействии и расчетах.



