Существует множество фигур, которые нас окружают в повседневной жизни. Однако, не все из них обладают такой же геометрической структурой. Определить, является ли данная фигура параллелограммом, имеет большое значение в различных сферах: от строительства до графики, от геодезии до архитектуры. Так как определить на первый взгляд параллелограмм на основе его внешних признаков не всегда возможно, существуют определенные правила и методы его распознавания.
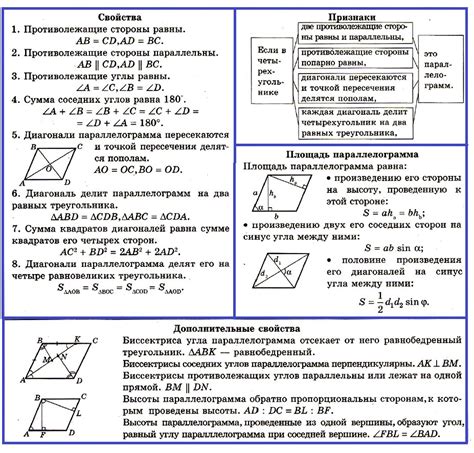
Параллелограмм – это геометрическая фигура, определяющаяся чередованием параллельных сторон. Он представляет собой четырехугольник, в котором противоположные стороны параллельны и равны между собой. Кроме того, параллелограмм обладает некоторыми особыми особенностями, которые позволяют более уверенно подтвердить его природу.
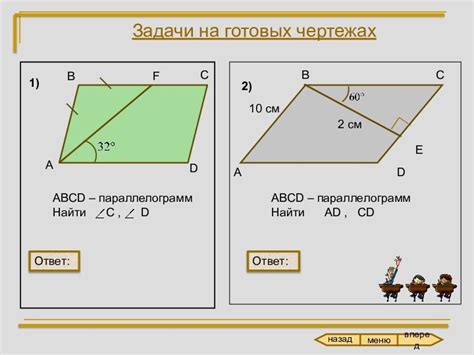
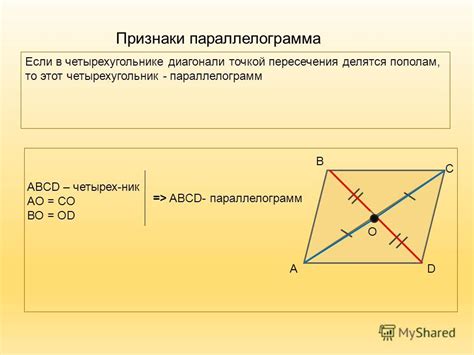
Для того чтобы узнать, что фигура является параллелограммом, необходимо обратить внимание на такие признаки, как: соответствующие стороны должны быть равны друг другу и параллельны; противоположные углы должны быть равны; диагонали должны делиться пополам. Если все эти критерии выполняются, то можно с уверенностью утверждать, что фигура – параллелограмм.
Особенности геометрической фигуры с параллельными сторонами
Прежде всего, важно отметить, что параллелограмм является четырехугольником, у которого противоположные стороны параллельны друг другу. Такое свойство делает его особенно интересным и полезным для различных математических операций и задач. Однако, это не единственный признак параллелограмма. Для его полного определения и доказательства параллельности сторон в фигуре, следует рассмотреть и другие свойства.
Второй важный признак параллелограмма связан с его углами. Внутренние углы параллелограмма всегда равны между собой, а сумма любых двух смежных углов противоположных сторон также составляет 180 градусов. Это характерное свойство является отличительным признаком и помогает установить параллельность сторон в данной фигуре.
Также, одним из признаков параллелограмма является равенство диагоналей. Диагонали параллелограмма делят его на два равных треугольника и взаимно делятся пополам. Это равенство является дополнительным фактором, свидетельствующим о параллельности противоположных сторон.
Наконец, прямая, соединяющая середины двух противоположных сторон, всегда является параллельной двум другим противоположным сторонам. Это последний признак параллелограмма, который подчеркивает его геометрическую устойчивость и связь между сторонами.
Таким образом, изучение этих основных признаков параллелограмма дает возможность более глубокого понимания и использования этой геометрической фигуры в различных математических и практических задачах.
Основные характеристики фигуры
Чтобы фигура могла называться параллелограммом, необходимо, чтобы все его стороны были параллельны. Более того, каждая пара противоположно расположенных сторон должна быть одинаковой длины. Основываясь на этих принципах, можно построить доказательство параллельности сторон в данной фигуре.
- Параллельные стороны олицетворяют собой две прямые линии, которые никогда не пересекаются, будучи расположенными в одной плоскости.
- Параллелограмм имеет четыре угла, противоположные стороны которых сходятся под прямыми углами. Выполнение данного требования также является неотъемлемой характеристикой параллелограмма.
- Противоположные стороны параллелограмма равны по длине, что подразумевает их параллельность.
- Каждый угол параллелограмма составляет смежный угол с противоположным углом, их сумма всегда равна 180 градусам.
Исходя из вышеуказанных характеристик параллелограмма, становится возможным доказать параллельность сторон данной фигуры и восстановить геометрическую пропорциональность.
Углы в параллелограмме: свойства и особенности
В данном разделе мы рассмотрим основные характеристики углов в параллелограмме. Углы в данной фигуре играют важную роль и обладают определенными свойствами, которые позволяют нам классифицировать и анализировать данную геометрическую форму. Понимание этих свойств поможет нам более глубоко исследовать и понять параллелограммы в их различных вариациях.
В параллелограмме существуют три основных типа углов: вершиная, противоположные и смежные углы. Вершина параллелограмма – это точка пересечения двух сторон. Вершиные углы представляют собой углы, образованные этими сторонами и гранями, смежными с ними. Противоположные углы в параллелограмме находятся на противоположных углах фигуры и равны между собой. Смежные углы – это пары углов, расположенных рядом с противоположными углами параллелограмма.
В общем, углы в параллелограмме представляют собой ключевые элементы, которые помогают нам исследовать и анализировать эту фигуру в контексте ее структуры и особенностей. Понимание основных свойств и характеристик углов позволяет нам более глубоко погрузиться в изучение параллелограммов и определить их признаки и особенности без необходимости использования конкретных определений.
Стороны и диагонали в четырехугольнике с параллельными сторонами
Стороны параллелограмма обладают рядом уникальных особенностей. Во-первых, они имеют одинаковую длину и параллельны друг другу. Это означает, что напротив каждой стороны есть параллельная сторона с такой же длиной. Благодаря этому свойству параллелограмм можно удобно классифицировать и изучать его геометрические свойства.
Диагонали параллелограмма также играют важную роль. Во-первых, они делят фигуру на два треугольника. При этом, диагонали в параллелограмме равны между собой, что делает эту фигуру особым образом симметричной. Кроме того, одну из диагоналей можно рассматривать как вектор, соединяющий противоположные вершины параллелограмма, что открывает новые возможности для вычисления различных параметров фигуры.
Таким образом, изучение сторон и диагоналей параллелограмма позволяет нам лучше понимать его форму и свойства. Это является важным шагом для дальнейшего анализа и применения данной фигуры в геометрии и других областях науки.
| Свойство | Объяснение |
|---|---|
| Строны | Равны по длине и параллельны друг другу |
| Диагонали | Равны между собой и делят фигуру на два треугольника |
Доказательство параллельности линий в четырехугольнике ABCD
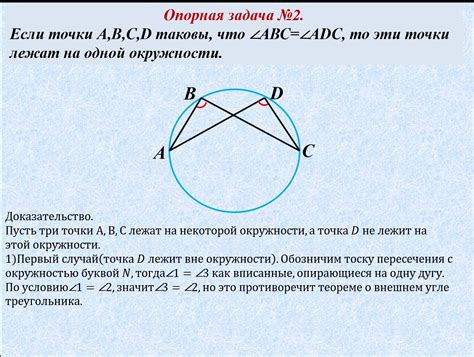
В данном разделе мы рассмотрим методы и приемы, которые позволяют доказать параллельность сторон в четырехугольнике ABCD. Будут представлены несколько ключевых идей, которые помогут нам строить логическую цепочку рассуждений для подтверждения данного утверждения.
Для начала, мы обратимся к существованию пары параллельных сторон в четырехугольнике. Важно понимать, что параллельные линии имеют одинаковый наклон и никогда не пересекаются. Отсюда следует, что если в четырехугольнике имеются две параллельные стороны, то все остальные стороны также должны быть параллельны.
Кроме того, важным фактом является равенство соответствующих углов при параллельных сторонах. Если углы между параллельными сторонами одинаковы, то стороны также являются параллельными. Это правило можно применять как в случае параллелограмма, так и в других четырехугольниках.
Свойства многогранных фигур
1. Параллельность сторон
Мы узнаем, какие условия позволяют нам утверждать, что стороны фигуры параллельны. Некоторые из этих свойств связаны с углами или длинами сторон, а другие - с отношениями между сторонами и диагоналями. Мы изучим эти свойства и узнаем, как использовать их для определения параллельности сторон.
2. Симметрия и равенство сторон
Будет рассмотрено, как симметричность геометрических фигур связана с их свойствами. Мы узнаем о параллелограммах с равными сторонами и какой тип симметрии они обладают. Также будут рассмотрены случаи, когда стороны параллелограмма равны между собой. Мы изучим, как использовать эти свойства для определения различных классов параллелограммов.
3. Отношения между сторонами и углами
В этом разделе мы изучим, как связаны стороны и углы параллелограмма. Будут рассмотрены различные формулы и теоремы, которые позволяют нам выражать отношения между сторонами и углами с помощью числовых и математических выражений. Мы узнаем, как использовать эти отношения для доказательства свойств параллелограмма.
Свидетельства сонаправленности отрезков AB и CD

Процесс установления параллельности AD и BC

Понятие параллельности сторон в геометрии необходимо для определения формы многоугольника и его свойств. В данном разделе мы изучим процесс установления параллельности отрезков AD и BC и его доказательство.
Для начала, мы рассмотрим характерные признаки, которые указывают на параллельность данных отрезков. Отметим основные критерии, среди которых совпадение углов между отрезками, равенство соответствующих углов, равенство противоположных сторон и другие свойства, которые помогут нам понять, являются ли данные отрезки параллельными.
Для того чтобы строить доказательство параллельности отрезков AD и BC у фигуры, необходимо использовать первоначальные данные о расположении этих отрезков и их взаимодействии с другими элементами фигуры. Мы применим метод построения параллельных отрезков с использованием вспомогательных прямых и углов, что позволит нам логически и убедительно доказать, что данные отрезки являются параллельными.
Установление параллельности AD и BC имеет важное значение при исследовании свойств различных геометрических фигур и решении задач, связанных с построением и измерением. Грамотное и точное доказательство параллельности сторон фигуры позволяет нам более глубоко изучать ее характеристики и проявления в геометрической плоскости.
Вопрос-ответ

Какие признаки указывают на то, что фигура является параллелограммом?
Есть несколько признаков, по которым можно установить, является ли данная фигура параллелограммом. Во-первых, внутренние углы параллелограмма должны быть равными. Во-вторых, противоположные стороны параллелограмма должны быть равными и параллельными. В-третьих, диагонали параллелограмма должны делиться пополам и пересекаться в точке, которая является центром симметрии фигуры.
Как можно доказать, что стороны фигуры ABCD параллельны?
Для доказательства параллельности сторон в фигуре ABCD можно использовать разные методы. Один из способов - это сравнение углов. Если углы между соответствующими сторонами фигуры равны, то это указывает на их параллельность. Другой метод - это использование свойств перпендикуляров и параллельных линий. Если стороны фигуры выстраиваются таким образом, что передние и задние ребра соответственно параллельны, то стороны также являются параллельными. Также, можно использовать доказательство от противного - предположить, что стороны не являются параллельными, и показать, почему это противоречит другим свойствам фигуры.
Можно ли установить параллельность сторон фигуры ABCD без использования углов?
Да, можно установить параллельность сторон фигуры ABCD, не используя углы. Один из методов - это использование равенства отрезков. Если отрезки, соответствующие сторонам фигуры, равны друг другу, то это указывает на их параллельность. Также, можно использовать свойства симметрии. Если фигура ABCD имеет ось симметрии, то стороны, которые перпендикулярны этой оси, также являются параллельными. Кроме того, можно использовать свойства параллельных линий. Если стороны фигуры пересекаются с параллельной линией, то они также являются параллельными.



