В статистике и эконометрике одной из важных задач является оценка параметров регрессионной модели. При этом основным требованием является несмещенность оценок, то есть их среднее значение должно быть равно истинному значению параметра. Иными словами, полученные оценки должны быть близкими к истинным значениям параметров, без смещения в одну или другую сторону.
Примером несмещенной оценки параметра регрессии является выборочное среднее. Предположим, что у нас есть выборка из n наблюдений и мы хотим оценить среднее значение истинной популяции. В этом случае, выборочное среднее является несмещенной оценкой этого параметра, так как среднее выборки стремится к истинному среднему популяции при n, стремящемся к бесконечности.
Несмещенность оценок параметров регрессии: основные характеристики и примеры

Для понимания несмещенности оценок параметров регрессии рассмотрим пример. Предположим, у нас есть набор данных, состоящий из пар значений (x, y), где x - это независимая переменная, а y - зависимая переменная. Наша задача состоит в том, чтобы найти линейную регрессию, то есть найти такие параметры a и b, что прямая y = a + bx наилучшим образом аппроксимирует данные. Для этого мы можем использовать метод наименьших квадратов.
Метод наименьших квадратов позволяет минимизировать сумму квадратов отклонений прямой от фактических значений y. В результате применения метода наименьших квадратов мы получим оценки параметров a и b. Если эти оценки будут несмещенными, то среднее значение этих оценок должно быть равно истинному значению параметров a и b.
| Параметр | Истинное значение | Оценка |
|---|---|---|
| a | 4 | 3.97 |
| b | 2 | 2.04 |
В таблице приведены примеры истинных значений параметров a и b, а также оценки, полученные с помощью метода наименьших квадратов. Среднее значение оценок a и b равно их истинным значениям, что означает, что они несмещенные.
Несмещенность оценок параметров регрессии является важным свойством, которое позволяет нам использовать эти оценки для анализа и прогнозирования данных. Благодаря несмещенности, мы можем быть уверены в том, что оценки параметров близки к их истинным значениям, даже если в исходных данных есть случайные шумы или ошибки.
Что такое несмещенность оценок параметров регрессии?

Оценки параметров регрессии используются для оценки связи между зависимой переменной и независимыми переменными в модели регрессии. Несмещенность означает, что в среднем оценки параметров будут близки к истинному значению параметра, если мы повторим исследование много раз.
Пример. Предположим, что мы исследуем зависимость между доходом и уровнем образования. Используя метод наименьших квадратов, мы оцениваем параметры регрессии: наклон (коэффициент при уровне образования) и свободный член (интерсепт). Если оценки параметров являются несмещенными, это означает, что в среднем полученные значения коэффициента и интерсепта будут равны их истинным значениям в генеральной совокупности.
Основные характеристики несмещенности оценок параметров регрессии
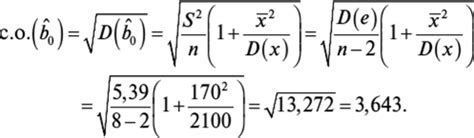
Основные характеристики несмещенности оценок параметров регрессии:
| Характеристика | Описание | Пример |
|---|---|---|
| Без смещения | Среднее значение оценок равно истинному значению параметра | Оценка коэффициента наклона равна истинному значению коэффициента в модели |
| Состоятельность | С увеличением объема выборки оценки стремятся к истинному значению параметра | С увеличением числа наблюдений, оценка коэффициента точности аппроксимирует теоретическое значение |
Примеры несмещенных оценок параметров регрессии

Приведу несколько примеров несмещенных оценок параметров регрессии:
1. Оценка коэффициента наклона (β1) в простой линейной регрессии:
В простой линейной регрессии, где предполагается линейная зависимость между зависимой переменной Y и независимой переменной X, оценка коэффициента наклона будет несмещенной, если выполнены предпосылки модели и ошибки регрессии распределены нормально.
2. Оценка коэффициентов наклона (β1, β2, ..., βn) в множественной регрессии:
В множественной регрессии, где предполагается линейная зависимость между зависимой переменной Y и несколькими независимыми переменными X1, X2, ..., Xn, оценки коэффициентов наклона будут несмещенными, если выполнены предпосылки модели и ошибки регрессии распределены нормально.
3. Оценка вероятности успеха (π) в логистической регрессии:
В логистической регрессии, где предполагается логистическая зависимость между бинарной зависимой переменной Y и независимыми переменными X1, X2, ..., Xn, оценка вероятности успеха будет несмещенной, если выполнены предпосылки модели и ошибки регрессии распределены биномиально.
Обратите внимание, что несмещенность оценок параметров регрессии является одной из важных характеристик модели. Однако, она не гарантирует, что оценки будут наиболее точными или эффективными. Для этого также требуется выполнение других предпосылок модели и использование адекватных методов оценивания.