Когда мы обращаемся к математике, часто сталкиваемся с задачей нахождения значения функции. Это вопрос, который может вызывать затруднение для многих, особенно для тех, кто только начинает изучать эту науку. Но не стоит паниковать! Существуют простые и эффективные подходы, которые помогут нам найти искомое значение без лишней сложности и запутанности.
Один из таких подходов основан на использовании алгебраических операций и свойств функций. Мы можем применять арифметические операции (сложение, вычитание, умножение, деление) и использовать свойства функций (ассоциативность, коммутативность, дистрибутивность), чтобы упростить задачу и выразить значение функции через известные нам параметры и операции.
Другим полезным инструментом является анализ графика функции. Мы можем найти значения функции, опираясь на ее графическое представление. Для этого мы должны знать основные особенности графика, такие как точки перегиба, экстремумы, асимптоты и интервалы монотонности. Анализируя эти факторы, мы можем определить, в какой области функции находится искомое значение и приближенно его искать или точно определить его значение.
Решение функциональных выражений в заданной точке
В данном разделе будем рассматривать методы вычисления значения математических функций в конкретных точках. Можно использовать различные подходы и алгоритмы, позволяющие получить результат, исходя из входных данных и заданных условий.
Для подсчета значения функции в заданной точке, можно использовать основные математические операции и арифметические операторы, такие как сложение, вычитание, умножение и деление. Также при вычислении могут применяться такие операции, как возведение в степень, извлечение корня, модуль числа и т.д.
Для того чтобы найти значение функции, следует использовать свойства и законы, связанные с данной функцией. Например, для тригонометрических функций можно использовать тригонометрические тождества, а для логарифмических функций - свойства логарифмов.
Однако, при использовании вычислительных методов следует быть внимательным и учитывать ограничения и условия, которые могут влиять на результат. Например, некоторые функции могут быть не определены в некоторых точках, что может привести к ошибкам или неоднозначным результатам.
Графическое изображение результатов функции
Визуальный подход к определению значений функции позволяет с помощью графиков и диаграмм наглядно представить зависимость переменных и получить представление о значениях функции в различных точках. Этот метод оказывается полезным при решении задач и анализе данных, когда требуется быстро оценить результаты функции без непосредственных расчетов.
Аналитическое нахождение значения функции
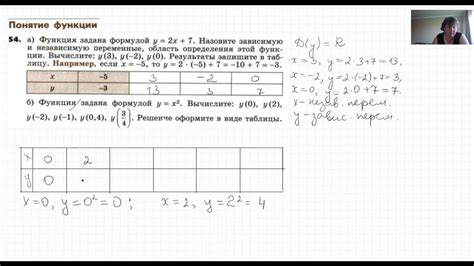
В данном разделе рассмотрим методы, позволяющие определить значение функции без необходимости использования численных методов или графических представлений.
При аналитическом нахождении значения функции, учитываются синонимы такие как решение, определение, вычисление, предсказание и т.д. аналитикой.
| Метод | Описание |
|---|---|
| Подстановка | Метод, при котором значение независимой переменной заменяется вместо ее символического обозначения. После подстановки выражения в функцию сокращаются и упрощаются для получения значения функции. |
| Раскрытие скобок | Метод, основанный на упрощении выражений путем раскрытия скобок. Этот подход позволяет привести выражение к более простому виду для последующего вычисления значения функции. |
| Алгебраические преобразования | Метод, использующий правила алгебры для манипулирования выражениями и приведения их к более простому виду. Это позволяет упростить выражение и найти значение функции. |
| Формулы и тождества | Метод, при котором используются известные формулы и тождества для перехода от исходного выражения к более простым и понятным выражениям. Это позволяет вычислить значение функции. |
Аналитическое нахождение значения функции является важным инструментом, который помогает упростить вычисления и понять свойства функции без необходимости использования сложных численных методов.
Использование таблиц и графиков для определения значения функции
В данном разделе представлена возможность использования таблиц и графиков для определения точного значения функции. Этот метод позволяет упростить процесс вычислений и визуально представить результаты.
С помощью таблицы можно представить значения функции для определенного диапазона переменных. Разбивая интервал значений на равные отрезки и вычисляя значение функции для каждого из них, можно создать таблицу, которая отражает зависимость между переменной и функцией. Такая таблица часто называется таблицей значений.
График функции позволяет наглядно представить ее поведение в зависимости от переменной. Строя график, можно увидеть, как меняется значение функции в разных точках диапазона переменных. Кривая графика отображает закономерности и особенности функции, что облегчает нахождение ее значения в определенной точке.
Таким образом, использование таблиц и графиков является удобным методом для определения значения функции, позволяющим визуализировать зависимость между переменной и функцией. Этот подход помогает с легкостью найти точное значение функции в любой заданной точке и упростить процесс вычислений.
Использование математических операций для вычисления значений функций
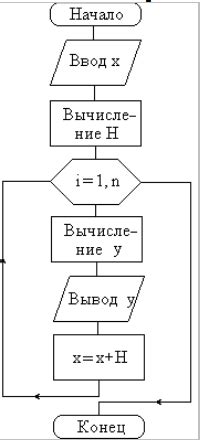
Этот раздел статьи посвящен методам применения математических операций в процессе нахождения значений функций. В математике существует множество разнообразных способов подсчета значений функций, которые могут использоваться в различных контекстах и задачах. В данном разделе мы рассмотрим некоторые из этих методов, сосредоточиваясь на простых и эффективных подходах.
Чтобы находить значения функций, мы можем использовать различные математические операции, такие как сложение, вычитание, умножение и деление. Более сложные операции, такие как возведение в степень, извлечение корня, логарифмирование, также могут быть полезны в определенных случаях. Каждая из этих операций дает нам возможность преобразовать аргументы функций и получить их значения.
Важно понимать, что выбор подходящих математических операций для нахождения значений функций зависит от свойств и параметров конкретной функции. Некоторые функции могут быть выражены через простые арифметические операции, например, линейные функции, поэтому для их вычисления может потребоваться только базовый набор операций. Другие функции могут требовать применения более сложных операций, таких как экспоненциальная функция или тригонометрические функции.
Наиболее эффективный подход к использованию математических операций для нахождения значений функций состоит в анализе свойств и паттернов функций, а также в выборе наиболее подходящих операций для решения конкретных задач. С использованием правильных операций и методов, мы можем упростить вычисления и получить нужные значения функций с минимальными усилиями. В следующих разделах мы более детально рассмотрим применение различных математических операций для нахождения значений функций в различных контекстах.
Вопрос-ответ

Какие есть простые способы нахождения значения функции?
Есть несколько простых способов для нахождения значения функции. Первый способ - это подстановка значения аргумента в формулу функции. Например, если у нас есть функция f(x) = 2x + 3, и нам нужно найти значение функции при x = 4, мы просто подставляем это значение в формулу: f(4) = 2 * 4 + 3 = 11. Еще один способ - это построение графика функции и нахождение значения функции в нужной точке путем считывания значений на графике. Если у нас есть функция f(x) = x^2, и нам нужно найти значение функции при x = 2, мы строим график функции, и видим, что значение функции в точке x = 2 равно 4.
Какая формула используется для нахождения значения функции?
Формула для нахождения значения функции зависит от конкретной функции. Для многих функций можно использовать простую алгебраическую формулу, в которую подставляются значения аргументов. Например, если у нас есть функция f(x) = 3x - 2, формула для нахождения значения функции будет f(x) = 3 * x - 2. Мы просто подставляем значение аргумента в формулу и получаем результат. Для других функций, таких как тригонометрические функции или экспоненциальные функции, могут использоваться специальные формулы, которые учитывают особенности этих функций.
Можно ли найти значение функции без использования формулы?
Да, можно найти значение функции без использования формулы, например, путем построения графика функции. Для этого нужно построить график функции на координатной плоскости и считать значение функции в нужной точке. Если у нас есть функция f(x) = x^2, и нам нужно найти значение функции при x = 2, мы строим график функции, и видим, что значение функции в точке x = 2 равно 4.
Есть ли другие способы, помимо подстановки и графика, для нахождения значения функции?
Да, помимо подстановки значения аргумента и использования графика, есть и другие способы для нахождения значения функции. Один из них - использование таблицы значений функции. Мы создаем таблицу, где указываем значения аргумента и считаем значения функции при каждом значении аргумента. Например, для функции f(x) = 2x + 3, мы можем создать таблицу, где в первом столбце указываем значения x, а во втором столбце считаем значения функции f(x). Другой способ - это использование специальных свойств функций, таких как симметрия или периодичность. Зная эти свойства функции, можно найти значения функции без прямого вычисления.
Какие простые способы существуют для нахождения значения функции?
Существует несколько простых способов для нахождения значения функции. Один из них - подстановка значений входных переменных в выражение функции и вычисление получившегося выражения. Другой способ - использование графика функции, где значение функции найдется путем определения координаты на оси ординат в соответствии с заданной координатой на оси абсцисс.



