Все мы знаем, что математика окружает нас повсюду: в нашей повседневной жизни, на работе, в наших увлечениях. И одной из самых фундаментальных и важных областей математики является арифметика. Понимание основных закономерностей и правил арифметики позволяет нам анализировать и работать с числами. Одним из таких важных понятий является степень. Степени возникают в различных математических задачах и имеют свои особенности, одна из которых - степень двойки.
В данном разделе мы рассмотрим, как определить, является ли число степенью двойки. Хотя это может показаться сложным и запутанным вопросом, на самом деле есть несколько простых правил и приемов, которые помогут нам легко и быстро распознать, кратно ли число двум.
Окей, давайте разберемся, что такое степень двойки. Степенью двойки называется число, которое получается путем нескольких последовательных умножений двойки саму на себя. Например, 2 в первой степени равно 2, 2 во второй степени равно 4, 2 в третьей степени равно 8 и так далее. Таким образом, степень двойки представляет собой числовой ряд, где каждое следующее число получается умножением предыдущего на два.
Определение чисел, являющихся степенью двух: основная информация

Одним из ключевых признаков чисел, которые являются степенями двойки, является их бинарное представление. Такие числа всегда имеют только одну единицу в двоичной записи и все остальные цифры являются нулями. Важно отметить, что двоичное представление числа, являющегося степенью двойки, всегда начинается с единицы, а затем следуют только нули.
Кроме того, существуют алгоритмы проверки чисел на степень двойки. Один из таких алгоритмов основан на использовании операции побитового И (&), которая позволяет проверить, являются ли все разряды числа нулями, кроме самого старшего разряда, который должен быть равен единице.
- Проверка бинарного представления числа.
- Использование операции побитового И (&).
Эти методы позволяют определить, является ли число степенью двойки или нет и могут быть полезны в различных областях, таких как программирование, теория алгоритмов и криптография.
Что такое степень двойки и почему она имеет важность?

Существует определенное свойство чисел, называемое степенью двойки, которое играет важную роль в различных областях науки и техники. Математические понятия, основанные на степенях двойки, встречаются повсеместно и имеют множество приложений.
- Одно из главных свойств степени двойки заключается в том, что это число, возведенное в определенную степень, всегда будет являться степенью двойки. Например, число 2 в квадрате равно 4, а число 2 в кубе равно 8.
- Степени двойки широко применяются в компьютерной науке и информатике. Из-за того, что компьютеры используют двоичную систему счисления, степени двойки представляют собой ключевые элементы в хранении данных и выполнении арифметических операций.
- Степени двойки также играют важную роль в теории вероятностей и статистике. Например, степенной анализ используется для определения вероятности наступления событий и расчета различных статистических показателей.
- В электронике и цифровой технике степени двойки встречаются в виде значений сопротивлений, емкостей и других характеристик элементов схемы. Использование степеней двойки облегчает процесс расчетов и проектирования.
- Определение чисел, являющихся степенями двойки, может быть полезным при работе с большими наборами данных или при разработке эффективных алгоритмов. Знание, что число имеет степень двойки, позволяет оптимизировать процессы и упрощает работу с числами.
Итак, степени двойки - это определенное свойство чисел, которое позволяет использовать их в различных областях науки и техники. Знание о степени двойки и ее применении помогает в решении разнообразных задач и оптимизации процессов, что делает это понятие важным и полезным.
Легкий метод проверки, является ли число кратным двум

Особенности степеней двойки в двоичной системе
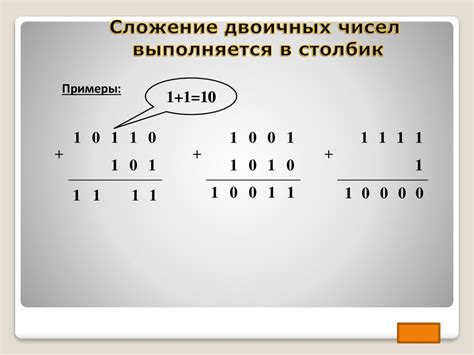
Уникальность степеней двойки в двоичной системе
Степени двойки являются особым классом чисел в двоичной системе счисления. Они обладают рядом уникальных свойств, которые делают их особенными и удобными для использования в различных сферах.
Степени двойки и единственность представления
Одной из особенностей степеней двойки в двоичной системе является их способность представляться единственным образом. Каждая степень двойки имеет уникальное двоичное представление, что позволяет легко идентифицировать и распознавать эти числа.
Степени двойки и побитовые операции
Побитовые операции, такие как сдвиг влево и сдвиг вправо, активно используются при работе со степенями двойки в двоичной системе. Это позволяет выполнять быстрые и эффективные вычисления, основанные на свойствах степеней двойки.
Степени двойки и алгоритмы
Степени двойки также находят применение в различных алгоритмах, используемых в программировании и информатике. Их использование может значительно ускорять вычисления и оптимизировать процессы, связанные с работой со множеством данных.
Степени двойки и битовая арифметика
Битовая арифметика – важный аспект работы со степенями двойки в двоичной системе. Благодаря своей уникальной структуре и представлению, степени двойки могут обрабатываться особым образом, что позволяет выполнять различные операции над ними с высокой эффективностью.
Рекурсивная проверка числа на соответствие степени числа двойки
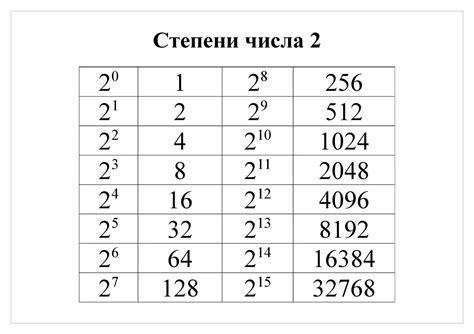
Алгоритм начинает с того, что проверяет, делится ли число на 2 без остатка. Если число делится на 2, а затем проверяется, является ли результат деления степенью двойки. Если да, то число считается степенью двойки, иначе алгоритм продолжает проверку с новым значением, полученным в результате деления на 2.
Если число не делится на 2 без остатка, то оно не может быть степенью двойки и алгоритм возвращает ложное значение.
Рекурсивное решение позволяет просто и эффективно проверить, является ли число степенью числа двойки, не требуя сложных вычислений и итераций. Оно может быть полезным при различных задачах, включая оптимизацию и анализ данных.
Использование побитовых операций для определения степени двойки
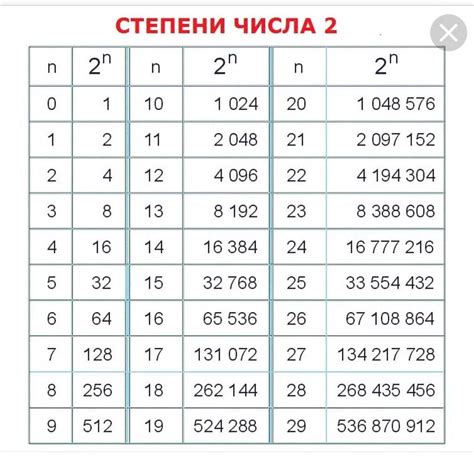
Одна из наиболее часто используемых побитовых операций - это побитовое И (&), которое выполняет операцию "И" между двумя битами. Если результат этой операции равен нулю, то все биты числа, кроме одного, равны нулю, что говорит о том, что число является степенью двойки.
Для определения степени двойки необходимо проверить, равен ли результат побитового И между числом и числом минус один нулю. Если это условие выполняется, то число является степенью двойки.
С помощью побитовых операций можно определить степень двойки в эффективной и наглядной манере, применяя логические операции над битами числа. Это может быть полезно, например, при разработке алгоритмов или при работе с двоичным представлением чисел.
Математические характеристики степеней двойки и их применение

Одним из наиболее распространенных признаков является бинарное представление чисел. Если число представляется только набором единиц и нулей, то оно, скорее всего, является степенью двойки. Например, число 4 в двоичной системе будет выглядеть как 100, а число 8 – 1000. Преимущество данного признака в его быстроте и простоте использования при анализе больших числовых последовательностей.
Другим полезным математическим признаком является связь между степенью двойки и делением числа на 2. Если при повторном делении числа на 2 результаты оказываются целыми числами, то данное число является степенью двойки. Например, число 16 делится на 2 без остатка два раза: 16 ÷ 2 = 8, 8 ÷ 2 = 4.
Кроме того, существует математическое правило, позволяющее определить, является ли число степенью двойки с помощью операции побитового сравнения. Для этого необходимо выполнить побитовое И числа n и n-1. Если результат равен нулю, то число является степенью двойки. Например, для числа 16 выполнение операции 16 & (16-1) = 16 & 15 = 0 подтверждает, что оно является степенью двойки.
Математические признаки степеней двойки широко используются в программировании для оптимизации алгоритмов и структур данных. Они позволяют эффективно работать с большими объемами данных, а также упрощают реализацию некоторых алгоритмов и операций. Например, в компьютерной графике и обработке изображений используется степени двойки для оптимизации размеров и размещения текстурных и пиксельных данных.
- Бинарное представление чисел: простой и быстрый признак степени двойки.
- Повторное деление на 2: проверка чисел на степень двойки.
- Побитовое сравнение и операция И: точный способ определить степень двойки.
- Применение в программировании и технологиях: оптимизация алгоритмов и структур данных.
Вопрос-ответ

Как определить, является ли число степенью двойки?
Для определения того, является ли число степенью двойки, нужно проверить, делится ли оно на два без остатка. Если число делится на два без остатка, значит, оно является степенью двойки. Если же число не делится на два без остатка, то оно не является степенью двойки.
Какие числа являются степенями двойки?
Числа, которые являются степенями двойки, представляют собой результат умножения двойки на себя несколько раз. Например, числа 2, 4, 8, 16, 32 и так далее являются степенями двойки. Они получаются путем умножения двойки на двойку несколько раз: 2*2=4, 2*2*2=8, 2*2*2*2=16 и так далее.
Как определить, сколько раз нужно умножить двойку, чтобы получить данное число?
Чтобы определить, сколько раз нужно умножить двойку, чтобы получить данное число, можно воспользоваться логарифмами. Необходимо найти логарифм данного числа по основанию два. Найденное значение будет показывать, сколько раз нужно умножить двойку, чтобы получить данное число. Например, если логарифм числа 16 по основанию два равен 4, это значит, что число 16 получается путем умножения двойки на двойку четыре раза: 2*2*2*2=16.



