Откройте для себя новый метод, который позволит вам легко и точно определить расположение вершин гиперболы!
Гиперболы – загадочные и изящные математические объекты, встречающиеся во многих сферах науки и техники. Они обладают уникальной формой, отличной от привычных кругов и эллипсов. Хотя гиперболы могут показаться сложными для анализа, существует простой и эффективный способ найти их вершины, который доступен каждому из нас.
Секрет заключается в использовании математических принципов, которые на первый взгляд могут показаться сложными, но на самом деле они легко усвоятся благодаря правильному подходу. Разделение этого метода на несколько простых шагов позволит вам не только легко найти вершины гиперболы, но и понять, как это делается.
Этот способ не требует специальных навыков или математического образования – он подходит как для начинающих, так и для опытных исследователей и любителей. Проведите свое личное математическое исследование и откройте для себя мир гиперболических кривых!
Понятие гиперболы и ее вершины

В данном разделе рассмотрим основные аспекты понятия гиперболы и ее вершин, важные для понимания и изучения данной геометрической фигуры.
- Общая характеристика гиперболы
- Определение вершин гиперболы
- Свойства и связь вершин с остальными частями гиперболы
Гипербола – это одно из базовых понятий геометрии, которое широко используется в различных областях науки и техники. Гипербола представляет собой кривую линию, которая обладает определенными математическими свойствами. Она состоит из двух отдельных, симметричных ветвей, которые расходятся в бесконечности.
Вершины гиперболы являются одним из важных элементов в ее структуре и определении. Вершины – это точки пересечения осей симметрии гиперболы и ее ветвей, где кривая касается осей координат. Они обладают определенными свойствами и играют ключевую роль в анализе и построении гиперболы.
Вершины гиперболы определяют ее форму и размеры. Они служат главными точками для проведения осей симметрии и построения ее главных элементов, таких как вертикальные и горизонтальные асимптоты. Вершины также обладают свойством отражаться относительно фокусов гиперболы.
Таким образом, понятие гиперболы и ее вершин является важным элементом в изучении геометрических фигур и их свойств. Понимание основных характеристик и связи с остальными элементами позволяет более глубоко изучать и использовать гиперболы в разных областях знания.
Структура гиперболы и особенности ее краевых точек
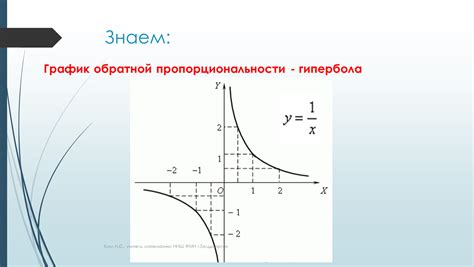
Этот раздел посвящен рассмотрению структуры гиперболы и ключевым особенностям ее краевых точек. Мы изучим способы определения их координат, а также роль, которую они играют в геометрии данной кривой.
Чтобы полностью понять структуру гиперболы, необходимо разобраться в определении вершин и их связи с другими элементами. Нужно обратить внимание на то, что вершины гиперболы представляют собой точки пересечения кривой с осями координат. Они имеют особое значение, так как определяют базовые параметры графика гиперболы и ее направление. Кроме того, вершины позволяют определить центр гиперболы и провести оси симметрии.
Рассмотрим основные характеристики вершин гиперболы. Обратите внимание, что у каждой гиперболы может быть две пары вершин, три точки из которых лежат на главной оси, а одна - на лирической. Каждая пара вершин имеет свои уникальные координаты, определяющие положение гиперболы на плоскости. Изучение этих координат позволяет получить информацию о внешнем виде гиперболы и ее геометрическом расположении относительно осей координат.
Таким образом, раздел "Структура гиперболы и особенности ее краевых точек" позволяет более детально изучить важные характеристики вершин данной геометрической фигуры. Понимание и анализ координат вершин гиперболы являются ключевыми для построения графиков, анализа и решения геометрических задач, связанных с этой кривой.
Методологии и стратегии обнаружения расположения экстремальных точек гиперболы
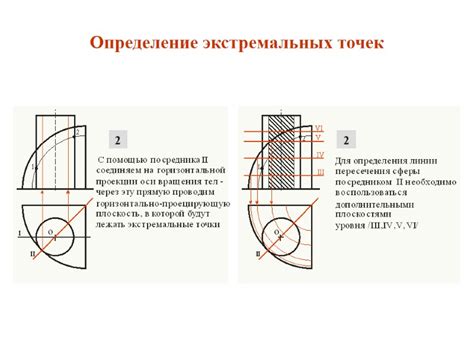
В данном разделе мы рассмотрим различные методы и алгоритмы, которые находят применение при проведении исследований вершин гиперболы. Здесь мы представим разнообразные подходы и стратегии, которые помогут исследователям обнаружить и определить расположение экстремальных точек гиперболической кривой без особых трудностей.
Первый из таких методов - метод аналитического подхода. С его помощью, исследователь проводит дифференцирование исходной уравнения гиперболы, используя свойства производных для определения точек, в которых реализуется экстремум гиперболической кривой. В этом случае, рассматриваются уравнения первого и второго порядков, что позволяет выявить расположение вершин гиперболы.
Другой подход, который может быть применен в процессе поиска вершин гиперболы, - это наблюдательный метод. Здесь исследователь использует специальные тестовые точки, для которых происходит вычисление значений функции и ее производных. Следующим шагом является анализ полученных данных для определения, являются ли эти точки экстремумами гиперболической кривой или нет.
Кроме того, существуют методы, основанные на численном решении задачи поиска. Используя итерационные алгоритмы и численные методы, исследователи могут эффективно находить вершины гиперболы и изучать их свойства. Здесь используется последовательное приближение и определение момента, когда достигается экстремальная точка гиперболической кривой.
- Метод аналитического подхода
- Наблюдательный метод
- Методы численного решения
Каждый из этих методов имеет свои преимущества и недостатки. Выбор конкретной стратегии зависит от ситуации и задач, стоящих перед исследователем. Комбинирование различных подходов может привести к более точным результатам и более полному пониманию геометрических характеристик гиперболической кривой.
Геометрический подход к определению осей симметрии гиперболы

В данном разделе мы рассмотрим геометрический метод для определения вершин гиперболы, используя основные принципы ее структуры.
Гипербола - это особый вид кривой в геометрии, которая имеет две ветви и является симметричной относительно центральной оси. Наше задание состоит в том, чтобы найти точки на оси, в которых гипербола достигает своих самых удаленных точек от центральной оси. Эти точки называются вершинами гиперболы.
Предлагается использовать геометрический подход, использующий свойство гиперболы, что расстояние от каждой точки гиперболы до центра равно разности расстояний между этой точкой и двумя фокусами гиперболы. Особым свойством гиперболы является то, что этот дифференциал расстояния на самом деле является постоянным - полуразностью фокусных расстояний.
Используя данное свойство и определение гиперболы, мы можем разработать алгоритм для поиска вершин гиперболы, основанный на геометрическом подходе. Начальные шаги включают построение координатной плоскости и определение координат центра гиперболы. Затем, используя экспериментальные данные, мы можем находить полуразность фокусных расстояний и, следовательно, точки на центральной оси, где расстояние до гиперболы достигает своего максимума.
Геометрический способ нахождения вершин гиперболы позволяет нам понять и визуализировать основные концепции и свойства этой кривой, что делает его полезным инструментом для изучения и понимания гиперболических функций и уравнений.
Геометрический подход к определению характеристик гиперболы

В данном разделе мы рассмотрим геометрический подход к определению ключевых характеристик гиперболы: фокусных расстояний и полуосей. Вместо использования сложных математических формул и вычислений, мы предлагаем простой метод, основанный на графическом представлении гиперболы и ее свойствах.
Для начала, рассмотрим само понятие гиперболы и ее основные геометрические свойства. Гипербола - это плоская кривая, обладающая двумя фокусами и постоянной разностью расстояний до точек на кривой. Важно отметить, что гипербола имеет две ветви, которые симметрично расположены относительно центра симметрии - центра гиперболы.
Для определения фокусных расстояний и полуосей, необходимо провести некоторые геометрические построения и использовать свойства гиперболы. Для начала, построим фокусную точку F1 и произвольную точку P1 на гиперболе.
Затем, проведем перпендикуляр к оси симметрии, проходящий через точку P1, и продлим его до пересечения с другой ветвью гиперболы - точкой P2. Заметим, что расстояние от F1 до точки P2 будет равно расстоянию от F1 до точки P1.
Следующим шагом является построение основных элементов гиперболы - фокусных расстояний и полуосей. Фокусное расстояние можно определить как расстояние от центра гиперболы до любой фокусной точки, например, от центра до F1. Полуось - это расстояние от центра гиперболы до одной из вершин, например, от центра до P1.
Повторив эти построения для второй ветви гиперболы, мы получим вторую фокусную точку F2 и вторую вершину P3. Таким образом, геометрическим подходом мы можем определить фокусные расстояния и полуоси гиперболы без использования сложных уравнений и вычислений.
Искомые точки гиперболы при заданных параметрах
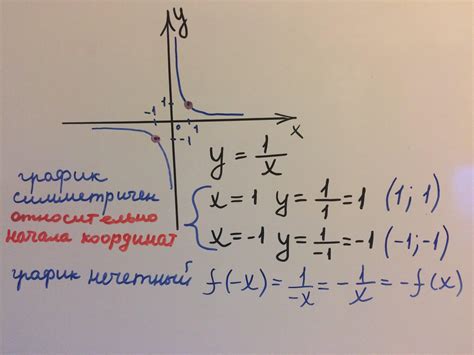
Раздел посвящен решению задачи определения вершин гиперболы в соответствии с определенными условиями. Приведены алгоритмы, позволяющие легко определить координаты вершин гиперболы без необходимости проведения сложных вычислений или использования специальных программных инструментов.
Алгебраический метод определения фокусов гиперболы

Для начала рассмотрим уравнение гиперболы, заданное в общей форме. Оно содержит две переменных и является второй степени. Для определения фокусов гиперболы необходимо найти коэффициенты, отвечающие за положение фокусов по осям координат.
Для этого воспользуемся методикой приведения уравнения гиперболы к каноническому виду. Путем подбора коэффициентов и дальнейшего алгебраического преобразования уравнения, мы сможем выразить положения фокусов гиперболы в явном виде. Значения координат фокусов будут зависеть от конкретных параметров гиперболы, таких как фокусное расстояние и направление открытия.
Полученные результаты позволят нам точно определить вершины гиперболы и изучить ее пространственные свойства. Алгебраический метод, описанный в данном разделе, является надежным и универсальным инструментом для анализа гиперболических функций, как в теоретической математике, так и в практических приложениях.
Алгебраический подход к выявлению экстремальных точек гиперболы

В данном разделе будет рассмотрено алгебраическое решение задачи поиска вершин гиперболы. Вместо использования геометрических методов и конкретных определений, мы сосредоточимся на алгебраической обработке уравнений и систем для определения этих точек.
Предлагается использовать дифференциальные уравнения, аналитическую геометрию и матричные вычисления для нахождения координат экстремальных точек гиперболы. Применение алгебраического подхода позволяет упростить процесс нахождения вершин и получить точные значения.
- Во-первых, необходимо определить параметры гиперболы, такие как фокусное расстояние и полуоси.
- Затем используя уравнение гиперболы с найденными параметрами, составляется система уравнений для определения координат экстремальных точек.
- Далее, путем решения системы уравнений методами алгебры и матричного анализа, получаем точные значения координат вершин гиперболы.
Алгебраический подход к поиску вершин гиперболы позволяет осуществлять точные расчеты без использования сложных геометрических конструкций. Этот метод обладает высокой точностью и применим ко множеству видов гипербол. Он является эффективным и удобным инструментом для математического анализа и решения соответствующих геометрических задач.
Примеры решения задач с применением алгебраического подхода

Этот раздел демонстрирует использование алгебраического метода для решения различных задач. Алгебраический подход позволяет найти вершины гиперболы и определить ее основные параметры. Ниже приведены примеры решения задач с использованием данного метода.
| Пример 1 | Пример 2 | Пример 3 |
|---|---|---|
| Решение задачи о поиске вершин гиперболы с заданными уравнениями и координатами точек. | Определение осей симметрии и фокусов гиперболы при заданных параметрах. | Нахождение уравнения гиперболы по заданным характеристикам и координатам точек. |
| Алгоритм решения: | Алгоритм решения: | Алгоритм решения: |
| 1. Записать уравнение гиперболы в стандартной форме. | 1. Определить значения a и b в уравнении гиперболы. | 1. Используя уравнение гиперболы и данные о точках, составить систему уравнений. |
| 2. Сравнить коэффициенты у уравнения гиперболы с формулами для нахождения вершин. | 2. Найти оси симметрии и фокусы по полученным значениям a и b. | 2. Решить систему уравнений, используя методы алгебры, и получить уравнение гиперболы. |
| 3. Подставить найденные значения в уравнение гиперболы и получить координаты вершин. | 3. Проверить полученные значения геометрически. | 3. Проверить полученное уравнение, подставив координаты точек и проверив их совпадение. |
Вопрос-ответ

Как найти вершины гиперболы?
Для поиска вершин гиперболы нужно найти центр гиперболы и затем определить полуоси. Вершины будут находиться на пересечении гиперболы с осями координат.
Как найти центр гиперболы?
Для поиска центра гиперболы нужно определить, где пересекаются оси координат. Это будут координаты центра гиперболы.
Как найти полуоси гиперболы?
Для определения полуосей гиперболы нужно найти расстояние от центра до вершин гиперболы. Полуоси будут представлять это расстояние.
Как использовать найденные вершины гиперболы?
Вершины гиперболы позволяют определить основные параметры гиперболы, такие как фокусные расстояния и эксцентриситет. Они также могут быть использованы для построения графика гиперболы.
Есть ли более сложные способы нахождения вершин гиперболы?
Да, существуют и более сложные способы нахождения вершин гиперболы, например, с использованием математических выкладок или геометрических построений. Однако, описанный в статье метод является более простым и доступным для понимания.
Как можно легко найти вершины гиперболы?
Для нахождения вершин гиперболы можно использовать несколько простых способов. Один из них – использование уравнения гиперболы в их координатах. Для гиперболы с уравнением вида (x - h)^2 / a^2 - (y - k)^2 / b^2 = 1, вершины будут находиться в точках с координатами (h ± a, k).
Есть ли альтернативные способы для поиска вершин гиперболы?
Да, существует несколько альтернативных способов для нахождения вершин гиперболы. Один из них – использование геометрического определения гиперболы, которое заключается в том, что гипербола – это множество точек, для каждой из которых абсолютное значение разности расстояний до двух фиксированных точек (фокусов) одинаково. Нахождение вершин в этом случае можно выполнить, построив перпендикуляры к оси симметрии гиперболы из фокусов и находя точки их пересечения с кривой.



