В нашей повседневной жизни мы часто сталкиваемся с необходимостью нахождения среднего значения чисел. Это может быть полезно при расчетах статистики, определении средней оценки в классе или просто для интереса. Но как можно получить эту цифру без затруднений?
Существует несколько методов, позволяющих легко и точно определить среднее арифметическое числового ряда. Любой из них может быть использован в зависимости от конкретной ситуации и доступных данных. Важно помнить, что каждый метод обладает своими особенностями и применим только в определенных случаях.
Один из наиболее распространенных методов - это расчет среднего арифметического путем сложения всех чисел в ряду и деления полученной суммы на их количество. Этот подход прост и понятен даже для тех, кто не обладает большими знаниями в математике. Однако, в некоторых случаях, он может оказаться неточным и непоказательным.
Еще одним методом является использование формулы среднего арифметического для упорядоченного ряда чисел. Очень удобно применять этот способ, если вам уже предоставлены отсортированные данные. Формула заключается в нахождении суммы всех чисел с учетом их взвешивания по позиции в ряду.
Понятие арифметического среднего

Арифметическое среднее является результатом деления суммы всех чисел в наборе на их количество. Интуитивно можно представить среднее значение чисел как точку, которая находится где-то посередине между наибольшим и наименьшим числом. По сути, это число, которое наилучшим образом представляет общую характеристику всех чисел в наборе.
Для вычисления арифметического среднего набора чисел, нужно просуммировать все числа в наборе, затем поделить полученную сумму на количество чисел. Это простая операция, которая позволяет нам получить числовое значение, отображающее общую характеристику набора чисел. В следующих разделах мы рассмотрим более подробно, как можно вычислить среднее значение чисел и приведем примеры его использования в реальной жизни.
Нахождение среднего арифметического двух чисел

Если вам необходимо определить среднее значение двух чисел, то следующая инструкция поможет вам с легкостью достичь этой цели. Для начала, вам потребуется получить исходные числа, которые вы хотите усреднить.
Затем, для нахождения среднего значения, необходимо сложить эти два числа и разделить полученную сумму на 2. Это даст вам искомый результат.
| Шаг | Действие |
|---|---|
| 1 | Получите исходные числа, которые хотите усреднить. |
| 2 | Сложите эти два числа. |
| 3 | Разделите полученную сумму на 2. |
| 4 | Итоговое число является средним арифметическим исходных чисел. |
Следуя этим простым шагам, вы сможете легко найти среднее значение двух чисел без необходимости применения сложных математических формул.
Алгоритм для расчета среднего арифметического набора чисел
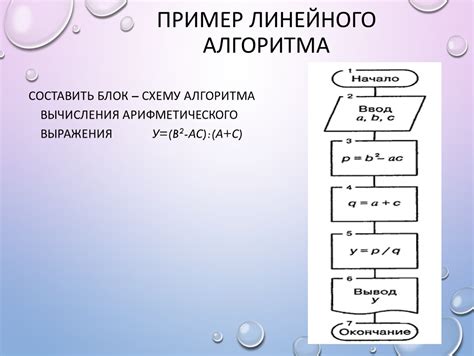
Прежде чем приступить к подсчету среднего значения чисел, необходимо иметь набор числовых данных. Этот набор может содержать произвольное количество чисел, больше одного. Идея заключается в том, что необходимо сложить все числа в наборе и разделить полученную сумму на количество чисел в наборе.
Для начала, создадим переменную для хранения суммы чисел в наборе, которую обозначим как "сумма". В данной переменной мы будем суммировать все числа из набора по мере их перебора. Затем, создадим еще одну переменную для хранения количества чисел в наборе, которую обозначим как "количество". В этой переменной мы будем подсчитывать количество чисел в наборе.
Далее, нам нужно перебрать каждое число из набора и добавить его к сумме, а также увеличить количество на единицу.
После того, как мы пройдем все числа в наборе и завершим перебор, мы можем рассчитать среднее значение. Для этого необходимо разделить сумму на количество и получить итоговое значение среднего.
Таким образом, алгоритм для подсчета среднего значения нескольких чисел заключается в следующих шагах:
- Создать переменную "сумма" и присвоить ей значение 0.
- Создать переменную "количество" и присвоить ей значение 0.
- Перебрать каждое число из набора, добавлять его к сумме и увеличивать количество на единицу.
- Рассчитать среднее значение, разделив сумму на количество.
Теперь, когда у вас есть алгоритм для подсчета среднего значения нескольких чисел, вы можете приступить к его реализации на практике.
Исключение некорректных значений при подсчете среднего

Определение корректности данных
Перед тем, как приступить к подсчету среднего значения, необходимо определить, что является некорректным значением. Некорректные значения могут включать различные ситуации, такие как отсутствие данных, ошибки в записи чисел, неподходящие значения, выбросы или выбивающиеся из общей тенденции числа, возникшие в результате ошибок ввода или других причин.
Обработка некорректных значений
При обнаружении некорректных значений, следует решить, каким образом их обрабатывать. Варианты включают исключение некорректных значений из расчетов, замену некорректных значений на среднее или другие корректные значения, или отбрасывание всей выборки, если она содержит существенное количество некорректных данных.
Значимость обработки некорректных значений
Успешная обработка некорректных значений играет важную роль в получении корректного результата при подсчете среднего. Некорректные данные могут быть результатом случайного или намеренного вмешательства, ошибок ввода или других факторов. Ответственность за обработку исключительных ситуаций и принятие решений, касающихся некорректных значений, лежит на исследователе или разработчике.
Исключение некорректных значений при подсчете среднего значения чисел является важным шагом для получения точного и надежного результата. Это требует определения корректности данных, выбора соответствующей стратегии обработки, и принятия ответственности за обработку исключительных ситуаций. Опытные исследователи и разработчики уделяют особое внимание обработке некорректных значений, чтобы повысить качество и достоверность своих результатов.
Применение среднего значения чисел в повседневной жизни

В реальной жизни среднее значение чисел играет важную роль, позволяя нам получить общую представление о данных, не зависимо от их масштаба. Мы используем среднее значение для оценки и сравнения результатов исследований, определения трендов и понимания статистической значимости различных феноменов.
В более практическом смысле среднее значение может быть полезно для принятия решений. Взятие среднего значения может помочь вам определить оптимальную цену для продукта или выявить наиболее эффективные стратегии маркетинга. Оно также может быть использовано для предсказания будущих трендов на основе исторических данных и помочь в принятии важных решений в бизнесе и экономике.
Кроме того, среднее значение может иметь практическое применение в области науки и техники. Например, в инженерии оно может помочь определить средний уровень шума в окружающей среде для разработки более эффективных систем шумоподавления. В медицине среднее значение может использоваться для определения нормальных показателей здоровья пациента или оценки эффективности нового лекарства на основе среднего результата в клинических исследованиях.
Примеры расчета среднего значения чисел

В этом разделе мы рассмотрим несколько примеров, которые помогут вам лучше понять процесс подсчета среднего значения чисел. Различные сценарии и задачи помогут вам применить эти знания на практике и лучше осознать принципы работы.
- Пример 1: Среднее значение списка оценок
- Пример 2: Среднее значение температур
- Пример 3: Среднее значение продаж
Допустим, у вас есть список оценок студентов по математике. Вам необходимо рассчитать среднюю оценку группы, чтобы понять, какой уровень успеваемости в ней преобладает. Мы покажем вам шаг за шагом, как подсчитать это среднее значение.
Давайте представим, что вы заинтересованы в изучении климата определенного района и собрали данные о ежедневных средних температурах за месяц. Используя эти данные, вы сможете рассчитать среднюю температуру за этот период и определить, какой климат преобладает в данном районе.
Вам необходимо оценить средние продажи за последние несколько месяцев, чтобы понять динамику продаж и проанализировать эффективность вашего бизнеса. Мы поможем вам вычислить среднее значение продаж и интерпретировать полученные данные.
Внимательное изучение этих примеров поможет вам научиться применять подсчет среднего значения чисел для решения различных задач. Успешное применение этих знаний в повседневной жизни и работе может существенно улучшить вашу аналитическую способность и помочь принимать более обоснованные решения.
Ошибки, которые нужно избегать при подсчете среднего арифметического

При расчете среднего арифметического чисел существуют определенные ошибки, которые следует избегать, чтобы получить корректный результат.
Во-первых, одной из распространенных ошибок является использование медианы или моды вместо среднего арифметического. Медиана представляет собой значение, которое находится в середине упорядоченного списка чисел, а мода - наиболее часто встречающееся значение. Использование этих показателей вместо среднего может привести к искажению результата и неправильной интерпретации данных.
Во-вторых, необходимо избегать игнорирования выбросов или аномальных значений при расчете среднего. Одно неправильное значение может значительно искажать результат. Если выбросы не являются ошибками в самих данных, то их необходимо учитывать при подсчете среднего значения.
В-третьих, некорректное округление или неправильное количество знаков после запятой может привести к неточному результату при расчете среднего. Необходимо учитывать, сколько знаков после запятой требуется в конкретной ситуации и округлять результат до нужного количества знаков.
В-четвертых, использование неправильного метода суммирования чисел может вызвать ошибку при расчете среднего арифметического. Необходимо использовать правильный метод суммирования, чтобы избежать неправильного результата.
В-пятыx, неправильное разделение и сбор данных во время расчета среднего также являются частыми ошибками. Все числа, которые требуется учесть при расчете среднего значения, должны быть правильно учтены и сложены, а затем разделены на правильное количество элементов.
И, наконец, неправильный выбор формулы для расчета среднего может также привести к ошибке. В зависимости от ситуации и типа данных следует выбрать подходящую формулу: среднее арифметическое арифметическое, взвешенное среднее, геометрическое среднее и т.д.
Как повысить точность вычисления среднего арифметического

Когда мы работаем с числами и нужно вычислить их среднее арифметическое, часто хотим получить наиболее точный результат. Повышение точности подсчета среднего значения может оказаться полезным во многих областях, включая статистику, финансы и научные исследования.
Существует несколько методов, которые помогут улучшить точность вычисления среднего значения чисел.
1. Исключение выбросов:
Выбросы - это значения, которые сильно отличаются от остальных чисел в наборе данных. Исключение выбросов перед вычислением среднего значения позволит получить более точный результат. Для идентификации выбросов можно использовать различные статистические методы, например, интерквартильный размах.
2. Учет весовых коэффициентов:
В некоторых случаях значения в наборе данных могут иметь различную важность или вес. Учет весовых коэффициентов при вычислении среднего значения позволяет учесть эту разницу и получить более точный результат. Коэффициенты веса можно задать вручную или использовать уже существующую информацию.
3. Использование взвешенного среднего:
В отличие от обычного среднего арифметического, взвешенное среднее учитывает не только количество значений, но и их вес. Этот метод особенно полезен, когда различные значения имеют разный вклад в итоговый результат и требуют учета их важности.
Применение указанных методов поможет повысить точность вычисления среднего значения чисел и получить более надежные результаты. Не забывайте применять и другие статистические методы для анализа данных и проверки корректности полученных результатов.
Вопрос-ответ

Каким образом можно вычислить среднее значение чисел?
Для вычисления среднего значения чисел следует суммировать все числа и разделить полученную сумму на их общее количество. Например, если имеется четыре числа: 5, 7, 10 и 3, можно найти среднее значение следующим образом: 5 + 7 + 10 + 3 = 25, а затем 25 / 4 = 6.25. Итак, среднее значение этих чисел равно 6.25.
Какие числа могут быть использованы для вычисления среднего значения?
Для вычисления среднего значения можно использовать любые числа - целые и дробные. Важно только учесть, что среднее значение будет иметь тот же тип чисел, которые используются для вычисления. Например, если все числа целые, то и среднее значение будет целым числом. Если среди чисел есть дробные, то и среднее значение будет дробным числом.
Можно ли вычислить среднее значение набора чисел без использования калькулятора или компьютера?
Да, можно вычислить среднее значение набора чисел без использования калькулятора или компьютера. Для этого необходимо просуммировать все числа вручную и затем разделить полученную сумму на их количество. Хотя это может быть трудоемким процессом, особенно при больших наборах чисел, но вполне возможным.
Как используется среднее значение в статистике?
Среднее значение, также известное как средняя арифметическая, является одним из основных показателей в статистике. Оно используется для описания центральной тенденции набора данных. Среднее значение позволяет узнать типичное значение в наборе чисел и сравнивать данные между собой. Например, при изучении доходов населения, среднее значение может показывать средний уровень дохода.



