Когда дело касается построения логических моделей или разработки сложных программных систем, неизбежно сталкиваешься с вопросом о нахождении оптимального решения. В эпоху насыщенной информацией и динамичных изменений, найти эффективные способы реализации становится критически важным. Именно здесь вступает на сцену ДНФ и СДНФ – мощные инструменты, которые способны оптимизировать и упростить процесс составления логических выражений.
Суть составления ДНФ и СДНФ заключается в выражении сложных логических операций через простые элементы. Как путь на витебскую землю, эти инструменты открывают нам дорогу к пониманию того, как составить логическую формулу наиболее эффективным образом. Они помогают нам разделить сложную задачу на более простые компоненты, исследовать каждую деталь и создать своего рода "карту маршрута" к решению.
Разумеется, эффективность и результативность составления ДНФ и СДНФ неотделимы от тщательного анализа и понимания работы логического выражения. Однако, вместе с тем, необходимо научиться преобразовывать условия задачи в формат, понятный компьютеру, чтобы получить оптимальное решение. В этом нам и помогают ДНФ и СДНФ: они позволяют нам избежать лишних операций и сосредоточиться на эффективном выполнении задачи.
Введение в тему: изучение базовых понятий теории ДНФ и СДНФ

На пути к пониманию и эффективной реализации методов составления Дизъюнктивной Нормальной Формы (ДНФ) и Совершенной Дизъюнктивной Нормальной Формы (СДНФ) важно разобраться в основных терминах и понятиях, которые лежат в их основе. Знание этих базовых концепций поможет нам более глубоко понять принципы и методы составления логических формул.
В этом разделе мы рассмотрим ключевые термины, которые используются в теории ДНФ и СДНФ. Например, мы исследуем понятие элементарного конъюнкта или слагаемого, которое играет важную роль в процессе составления ДНФ. Также мы изучим понятие элементарной дизъюнкции, которая является основным строительным блоком СДНФ.
Другим важным понятием, которое мы рассмотрим, будет литерал. Литерал представляет собой переменную или ее отрицание и играет ключевую роль в определении состояний или значений переменных в логических формулах.
| Термин | Описание |
|---|---|
| Элементарный конъюнкт | Логическое слагаемое, состоящее из переменных и их отрицаний, объединенных в логическую конъюнкцию |
| Элементарная дизъюнкция | Логическое слагаемое, состоящее из переменных и их отрицаний, объединенных в логическую дизъюнкцию |
| Литерал | Переменная или ее отрицание, используемые в логических формулах |
| Минтерм | Дизъюнкция всех литералов, соответствующих некоторой комбинации значений переменных |
| Макстерм | Конъюнкция всех литералов, соответствующих некоторой комбинации значений переменных |
Понимание данных понятий позволит нам продвинуться дальше и изучить методы составления ДНФ и СДНФ с помощью эффективных подходов и алгоритмов.
Различия между ДНФ и СДНФ

Во-первых, ДНФ - это логическая формула, которая представляет собой дизъюнкцию (логическое ИЛИ) наборов литералов, где каждый набор может быть либо положительным, либо отрицательным. При этом каждый набор литералов описывает определенное значение переменных. СДНФ, с другой стороны, является более компактной формой ДНФ, где каждый набор литералов представлен только один раз и содержит минимально возможное количество литералов.
Во-вторых, ДНФ часто используется для представления логической функции в аппаратуре и программной реализации. Ее применение облегчает анализ и вычисление значений функции. СДНФ, с другой стороны, является более предпочтительным в контексте алгоритмов оптимизации, так как позволяет уменьшить количество операций.
Таким образом, рассмотрение различий между ДНФ и СДНФ позволяет понять, как эти две концепции могут быть эффективно использованы в разных сферах, учитывая их преимущества и особенности структуры. Глубокое понимание этих различий помогает в оптимизации логических выражений и повышении эффективности их реализации.
Построение ДНФ: метод ковариаций
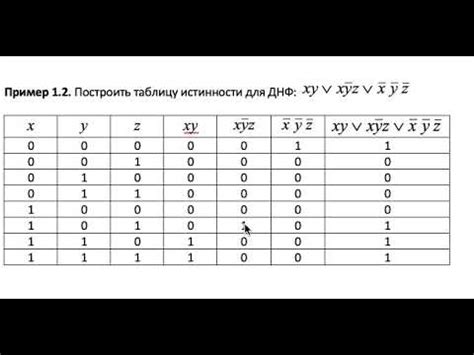
В данном разделе рассмотрим важный метод построения ДНФ (дизъюнктивной нормальной формы), основанный на анализе ковариаций между переменными. Этот метод позволяет эффективно определить логические связи между различными значениями переменных и создать компактное представление их комбинаций.
Метод ковариаций основан на понятии ковариационной матрицы, которая отражает степень зависимости между переменными во входных данных. Анализ ковариаций позволяет выявить наборы переменных, которые наиболее коррелируют между собой, и использовать эту информацию для построения ДНФ.
Как применять метод ковариаций при построении ДНФ? Сначала необходимо провести анализ входных данных и вычислить ковариационную матрицу. Затем можно выделить группы переменных, которые демонстрируют высокую степень корреляции, и объединить их в логические блоки в ДНФ. Это поможет сократить количество дизъюнкций и более компактно представить логическую функцию.
Преимущества метода ковариаций в построении ДНФ заключаются в его способности учитывать взаимосвязь между переменными и находить оптимальное представление функции. Это позволяет эффективно сократить размер ДНФ и упростить ее анализ и синтез.
Описание и пример применения метода ковариаций

Рассмотрение анализа зависимостей между случайными величинами позволяет использовать метод ковариаций для исследования и измерения силы связи между ними. Этот метод находит широкое применение в различных областях, таких как финансовая аналитика, статистика, экономические исследования и прогнозирование.
Метод ковариаций включает в себя определение и вычисление ковариации, которая даёт информацию о степени линейной зависимости между переменными. Чем ближе ковариация к нулю, тем слабее связь между величинами. Ковариация положительна, если величины изменяются вместе, и отрицательна, если они изменяются в противоположных направлениях. Применение метода ковариаций позволяет выявить как сильные, так и слабые зависимости между переменными и оценить их значимость.
Для наглядности, рассмотрим пример применения метода ковариаций в финансовой аналитике. Представим, что мы имеем две акции компаний A и B, и нам интересно установить, есть ли связь между их доходностями. С помощью метода ковариаций мы можем вычислить ковариацию доходности акций A и B за определенный период времени. Если ковариация положительна и значима, это может указывать на наличие положительной линейной зависимости между доходностями акций. Если ковариация отрицательна и значима, это может указывать на наличие отрицательной линейной зависимости между доходностями акций. Таким образом, метод ковариаций позволяет обнаружить тенденции и позволяет принимать взвешенные финансовые решения на основе анализа связей между переменными.
Построение ДНФ: метод карт Карно
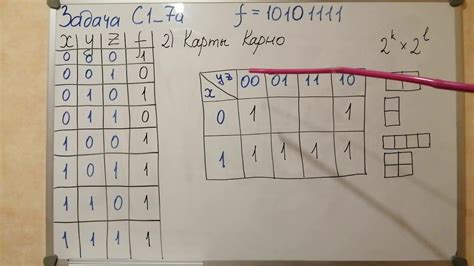
Карты Карно представляют собой таблицы, разделенные на ячейки, в которых размещаются булевы значения функции для соответствующих комбинаций входных переменных. Путем группировки и объединения соответствующих ячеек мы можем выделить схему ДНФ, которая будет полностью описывать функцию.
Для начала, необходимо построить таблицу и заполнить ее значениями булевой функции для всех возможных комбинаций переменных. Затем, используя карту Карно, мы можем сгруппировать соседние ячейки, содержащие единицы, в соответствии с логическими закономерностями функции. Группы формируют прямоугольники, которые будут использованы для определения значений переменных в ДНФ.
Ключевой преимущество метода карт Карно заключается в его простоте визуального представления и простоте анализа функции. Он позволяет наглядно увидеть взаимосвязь между входными переменными и значениями функции, что может помочь в определении наилучшей ДНФ.
Принципы работы и преимущества метода карт Карно
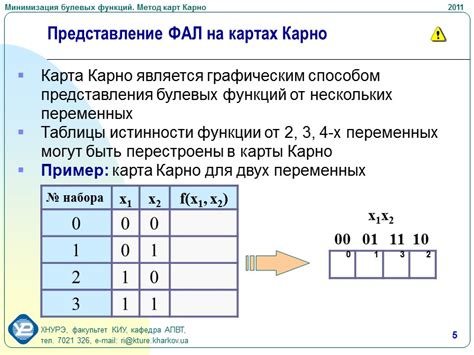
Принцип работы метода карт Карно заключается в разбиении исходной булевой функции на множество максимально простых импликант, которые собираются в группы. Для построения карты Карно используется пространство, в котором элементы функции располагаются с определенным порядком, что позволяет обнаружить закономерности и упростить выражение функции.
Основным преимуществом метода карт Карно является его наглядность и интуитивность. Графическое представление булевой функции в виде карта позволяет наглядно увидеть связь между ее элементами и выявить закономерности. Это значительно облегчает процесс минимизации функции и позволяет добиться более компактного выражения.
Кроме того, метод карт Карно обладает высокой эффективностью в сравнении с другими методами минимизации функций. Он позволяет находить оптимальное выражение функции без необходимости использования сложных математических выкладок или специальных алгоритмов. Это делает метод карт Карно доступным и простым для использования даже для неспециалистов в области логики и дискретной математики.
Приведение ДНФ к СДНФ

- Упрощение ДНФ: избавление от повторяющихся конъюнкций и минимизация числа логических операций.
- Получение минимальной ДНФ: использование методов, таких как метод Квайна или метод карт Карно, для нахождения минимального набора конъюнкций, представляющего данную функцию.
- Преобразование минимальной ДНФ в СДНФ: объединение конъюнкций с общими литералами и формирование выражения, в котором присутствуют все возможные комбинации литералов.
Эффективное приведение ДНФ к СДНФ позволяет существенно упростить вычисление логических функций и сократить объем памяти, необходимый для их хранения. Освоив такие методы, программисты смогут создавать более эффективные алгоритмы и оптимизировать работу своих программных решений.
Алгоритмы и примеры приведения ДНФ к СДНФ

Алгоритм 1: Использование законов алгебры логики
Существует несколько базовых законов алгебры логики, которые могут быть использованы для приведения ДНФ к СДНФ. Некоторые из них включают законы дистрибутивности, коммутативности и ассоциативности. Алгоритм 1 будет подробно рассматривать использование этих законов для приведения ДНФ к СДНФ. С помощью примеров будет показано, как применять каждый закон, и как они помогают преобразовывать ДНФ в СДНФ.
Алгоритм 2: Карта Карно и многообразие переменных
Карта Карно - это графическое представление логических функций с использованием квадратов и стрелок. Алгоритм 2 будет объяснять, как использовать карту Карно для приведения ДНФ к СДНФ. Примеры будут использованы для иллюстрации работы этого алгоритма.
Алгоритм 3: Методом основной дизъюнктивной нормальной формы
Основная дизъюнктивная нормальная форма (ОДНФ) - это популярный способ приведения ДНФ к СДНФ. Алгоритм 3 будет объяснять, как использовать данный метод для приведения ДНФ к СДНФ. С использованием примеров будет показано, как применять основную ДНФ для достижения желаемого результата.
Метод Квайна-МакКласки: оптимизация булевых функций

Метод Квайна-МакКласки основывается на представлении булевых функций в виде таблицы истинности и последующем разбиении множества строк этой таблицы на группы, содержащие строки с одинаковыми значениями функций. Далее происходит определение канонической ДНФ, которая представляет собой конъюнкцию минтермов, полученных из групп строк.
Применение метода Квайна-МакКласки позволяет уменьшить количество литералов и конъюнкций в выражении булевой функции, что в свою очередь повышает ее эффективность и упрощает процесс анализа и проектирования логических схем.
Идея и примеры применения метода Квайна-МакКласки
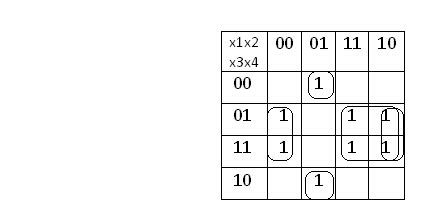
Главная идея метода Квайна-МакКласки заключается в разделении исходного булевого выражения на максимально возможное количество простых импликант, которые затем комбинируются для получения минимальной ДНФ. Для этого используется таблица Квайна, где каждый столбец соответствует всевозможным простым импликантам, а каждая строка - наборам, на которых импликанты равны единице.
| Наборы | Простые импликанты | ||
| А | В | C | |
| Набор 1 | 1 | 0 | 1 |
| Набор 2 | 1 | 1 | 0 |
| Набор 3 | 0 | 1 | 1 |
Применяя метод Квайна-МакКласки, мы можем упростить булево выражение до минимального количества импликант и получить его ДНФ. Такой подход не только позволяет сократить количество логических операций в выражении, но и сделать его более читаемым и понятным для дальнейшего анализа и оптимизации.
Пример применения метода Квайна-МакКласки:
Дано булево выражение: (A ∧ B) ∨ (¬A ∧ C)
Составляем таблицу Квайна:
| Наборы | Простые импликанты | ||
| A | B | C | |
| Набор 1 | 0 | 0 | 1 |
| Набор 2 | 0 | 1 | 1 |
| Набор 3 | 1 | 0 | 1 |
| Набор 4 | 1 | 1 | 0 |
Из таблицы Квайна видно, что простыми импликантами являются следующие выражения:
А ∨ ¬В ∨ С
¬А ∨ B ∨ С
Объединяя эти простые импликанты, получаем минимальную ДНФ для исходного булевого выражения.
Вопрос-ответ

Какие основные принципы составления ДНФ?
Основные принципы составления ДНФ включают в себя выделение всех импликант, которые равны 1, исключение из импликант всех ячеек значений, равных 0, и объединение оставшихся импликант в ДНФ.
Какие есть эффективные способы реализации ДНФ?
Существует несколько эффективных способов реализации ДНФ, включая использование таблиц истинности, метода Квайна, алгоритма Квайна-МакКласки и метода Петрик-Голдберга. Каждый из этих методов имеет свои особенности и может быть применен в зависимости от размера и сложности функции.
Какова роль СДНФ в составлении логических функций?
СДНФ (сокращенная дизъюнктивная нормальная форма) играет важную роль в составлении логических функций, так как она представляет функцию в виде логического выражения, включающего только те переменные, которые принимают значение 1 при функции. СДНФ позволяет более компактно и эффективно представить логическую функцию, что упрощает ее анализ и реализацию.



