Мир полон движений: вращающихся колес, крутящихся механизмов, взлетающих птиц. В основе этих процессов лежит одно неотъемлемое понятие – угловая динамика. С помощью нее мы можем понять, как объекты изменяют свою ориентацию в пространстве и какова скорость их вращения.
Представьте себе на мгновение, что вы наблюдаете за вертящейся звездой на небосводе. На первый взгляд показательно и красиво, но эта огромная звезда хранит в себе тайну – угловую скорость. Она является одним из ключевых показателей, определяющих траекторию вращения звезды вокруг своей оси.
Угловая скорость играет важную роль в механике и физике. Она описывает, насколько быстро тело вращается вокруг своей оси и может быть как постоянной, так и изменяющейся величиной. Но как найти эту скорость через угловое ускорение, которое связано с изменением угловой скорости? В этой статье мы разберемся в основных принципах и формулах, позволяющих определить угловую скорость исходя из углового ускорения.
Основные понятия: связь между угловой скоростью и угловым ускорением
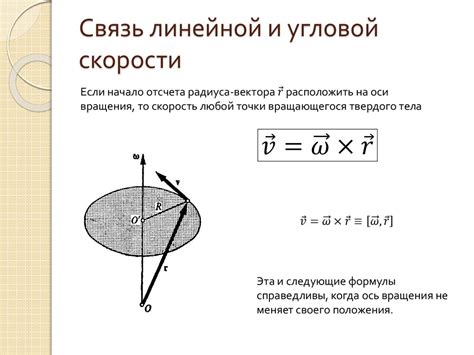
Угловая скорость выражает скорость изменения угла поворота тела в единицу времени. Она может быть положительной или отрицательной в зависимости от направления вращения: против часовой стрелки или по часовой стрелке, соответственно. Угловая скорость измеряется в радианах в секунду (рад/с) или в градусах в секунду (град/с).
Угловое ускорение, в свою очередь, определяет скорость изменения угловой скорости. Иными словами, оно показывает, насколько быстро угловая скорость меняется с течением времени. Угловое ускорение также может быть положительным или отрицательным, указывая на увеличение или уменьшение угловой скорости. Единицы измерения углового ускорения аналогичны угловой скорости: радианы в секунду в квадрате (рад/с²) или градусы в секунду в квадрате (град/с²).
Связь между угловой скоростью и угловым ускорением представляет собой фундаментальный аспект изучения вращательного движения. Понимание этих понятий позволяет описывать и анализировать поведение вращающихся объектов как в естественных, так и в технических системах, а также решать различные задачи, связанные с кинематикой и динамикой вращения.
Таким образом, угловая скорость и угловое ускорение являются важными концепциями, которые помогают понять и визуализировать движение вращающихся объектов, а также описывать его изменения во времени. Их изучение позволяет расширить наши знания о физическом мире и применить их на практике для решения различных задач и создания новых технологий.
Формула вычисления скорости при изменении объемлемого угла движения

Для вычисления угловой скорости используется формула, включающая угловое ускорение, которое можно рассматривать как меру изменения угловой скорости в единицу времени. Разница между мгновенными значениями угловой скорости и ускорения заключается в том, что скорость выражает отношение перемещения к затраченному времени, в то время как угловая скорость оценивает соответствующие изменения в угловом перемещении объекта.
Формула для определения угловой скорости через угловое ускорение выглядит следующим образом: угловая скорость = угловое ускорение × время. Зная значение углового ускорения и время, мы можем вычислить угловую скорость, что поможет нам лучше понять и описать движение вращающегося объекта.
Важно отметить, что угловая скорость обычно измеряется в радианах в секунду (рад/с), а угловое ускорение - в радианах в секунду в квадрате (рад/с²). Формула позволяет связать данные две величины и получить информацию о скорости соответствующего вращения.
Связь между скоростью вращения и ускорением вращения

В этом разделе будет рассмотрена общая формула, которая связывает угловую скорость и угловое ускорение в системе вращающегося тела.
| Символ | Обозначение |
| ω | Угловая скорость |
| α | Угловое ускорение |
| r | Расстояние от оси вращения до точки с интересующей нас скоростью |
Для объяснения связи между скоростью вращения и ускорением вращения необходимо понять, что угловая скорость представляет собой меру изменения угла поворота вращающегося тела относительно времени. Угловое ускорение, в свою очередь, указывает на изменение угловой скорости в единицу времени.
Формула, которая выражает связь между угловой скоростью и угловым ускорением, представляет собой уравнение:
ω = α * r
где ω - угловая скорость, α - угловое ускорение, r - расстояние от оси вращения до точки, скорость которой интересует.
Таким образом, эта формула позволяет определить угловую скорость вращающегося тела, зная его угловое ускорение и расстояние от оси вращения до интересующей точки.
Применение формул к задачам на определение скорости вращения при заданном ускорении
Представим себе ситуацию, когда катер стартовал с места и ускоряется с постоянным угловым ускорением вокруг вертикальной оси. Нам известно значение углового ускорения и мы хотим определить угловую скорость катера в данный момент времени. Для этого воспользуемся формулой связи угловой скорости с угловым ускорением:
Угловая скорость (ω) = Угловое ускорение (α) × Время (t)
Теперь рассмотрим конкретные задачи, чтобы проиллюстрировать применение данной формулы. Например, при известном угловом ускорении, можно определить угловую скорость вращения планеты вокруг своей оси за определенное время. Также, данная формула может быть использована для определения угловой скорости вращения маятника, зная его ускорение и время.
Важно понимать, что эти примеры лишь небольшая часть возможных задач, в которых требуется определить угловую скорость через угловое ускорение. Подходящая формула зависит от контекста задачи и основных известных величин. Следует всегда быть внимательными при анализе конкретной ситуации и выбирать соответствующую формулу для решения.
Пример 1: твердое тело с равномерно увеличивающимся угловым ускорением

В этом примере рассмотрим движение твердого тела, которое совершает вращение вокруг некоторой оси. Угловое ускорение, также известное как ускорение вращения, представляет собой меру изменения скорости вращения тела. В данном случае, угловое ускорение остается постоянным со временем.
Представьте себе, что вы наблюдаете качание маятника, который состоит из твердого стержня и точки подвеса. Этот маятник начинает движение из начального положения и ускоряется вращательным образом. Как определить его угловую скорость в любой момент времени?
Для решения этой задачи мы можем использовать уравнения кинематики движения твердого тела. В данном примере, мы будем рассматривать только простую ситуацию, когда угловое ускорение остается постоянным со временем.
Мы можем воспользоваться формулой, связывающей угловое ускорение и угловую скорость с временем. Данная формула позволяет нам вычислить угловую скорость, зная угловое ускорение и время, прошедшее с начала движения:
Угловая скорость = Начальная угловая скорость + Угловое ускорение * Время
Таким образом, если у нас есть начальная угловая скорость и угловое ускорение, мы можем определить угловую скорость твердого тела в любой момент времени, используя данную формулу.
Пример 2: движение тела с изменчивым угловым ускорением

В предыдущем разделе мы рассмотрели случай движения тела с постоянным угловым ускорением, однако в реальных ситуациях угловое ускорение может быть переменным. В этом примере мы рассмотрим такой случай и изучим, как это влияет на угловую скорость тела.
Для лучшего понимания понятий переменного углового ускорения и его влияния на движение тела, представим, что у нас есть тело, которое движется по окружности. В начале его движения угловое ускорение имеет одно значение, затем оно постепенно изменяется по ходу времени.
Изменение углового ускорения влечет за собой изменение угловой скорости тела. При постоянном ускорении угловая скорость тела растет равномерно, а в случае переменного углового ускорения ее изменение не будет таким линейным. Здесь важно учитывать не только само значение угловой скорости, но и ее направление.
Для определения угловой скорости в случае переменного углового ускорения необходимо использовать уравнение, которое учитывает как значение углового ускорения, так и угол поворота со временем. Это позволяет учесть все изменения, происходящие в движении тела, и получить более точные результаты.
- Исходя из уравнения движения с переменным угловым ускорением, можно определить угловую скорость тела в любой момент времени.
- Важно учитывать, что при переменном угловом ускорении угловая скорость тела может меняться не только по величине, но и по направлению.
- Изменение угловой скорости может быть как положительным, так и отрицательным в зависимости от значений углового ускорения и времени.
Пример движения тела с переменным угловым ускорением демонстрирует, что значения угловой скорости и углового ускорения тесно связаны, и для полного понимания движения тела необходимо учитывать все эти факторы вместе.
Применение полученных результатов в реальной жизни

Разобравшись в процессе определения угловой скорости через угловое ускорение, мы можем применить эти знания в различных аспектах реальной жизни. От управления машиностроительными системами до спортивных достижений, понимание угловой скорости и углового ускорения имеет широкий диапазон применения.
В машиностроении и автоматизации, знание угловой скорости и углового ускорения позволяет оптимизировать работу робототехнических систем, улучшить точность и эффективность их движения. Это особенно важно при создании роботов, которые должны выполнять сложные задачи с высокой точностью, например, в производстве или медицинской индустрии.
В спорте угловая скорость и угловое ускорение широко используются для анализа и развития техники в различных видов спорта. Например, в гимнастике или фигурном катании, понимание угловой скорости и углового ускорения позволяет атлетам совершенствовать свои трюки и элементы, контролировать свое положение в воздухе и достигать лучших результатов. Точный расчет угловой скорости и углового ускорения также помогает тренерам разрабатывать более эффективные тренировочные программы и прогнозировать потенциал атлетов.
Исследования в астрономии также полагаются на понимание угловой скорости и углового ускорения. Они позволяют ученым изучать движение планет, звезд и галактик, анализировать их эволюцию и искать закономерности в космическом пространстве.
Таким образом, знание и применение угловой скорости и углового ускорения имеют широкий спектр применения в различных сферах, от машиностроения и спорта до астрономии и других научных областей. Понимание этих концепций позволяет совершенствовать технику и улучшать результаты, а также помогает в разработке новых технологий и научных исследований.
Примеры применения угловой скорости и углового ускорения в различных областях

В мире существует множество областей, где угловая скорость и угловое ускорение играют важную роль. Они находят свое применение в различных сферах науки, техники, спорта и даже в повседневной жизни. Угловая скорость и угловое ускорение представляют собой показатели, которые описывают вращательное движение и помогают в изучении его характеристик.
| Область применения | Примеры |
|---|---|
| Физика | Рассмотрение движения планет вокруг своих осей, моделирование работы ветряных мельниц, анализ вращения колеса автомобиля. |
| Механика | Исследование работы гирь и маятников, разработка механизмов с вращательным движением, проектирование приводных систем. |
| Астрономия | Анализ вращения звезд и галактик, изучение движения планет и спутников, определение их ориентации в пространстве. |
| Спорт | Оценка быстроты вращения велосипедных колес, изучение техники прыжков в фигурном катании, разработка тренировочных упражнений для спортсменов. |
| Технологии | Проектирование роботов с вращательными механизмами, разработка систем стабилизации и ориентирования космических аппаратов, создание прецизионных приборов. |
Каждая из этих областей использует угловую скорость и угловое ускорение для анализа, оптимизации и контроля вращательных движений. Знание этих понятий позволяет ученым, инженерам и специалистам прогнозировать поведение объектов, создавать эффективные механизмы, а также разрабатывать новые технические и научные решения.
Вопрос-ответ

Как найти угловую скорость через угловое ускорение?
Для того чтобы найти угловую скорость через угловое ускорение, необходимо знать значение углового ускорения и радиус вращающегося объекта. Угловая скорость вычисляется по формуле: угловая скорость = угловое ускорение * радиус.
Как определить угловую скорость, если известно только угловое ускорение?
Если известно только значение углового ускорения, то для определения угловой скорости необходимо также знать радиус вращающегося объекта. После этого угловую скорость можно вычислить по формуле: угловая скорость = угловое ускорение * радиус.
Можно ли найти угловую скорость через угловое ускорение, если неизвестен радиус вращающегося объекта?
Нет, нельзя найти угловую скорость через угловое ускорение без знания радиуса вращающегося объекта. Радиус является необходимым параметром для расчета угловой скорости по формуле: угловая скорость = угловое ускорение * радиус.
Каким образом можно определить угловое ускорение?
Угловое ускорение можно определить, зная угловую скорость и время, за которое она меняется. Угловое ускорение вычисляется по формуле: угловое ускорение = (изменение угловой скорости) / (изменение времени).
Почему в формуле для расчета угловой скорости используется радиус?
Радиус входит в формулу для расчета угловой скорости, так как он определяет расстояние от оси вращения до точки на объекте. Изменение радиуса приводит к изменению длины пути, пройденного точкой на объекте за определенный промежуток времени, что влияет на ее скорость вращения.
Как найти угловую скорость через угловое ускорение?
Угловая скорость может быть найдена через угловое ускорение при помощи формулы: угловая скорость = угловое ускорение * время. Для этого необходимо знать значение углового ускорения и время, в течение которого оно действует.



