Определяя скорость вращения: разгадываем тайны частоты
В мире, где движение всегда сопровождает нас, понимание его основных параметров становится ключом к познанию окружающей нас реальности. Один из таких параметров - частота вращения. Это своеобразный язык, на котором загадываются все преобразования движения, от пульсирующей звезды до пикселя на экране.
В рамках этой статьи мы хотим рассмотреть довольно замысловатую задачу - определение угловой скорости именно через частоту вращения. Угловая скорость - это наглядная мера того, насколько быстро происходит вращение объекта вокруг своей оси. Этот параметр обладает особой важностью в технических и физических процессах, поэтому его определение - задача не из простых.
Основные понятия и определения угловой скорости

Величина угловой скорости может быть измерена в радианах в секунду (рад/с), градусах в секунду (°/с) или оборотах в минуту (об/мин). Она позволяет определить, с какой интенсивностью объект вращается вокруг своей оси. При этом, частота вращения – другая важная характеристика – определяет количество полных оборотов, совершаемых объектом за определенный промежуток времени. Частоту вращения можно выразить в герцах (Гц) или оборотах в минуту (об/мин).
Понимание и определение угловой скорости важно для различных областей, включая механику твердого тела, аэродинамику, робототехнику, астрономию и многое другое. Угловая скорость позволяет описывать и предсказывать движение вращающихся объектов, а также является базовым понятием для понимания кинематики и динамики поворотных систем.
Основы угловой скорости

Чтобы понять суть угловой скорости, необходимо вспомнить базовые понятия физики. Вращение - это движение, при котором тело поворачивается вокруг оси. Угол поворота, который происходит за определенный промежуток времени, определяет угловую скорость. Это позволяет нам измерять скорость изменения угла и оценивать, насколько быстро тело вращается.
Существует несколько способов измерения угловой скорости. Один из них - измерение количества оборотов (или полных витков) тела в минуту. Эта величина называется частотой вращения и измеряется в оборотах в минуту. При необходимости можно перевести частоту вращения в радианы в секунду, умножив ее на коэффициент 2π/60. Именно это исчисление и позволяет нам определить угловую скорость.
Итак, угловая скорость - это величина, которая описывает изменение угла поворота тела вращения за определенное время. Она измеряется в радианах в секунду и может быть определена путем измерения частоты вращения тела и преобразования ее в радианы в секунду.
| Примеры частоты вращения и соответствующей угловой скорости | |
|---|---|
| Частота вращения равна 100 об/мин | Угловая скорость равна π/3 рад/с |
| Частота вращения равна 50 об/мин | Угловая скорость равна π/6 рад/с |
| Частота вращения равна 200 об/мин | Угловая скорость равна 2π/3 рад/с |
Влияние скорости оборотов на вычисление угла поворота
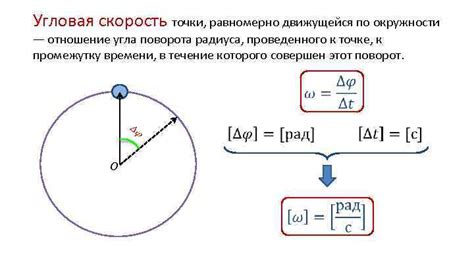
Частота вращения представляет собой количество оборотов объекта за единицу времени. В зависимости от скорости вращения, определение угловой скорости может обладать различной точностью. Для низких частот вращения, когда объект совершает медленные повороты, определение угловой скорости проще и точнее.
Однако при высоких частотах вращения возникают определенные сложности. Быстрое изменение положения объекта в пространстве требует более точных и чувствительных методов измерения, так как даже незначительная погрешность может привести к неточному определению угловой скорости.
Для успешного определения угловой скорости при высоких частотах вращения необходимы специализированные инструменты и методы измерения. Это могут быть, например, гироскопы или акселерометры, которые способны обрабатывать большой объем данных и выдавать точные результаты. Также важно обеспечить стабильность измеряемого объекта, чтобы исключить внешние воздействия и уменьшить возможные погрешности.
В целом, частота вращения оказывает влияние на определение угловой скорости, и ее учет при выборе метода измерения является важным фактором. При работе с объектами, вращающимися с высокой скоростью, следует учитывать особенности определения угловой скорости и использовать соответствующие средства измерения для достижения наибольшей точности и надежности результатов.
Определение угловой скорости с использованием периода вращения

Один из способов определения угловой скорости с использованием периода вращения заключается в применении следующей формулы:
- Угловая скорость = 2π / Период вращения
В этой формуле переменные "Угловая скорость" и "Период вращения" выражены в соответствующих единицах измерения. Угловая скорость измеряется в радианах в секунду, а период вращения - в секундах.
Для более точных вычислений угловой скорости можно использовать дополнительные измерительные устройства, такие как гироскопы или энкодеры. Гироскопы представляют собой устройства, способные измерять угловую скорость вращения объекта, а энкодеры - датчики, фиксирующие изменение угла поворота. Эти данные могут быть использованы для расчета угловой скорости с высокой точностью и надежностью.
Таким образом, определение угловой скорости с использованием периода вращения представляет собой важный и доступный метод измерения, который может быть применен в различных областях, таких как физика, механика, робототехника и другие.
Расчет угловой скорости при заданной частоте вращения и радиусе
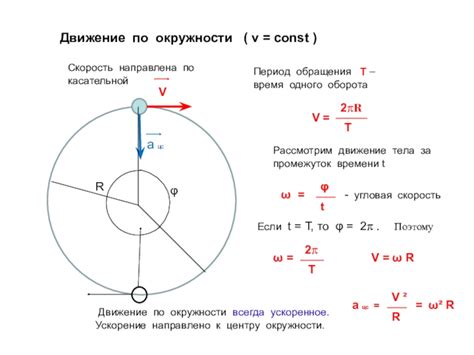
В данном разделе рассмотрим способы определения угловой скорости, основываясь на известной частоте вращения и радиусе объекта. Угловая скорость представляет собой величину, характеризующую скорость вращения объекта вокруг своей оси. Расчет данной величины может быть полезен в различных областях, таких как физика, механика или технические науки.
Для начала, необходимо определиться с понятиями. Частота вращения является числовым значением, которое описывает количество полных оборотов объекта в единицу времени. Радиус, в свою очередь, представляет собой расстояние от оси вращения до точки на объекте. Эти две величины являются ключевыми для определения угловой скорости.
- Один из способов расчета угловой скорости состоит в использовании формулы: угловая скорость (ω) равна произведению частоты вращения (f) на 2π (два пи) - основной математической константу. Таким образом, можно получить выражение ω = 2πf.
- Другой метод основывается на радиусе объекта. Угловая скорость (ω) прямо пропорциональна частоте вращения (f) и обратно пропорциональна радиусу (r). Можно использовать формулу: ω = 2πf / r, где 2πf - линейная скорость объекта при данной частоте вращения.
- Также, при известных значениях линейной скорости (v) и радиуса (r), можно расчитать угловую скорость (ω) по формуле: ω = v / r. Для этого необходимо знать как линейную скорость, так и радиус, либо иметь возможность их измерить.
Расчет угловой скорости при известной частоте вращения и радиусе является важной задачей, позволяющей определить скорость вращения объекта и его движение в пространстве. Используя соответствующие формулы, можно получить числовые значения угловой скорости, которые могут быть применены в различных научных и технических расчетах.
Вопрос-ответ

Каким способом можно определить угловую скорость по частоте вращения?
Для определения угловой скорости по частоте вращения необходимо знать соотношение между частотой и угловой скоростью. Для этого можно использовать соотношение w = 2пf, где w - угловая скорость, f - частота вращения. Если известна частота вращения, умножив ее на 2п, можно получить угловую скорость.
Можно ли определить угловую скорость по частоте вращения без знания радианной меры?
Да, можно. Для этого нужно знать количество оборотов в секунду и использовать следующую формулу: w = 2пf. Если у вас есть информация о количестве оборотов в секунду, умножив его на 2п, вы сможете определить угловую скорость без необходимости знания радианной меры.



