Ежедневная жизнь часто накладывает на нас разнообразные математические задачи, требующие поиска нестандартных решений. Одной из таких задач является определение площади квадрата по его диагонали. Вместо использования запутанных формул и сложных алгоритмов, сегодня мы рассмотрим простой и доступный способ нахождения этого значения без лишних усилий и достаточно захватывающего заинтересованность методом.
В основе данного метода лежит мысль о том, что каждый квадрат можно разделить на два равнобедренных прямоугольных треугольника. Это открытие дает нам возможность использовать уже хорошо известную формулу для нахождения площади прямоугольного треугольника. Вы, конечно же, уже догадались, что нам понадобятся значения длины катетов, а учитывая, что данная задача предполагает нахождение площади квадрата, в ней нам почти всегда будет известна диагональ.
Итак, продолжаем наше размышление. Если мы знакомы с теоремой Пифагора, то знаем, что квадрат гипотенузы равен сумме квадратов катетов. В случае квадрата, гипотенузу можно представить в виде двух диагоналей, а значит, по теореме Пифагора, каждая диагональ будет являться гипотенузой своего треугольника. Теперь мы уже имеем два прямоугольных треугольника, каждый из которых имеет равную длину диагонали и катеты, равные сторонам квадрата, то есть, диагонали разделена пополам.
Эффективный и простой алгоритм вычисления площади квадрата без использования формул

В данном разделе мы представим эффективный и простой способ рассчитать площадь квадрата, не прибегая к использованию сложных математических формул или измерению диагонали. Этот алгоритм позволит вам быстро и точно найти площадь квадрата, используя лишь имеющуюся информацию о его стороне.
Шаг 1: Определите длину стороны квадрата. Для этого можно воспользоваться линейкой или другим измерительным инструментом.
Шаг 2: Возведите полученное значение в квадрат, умножив его само на себя. Например, если длина стороны равна 5 см, то вычисление будет выглядеть следующим образом: 5 x 5 = 25.
Шаг 3: Полученное число является площадью квадрата. Например, для квадрата со стороной 5 см, его площадь равна 25 квадратных сантиметров.
Таким образом, использование данного простого алгоритма позволяет быстро и легко определить площадь квадрата, обходя сложные формулы и измерение диагонали.
Геометрическое решение: определяем сторону квадрата по диагонали
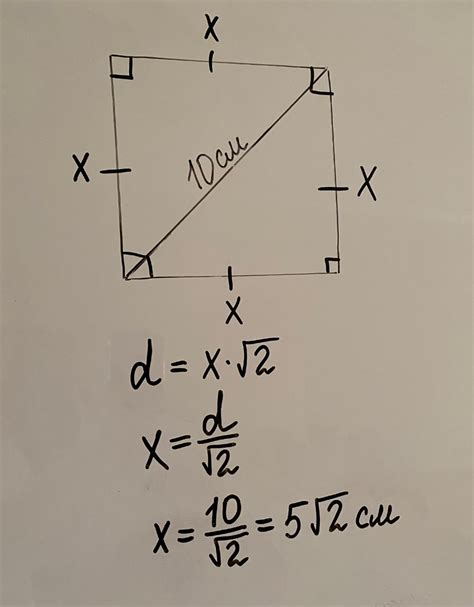
В данном разделе рассмотрим интересный подход для определения стороны квадрата на основе известной диагонали. Вместо применения сложных формул и алгоритмов, мы воспользуемся простой геометрической идеей.
Практическое применение: использование физических объектов для вычисления площади квадрата
Вместо того, чтобы полагаться на математические вычисления, мы можем использовать физические объекты, такие как линейка или шагометр, для измерения стороны квадрата. Используя эти измерения, мы можем затем создать копию квадрата с помощью бумаги или другого материала и собрать его, используя ленту или клей.
После этого, мы можем взять нашу копию квадрата и разрезать его по диагонали, получив два равнобедренных треугольника. Затем, мы можем положить эти треугольники рядом, чтобы они образовали прямоугольник, и затем измерить длину и ширину прямоугольника с помощью тех же физических объектов, какими мы измеряли сторону квадрата ранее.
После того, как мы измерили длину и ширину прямоугольника, нам просто нужно умножить эти два числа вместе, чтобы получить его площадь. Эта площадь будет эквивалентна площади нашего исходного квадрата.
- Использование физических объектов и реальных предметов для вычисления площади квадрата позволяет нам обратиться к конкретным и знакомым материалам и методам.
- Этот метод интуитивен и понятен даже для тех, кто не имеет математического образования, и может быть использован в повседневной жизни.
- Практическое применение физических объектов в геометрии позволяет ученикам лучше визуализировать и понять концепцию площади квадрата.
Альтернативный подход: вычисление площади квадрата с использованием тригонометрических соотношений

В этом разделе мы рассмотрим альтернативный подход к вычислению площади квадрата. Вместо использования обычных формул и определений, мы будем пользоваться тригонометрическими соотношениями для нахождения этого параметра без применения сложных математических операций. Такой подход позволяет упростить вычисления и получить результат без необходимости запоминать формулы или применять сложные шаги.
В начале нашего исследования мы подробно рассмотрим тригонометрические соотношения, связанные с углами и сторонами квадрата. Затем мы покажем, как эти соотношения можно использовать для вычисления площади квадрата. Мы представим примеры и детально объясним каждый шаг, чтобы у вас не возникало затруднений при применении этого подхода в практических задачах.
- Рассмотрим основные тригонометрические функции, такие как синус, косинус и тангенс, и их связь с углами квадрата.
- Обсудим, как определить значения этих функций для заданного угла, используя соответствующие таблицы или калькулятор.
- Разберемся, как применять эти соотношения для нахождения длины стороны квадрата, используя заданную диагональ.
- Затем мы узнаем, как вычислить площадь квадрата, зная только значения тригонометрических функций и длину диагонали.
В результате вы сможете применить альтернативный подход к вычислению площади квадрата, использовав тригонометрические соотношения, которые сделают эту задачу более интуитивной и понятной. Этот метод может быть полезен в различных ситуациях, где необходимо быстро определить площадь квадрата при наличии только диагонали и знаний о тригонометрии.
Вопрос-ответ

Как получить площадь квадрата по его диагонали без использования формулы?
Чтобы найти площадь квадрата по его диагонали без формулы, можно использовать простой способ. Для этого нужно возвести длину диагонали в квадрат и поделить полученное значение на два.
Можно ли найти площадь квадрата, если известна только его диагональ?
Да, это возможно. Если известна длина диагонали квадрата, то можно найти его площадь с помощью простого способа. Для этого нужно возвести длину диагонали в квадрат и поделить полученное значение на два.
Каким образом можно получить площадь квадрата, если известна только его диагональ?
Если вам известна длина диагонали квадрата и вы хотите найти его площадь без использования формулы, вы можете возвести длину диагонали в квадрат и поделить полученное значение на два. Это позволит вам получить площадь квадрата.
Как найти площадь квадрата, если известна его диагональ?
Если вам известна длина диагонали квадрата, вы можете найти его площадь без использования формулы. Просто возьмите длину диагонали, возвести ее в квадрат и поделите полученное значение на два. Это даст вам площадь квадрата.
Каким образом можно вычислить площадь квадрата, зная только длину его диагонали?
Если вам известна длина диагонали квадрата, вы можете без формулы найти его площадь. Просто возведите длину диагонали в квадрат и поделите полученное значение на два. Таким образом, вы получите площадь желаемого квадрата.



