В геометрии есть задачи, с которыми мы сталкиваемся в повседневной жизни. Одна из таких задач – определение гипотенузы прямоугольного треугольника. Для того чтобы решить эту задачу без особых трудностей, существует простой приём расчёта, который позволяет получить точный результат.
Каким образом можно найти гипотенузу? Для начала необходимо определить длины катетов и угол, образованный ими. Используя элементарные геометрические преобразования, можно получить значение гипотенузы с уверенностью в его точности.
В процессе расчёта рекомендуется использовать следующий приём: пользуясь теоремой Пифагора, можно найти длину гипотенузы с помощью косинуса угла между катетами. Такой способ значительно упрощает процесс расчёта и позволяет получить достоверный результат.
Описание роли гипотенузы в прямоугольном треугольнике
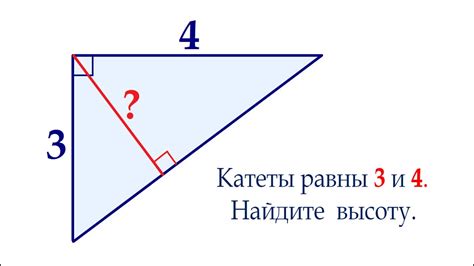
Функции гипотенузы:
- Обеспечивает стабильность треугольника;
- Определяет главное направление в треугольнике;
- Является основной измеряемой величиной в задачах связанных с прямоугольными треугольниками;
- Сочетает в себе синусы и косинусы углов треугольника, что позволяет определить их величину.
Измерение и использование гипотенузы имеет большое значение в научных, технических и строительных областях, а также в практических задачах, связанных с прямоугольными треугольниками. Независимо от цели изучения, гипотенуза является неотъемлемой частью этого треугольника и определяет его основные свойства и особенности.
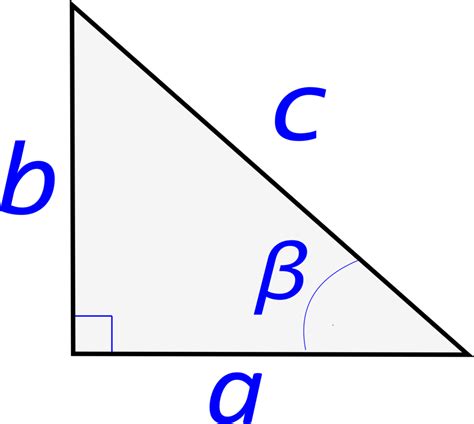
Обозначение сторон треугольника и между ними угла
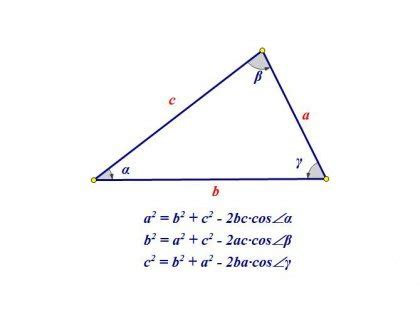
Когда мы говорим о треугольнике, существуют специальные обозначения для его сторон, которые называются катетами, а также для угла между этими сторонами. Эти обозначения позволяют нам легко идентифицировать и работать с разными элементами треугольника.
Первый катет обычно обозначается буквой "а" или "b", второй катет - буквой "с". Угол, образованный между этими катетами, часто обозначается греческой буквой "θ" (тета) или другой подходящей нотацией.
- Катет "а"
- Катет "b"
- Катет "с"
Обозначение катетов и угла между ними является важным аспектом решения задач по нахождению гипотенузы. Используя эти обозначения, можно легко проводить вычисления и анализировать свойства треугольника с точки зрения его геометрических характеристик.
Знание и понимание обозначения катетов и угла между ними поможет вам эффективно применять простой способ расчета гипотенузы и решать различные задачи, связанные с треугольниками.
Теорема Пифагора и ее применение в расчетах
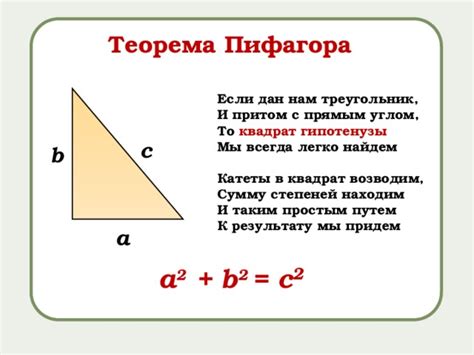
В математике существует одна фундаментальная теорема, которая нашла широкое применение во многих областях: это теорема Пифагора. В основе этой теоремы лежит взаимосвязь между длинами сторон прямоугольного треугольника и его гипотенузой. Благодаря этой теореме, мы можем вычислить длину гипотенузы, зная длины катетов и угол, образованный ими.
Применение теоремы Пифагора может быть полезно при решении различных задач, связанных с прямоугольными треугольниками. Например, если нам известны длины двух катетов и угол между ними, мы можем легко вычислить длину гипотенузы. Для этого используется простая формула, которая базируется на теореме Пифагора.
- Найдем синус угла между катетами, используя соотношение между противолежащей стороной и гипотенузой в прямоугольном треугольнике.
- Зная синус угла и длины одного из катетов, можно вычислить длину противолежащей стороны.
- С помощью теоремы Пифагора найдем длину гипотенузы как квадратный корень из суммы квадратов длин двух катетов.
Такой подход позволяет нам легко решать задачи, где требуется найти гипотенузу по длинам катетов и углу, образованному ими. Будь то задачи из геометрии или физики, теорема Пифагора с ее применением в расчетах становится незаменимым инструментом для упрощения и точности получаемых результатов.
Примеры применения теоремы Пифагора

| Пример 1: Вычисление длины троса |
|---|
| Рассмотрим ситуацию, когда необходимо вычислить длину троса, который нужно закрепить между двумя стойками, расположенными под углом друг к другу. Зная длину одного катета и угол между ними, мы можем легко найти длину троса, используя теорему Пифагора. |
| Пример 2: Определение расстояния до недоступного объекта |
| Представьте ситуацию, когда нужно определить расстояние до объекта, который находится на недоступной высоте. Можно воспользоваться прибором для измерения углов и измерить угол между горизонтальной плоскостью и линией взгляда на объект. Зная угол и длину одного катета (например, расстояние от наблюдателя до объекта), мы можем вычислить длину гипотенузы и, следовательно, расстояние до объекта. |
| Пример 3: Расчет дистанции в спорте |
| Во многих видов спорта, особенно в гольфе или стрельбе из лука, расстояние до цели играет ключевую роль. Используя угол наклона и измеряя дальность между местом, откуда следует выстрел или ударить, и целью, можно применить теорему Пифагора для определения расстояния до цели. Зная длины катетов и угол, можно легко рассчитать дистанцию и принять правильное решение. |
Альтернативные способы определения гипотенузы

В данном разделе рассмотрим несколько иных методов вычисления гипотенузы в треугольнике, основываясь на значениях его катетов и угле между ними. Эти альтернативные подходы обеспечат дополнительную гибкость при решении задач, позволяя выбирать подходящий метод в зависимости от условий. Исследуем новые формулы и их применимость в различных математических задачах.
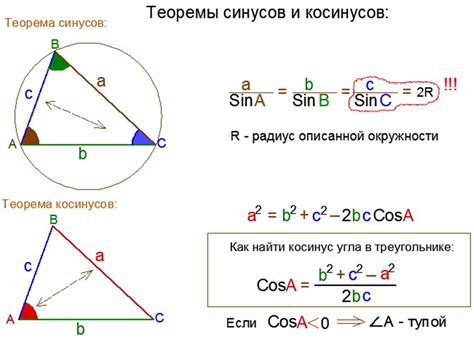
Метод с использованием теоремы косинусов
- Формула: с^2 = a^2 + b^2 - 2ab * cos(γ)
- Этот подход основывается на теореме косинусов и позволяет вычислить гипотенузу с использованием длин катетов и угла между ними.
- Пример использования: допустим, что нам известны длины катетов a = 5 и b = 8, а угол между ними γ = 45 градусов. Подставляя значения в формулу и выполняя расчеты, получаем: с^2 = 5^2 + 8^2 - 2 * 5 * 8 * cos(45°) = 25 + 64 - 80 * 0,707 ≈ 25 + 64 - 56,56 = 32,44. Отсюда найдем гипотенузу c как квадратный корень из этого значения: c ≈ √32,44 ≈ 5,7.
Метод с использованием теоремы синусов
- Формула: c = a / sin(α) = b / sin(β)
- Этот способ основывается на теореме синусов и позволяет вычислить гипотенузу с использованием длин катетов и соответствующих им углов.
- Пример использования: предположим, что нам известны длины катетов a = 3 и b = 4, а угол α между гипотенузой и катетом a составляет 30 градусов. Подставляя значения в формулу и выполняя расчеты, получаем: c = 3 / sin(30°) = 4 / sin(β). Чтобы найти угол β, воспользуемся теоремой о сумме углов треугольника: β = 180° - 30° = 150°. Теперь можем вычислить гипотенузу: c = 4 / sin(150°) ≈ 4 / 0,5 ≈ 8.
Использование тригонометрических функций для вычислений: эффективный метод расчета
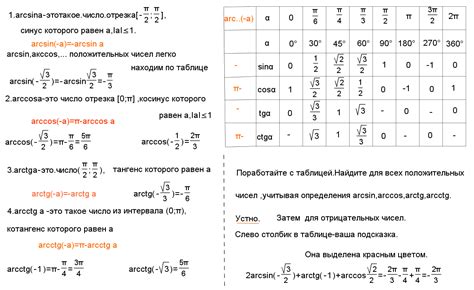
В данном разделе мы рассмотрим применение тригонометрических функций при решении задач, связанных с нахождением гипотенузы, катетов и углов треугольника. Тригонометрические функции, такие как синус, косинус и тангенс, позволяют использовать соотношения между сторонами и углами треугольника для точного вычисления их значений.
Для начала, рассмотрим теоретический аспект использования тригонометрических функций. Они основаны на соотношениях, устанавливающих зависимость между длинами сторон треугольника и значениями углов. Например, синус угла определяется как отношение противолежащего катета к гипотенузе, косинус - отношение прилежащего катета к гипотенузе, а тангенс - отношение противолежащего катета к прилежащему катету. Пользуясь этими формулами, мы можем эффективно и точно вычислить значения требуемых сторон и углов.
| Функция | Определение | Применение для расчета |
|---|---|---|
| Синус | Отношение противолежащего катета к гипотенузе | Нахождение длины противолежащего катета, если известна гипотенуза и значение угла |
| Косинус | Отношение прилежащего катета к гипотенузе | Нахождение длины прилежащего катета, если известна гипотенуза и значение угла |
| Тангенс | Отношение противолежащего катета к прилежащему катету | Нахождение значения угла, если известны длины противолежащего и прилежащего катетов |
Помимо использования тригонометрических функций для нахождения значений сторон и углов треугольника, их можно также применять при решении различных задач. Например, вычисление высоты, нахождение площади треугольника или нахождение других неизвестных величин на основе известных данных. Использование тригонометрических функций в сочетании с другими математическими методами позволяет эффективно решать разнообразные задачи связанные с треугольниками.
Специфика определения длины гипотенузы в различных типах треугольников
Когда речь заходит о нахождении гипотенузы в треугольнике, существует несколько методов, применяемых в зависимости от его типа. Каждый тип треугольника имеет свои особенности и критерии для определения гипотенузы, которые меняются в зависимости от заданных данных.
В прямоугольном треугольнике для нахождения гипотенузы используется теорема Пифагора, которая позволяет связать квадрат гипотенузы со суммой квадратов катетов. В то же время, при рассмотрении остроугольного или тупоугольного треугольника, гипотенуза вычисляется с помощью тригонометрических функций, таких как синус, косинус и тангенс. При этом, в зависимости от заданного угла, величина катета и типа треугольника, используются разные формулы.
Если треугольник является равносторонним, то все его стороны и углы равны между собой. В этом случае, для определения гипотенузы достаточно знать длину одного из катетов или любой другой стороны треугольника.
Таким образом, понимание специфики расчета гипотенузы в различных типах треугольников позволяет использовать соответствующие формулы и методики для точного определения длины гипотенузы в зависимости от заданных параметров.
Применение формулы косинусов для вычисления длины гипотенузы
Примеры вычисления гипотенузы с использованием формулы косинусов
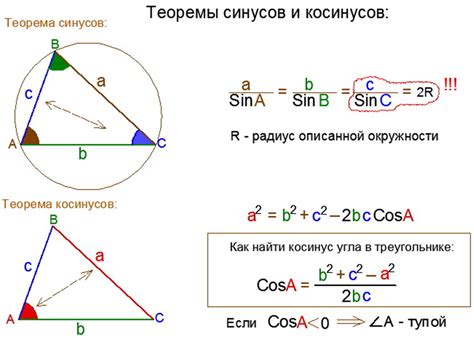
В данном разделе представлены примеры расчета гипотенузы в треугольнике с помощью формулы косинусов. Использование данного метода позволяет определить длину гипотенузы на основе известных значений длин катетов и величины угла между ними. Приведенные ниже примеры помогут разобраться в процессе расчета и подробно продемонстрируют применение формулы косинусов в практических задачах.
Пример 1:
- Дано: длина первого катета - а, длина второго катета - b и величина угла между ними - α.
- Решение: для определения гипотенузы используем формулу косинусов:
- Запишем значения из условия:
- Подставим значения в формулу и произведем вычисления:
- Ответ: гипотенуза треугольника равна примерно 5.6637.
c = √(a² + b² - 2abcosα)
a = 6, b = 8, α = 45°
c = √(6² + 8² - 2*6*8*cos45°) = √(36 + 64 - 96*0.7071) = √(36 + 64 - 67.8826) = √(32.1174) ≈ 5.6637
Пример 2:
- Дано: длина первого катета - x, длина второго катета - y и величина угла между ними - β.
- Решение: воспользуемся формулой косинусов для нахождения гипотенузы:
- Исходные данные:
- Подставим значения в формулу и выполним вычисления:
- Ответ: гипотенуза треугольника составляет примерно 8.8882.
c = √(x² + y² - 2xycosβ)
x = 7, y = 10, β = 60°
c = √(7² + 10² - 2*7*10*cos60°) = √(49 + 100 - 140*0.5) = √(149 - 70) = √(79) ≈ 8.8882
1. Расчет расстояния и пространства:
Благодаря способу нахождения гипотенузы по катетам и углу между ними, мы можем эффективно определить расстояние между двумя точками в трехмерном пространстве. Это особенно полезно при проектировании и строительстве, где точная оценка расстояний важна для успешного выполнения проекта.
2. Электроника и технологии:
Полученные знания могут быть применены в различных областях электроники и технологий. Например, при разработке схем и плат для электронных устройств, позиционировании объектов на экране компьютера или определении координат в системах глобального позиционирования (GPS).
3. Навигация и картография:
Знания о способах нахождения гипотенузы по катетам и углу между ними могут быть применены в области навигации и картографии. Определение расстояний и углов позволяет строить точные карты и навигационные системы, которые могут быть полезными для автопилотов, мореплавателей и путешественников.
Вопрос-ответ

Как найти гипотенузу треугольника по известным катетам и углу между ними?
Для вычисления гипотенузы треугольника по известным катетам и углу между ними можно использовать простой способ расчета. По теореме косинусов, квадрат гипотенузы равен сумме квадратов катетов минус произведение катета на косинус угла между ними. Формула выглядит следующим образом: c^2 = a^2 + b^2 - 2ab·cos(α), где c - гипотенуза, a и b - катеты, а α - угол между катетами.
Какие данные нужны для расчета гипотенузы треугольника по катетам и углу между ними?
Для вычисления гипотенузы треугольника по катетам и углу между ними необходимо знать длины двух катетов и величину угла между ними. Эти данные позволят воспользоваться теоремой косинусов и получить значение гипотенузы.
Есть ли более простой способ найти гипотенузу треугольника по катетам и углу между ними?
Нет, данный способ расчета по теореме косинусов является наиболее простым известным методом для определения гипотенузы треугольника по катетам и углу между ними. Используя эту формулу, можно точно и быстро получить желаемый результат.
Какие еще способы существуют для расчета гипотенузы треугольника?
Кроме метода, основанного на теореме косинусов, можно применять теорему Пифагора для определения гипотенузы треугольника. Если известны длины обоих катетов, то воспользуйтесь формулой c = sqrt(a^2 + b^2), где c - гипотенуза, а a и b - катеты. Однако, для расчета гипотенузы треугольника по катетам и углу между ними, лучше использовать теорему косинусов, так как она более универсальна и позволяет решать более широкий спектр задач.
Можно ли найти гипотенузу треугольника без знания угла между катетами?
Нет, для расчета гипотенузы треугольника необходимо знать величину угла между катетами. Это связано с тем, что значение гипотенузы зависит от угла между катетами и их длин. Без информации об угле, невозможно точно определить гипотенузу.
Как можно найти гипотенузу простым способом?
Для нахождения гипотенузы треугольника по известным катетам и углу между ними можно воспользоваться тригонометрическим соотношением. Известная формула гласит: гипотенуза = катет1 / sin(угол). Необходимо подставить значения катетов и угла в данное уравнение и произвести вычисления.



