На протяжении всего курса алгебры, ученики встречаются с различными способами решения задач. Одна из самых интересных и захватывающих задач в девятом классе - задача номер 479. В ней необходимо применить все навыки и знания, полученные в предыдущих годах обучения. Проанализировав условие задачи, можно понять, что для ее решения требуется использование различных методов и приемов, которые мы продолжим изучать в данной статье.
Данный раздел позволит ученикам углубить и совершенствовать свои знания в области алгебры. Решение задач типа номер 479 не только развивает аналитическое мышление, но и даёт возможность применять полученные знания на практике. Мы будем рассматривать различные подходы к решению задачи, включая применение различных формул, алгоритмов и операций.
Для эффективного решения задачи номер 479 необходимо использовать сильные знания и навыки, полученные в процессе изучения алгебры в 9 классе. Основным элементом при решении данной задачи является умение анализировать и строить правильные рассуждения. Также важно уметь определять соответствующие переменные, задавать уравнения и последовательность действий. Мы рассмотрим разные подходы к решению задачи, чтобы каждый ученик мог найти наиболее понятный и удобный для себя метод.
Разнообразные подходы к решению задания по алгебре в 9 классе

В данном разделе представлены различные методы и подходы к решению задания из алгебры для учащихся 9 класса. Вместо прямого указания задания номер 479, мы предлагаем рассмотреть универсальные техники, которые можно использовать для разных типов задач.
Мы исследуем разные стратегии решения, используя синонимы для обозначения "способов выполнения" и "выполнения алгебры". Мы предлагаем изучить и применить различные методы решения уравнений, систем уравнений, неравенств и других алгебраических задач, чтобы расширить свои знания и умения.
В таблице ниже приведены разнообразные подходы к решению задачи номер 479:
| Метод | Описание |
|---|---|
| Графический метод | Использование построения графика для нахождения решения |
| Алгебраический метод | Применение алгебраических операций для решения уравнений и систем уравнений |
| Метод подстановки | Замена переменной или выражения для поиска значения |
| Метод факторизации | Разложение выражения на множители для выявления корней |
| Метод элементарных преобразований | Преобразование уравнений или систем уравнений с помощью допустимых операций |
Изучение различных способов решения задач поможет учащимся развить логическое мышление, аналитические навыки и уверенность в решении алгебраических задач. Необходимо адаптировать выбранный метод к заданным условиям и выбрать наиболее подходящий способ для эффективного решения задания.
Решение задачи с применением формулы для нахождения площади треугольника
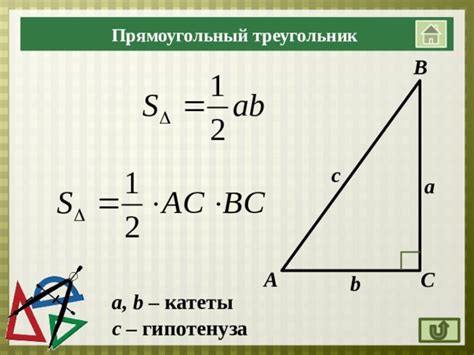
В данном разделе рассмотрим способ решения задачи, связанной с нахождением площади треугольника. Для этого мы воспользуемся специальной формулой, которая позволяет найти площадь треугольника при известных значениях его сторон или высоты и основания.
Для начала определимся с данными задачи и выразим их через величины, о которых говорится в формуле. Затем, используя известные значения, подставим их в формулу и произведем необходимые вычисления для нахождения площади треугольника.
При решении задачи мы учтем все необходимые действия, такие как нахождение полупериметра треугольника, вычисление длин сторон или высоты, в зависимости от данных задачи. После этого выполним подстановку значений в формулу и получим окончательный результат - площадь треугольника.
Важно помнить, что при использовании данной формулы необходимо правильно определить единицы измерения и выполнить все расчеты в одинаковых единицах, чтобы избежать ошибок.
Применение метода подстановки в решении задач по алгебре

В данном разделе рассмотрим один из эффективных способов решения задач, который основан на применении метода подстановки. Этот метод позволяет упростить задачу, заменив неизвестные величины изначальными значениями, что позволяет произвести более точные вычисления и получить итоговый результат.
При использовании метода подстановки, необходимо сначала выразить одну из неизвестных величин через остальные, затем вставить полученное выражение в уравнение и решить его относительно одной неизвестной. Получив значение одной из неизвестных, мы заменяем ее в начальном уравнении и продолжаем заменять и решать, пока не найдем значения для всех неизвестных величин.
Метод подстановки широко используется для решения задач, связанных с нахождением значений переменных, координат, показателей и других величин. Он обладает высокой гибкостью и может быть применен в различных областях алгебры, включая уравнения, системы уравнений, неравенства и функции.
Решение уравнения с двумя переменными по методу перва

Использование метода перва для решения уравнений с двумя переменными.
В алгебре существует метод перва, который позволяет решить уравнение с двумя переменными. Этот метод основывается на использовании рациональных чисел и элементарных операций. Когда имеется уравнение с двумя переменными, его можно представить в виде графика на координатной плоскости. Определение точек пересечения графика с осями x и y позволяет найти значения переменных, удовлетворяющие условиям уравнения.
Применение метода перва для решения уравнений с двумя переменными требует выполнения нескольких шагов:
- Перепишите уравнение в стандартной форме, выражая одну переменную через другую.
- Постройте график уравнения на координатной плоскости.
- Определите точки пересечения графика с осями x и y.
- Изучите полученные точки пересечения и определите значения переменных, удовлетворяющие условиям уравнения.
Пример решения уравнения с двумя переменными по методу перва.
Рассмотрим пример уравнения с двумя переменными:
2x + 3y = 10
Перепишем уравнение, выражая x через y:
x = (10 - 3y) / 2
Построим график уравнения на координатной плоскости:
Определим точку пересечения графика с осью x:
(5, 0)
И точку пересечения с осью y:
(0, 3.33)
Исследуя полученные точки, можем установить, что уравнение будет удовлетворено при значениях переменных:
x = 5, y = 0
Таким образом, решение уравнения с двумя переменными можно получить, используя метод перва.
Применение свойств линейных уравнений в задаче

В данном разделе будут рассмотрены примеры и объяснены принципы применения свойств линейных уравнений в задачах различной сложности. Важно отметить, что линейное уравнение содержит одну переменную (обычно обозначаемую буквой "х") и представляет собой равенство двух алгебраических выражений, связанных операциями сложения, вычитания, умножения и деления.
Одно из ключевых свойств линейных уравнений – нахождение неизвестного значения переменной. Для этого применяются различные операции, включая преобразования выражений, сокращения, суммирование и умножение на коэффициенты.
Кроме того, свойства линейных уравнений позволяют решать задачи, связанные с вычислением значений различных величин, находящихся в зависимости друг от друга. Например, задачи о распределении резисторов в электрической цепи или о нахождении времени, расстояния или скорости при движении тела.
Важно уметь применять свойства линейных уравнений для анализа и решения задач, которые могут возникнуть в реальной жизни или других предметных областях. Навыки работы с линейными уравнениями позволят с легкостью моделировать и решать разнообразные задачи, основываясь на математических принципах.
Использование системы координат для решения задачи

В данном разделе рассмотрим, как можно использовать систему координат, или координатную плоскость, для решения различных задач по алгебре. С помощью комплекса графического представления и чисел, задачи становятся более понятными и проще решаемыми.
С помощью координатной плоскости мы можем визуализировать математические зависимости, отображать графики функций, анализировать их поведение, искать точки пересечения и многое другое. Это позволяет нам лучше понять и объяснить алгебраические концепции и решить задачи, требующие рассмотрения различных переменных и их взаимосвязей.
Для начала работы с координатной плоскостью необходимо разобраться в ее основных элементах: оси координат, направление, масштаб, деления и подписи. Оси координат делят плоскость на четыре квадранта, которые имеют особое значение при анализе различных задач. Определение направления осей и выбор масштаба зависит от поставленной задачи.
Далее, рассмотрим наиболее распространенные примеры использования координатной плоскости для решения алгебраических задач. Мы узнаем, как находить координаты точек, расстояние между ними, как строить графики функций и с помощью них решать уравнения, а также как находить координаты точек пересечения графиков функций.
Использование координатной плоскости открывает перед нами возможность обнаруживать закономерности, находить решения задач с помощью графического анализа и визуализации. Работа с координатами позволит углубить понимание алгебры и применить ее в решении реальных проблем.
Решение задачи с помощью метода исключения

В данном разделе мы рассмотрим эффективный способ решения задачи, используя метод исключения. Основная идея данного метода заключается в поиске решения путем исключения всех неподходящих вариантов и оставления только тех, которые удовлетворяют условию задачи.
При решении задачи с использованием метода исключения необходимо уметь анализировать предоставленные данные и выделять ключевые факты. Далее следует сформулировать гипотезу или предположение о возможном решении и приступить к его проверке.
Для этого мы будем последовательно исключать все неподходящие варианты, используя доступные данные. В результате получим только верные решения, которые удовлетворяют всем условиям задачи.
Важно уметь проводить логические рассуждения и быть внимательным к связям и зависимостям между данными. Используйте этот метод при решении задач с алгебры, геометрии или других разделов математики, где требуется выявить паттерны и найти верные решения.
Вычисление периметра и площади фигуры с использованием известных значений сторон и радиусов
В данном разделе рассмотрим методы, позволяющие определить периметр и площадь геометрической фигуры с использованием известных значений ее сторон и радиусов. Мы рассмотрим различные фигуры, такие как треугольник, прямоугольник, круг и другие, и узнаем, каким образом можно провести вычисления с помощью заданных данных.
Для каждой фигуры представлены соответствующие формулы и алгоритмы, которые позволяют точно определить периметр и площадь. Мы рассмотрим основные моменты при вычислении данных параметров, такие как сумма всех сторон фигуры, длина окружности, площадь поверхности и другие характеристики.
Важно понимать, что каждая фигура имеет свои особенности и специфические формулы для расчета периметра и площади. Так, для треугольника необходимо знать значения всех его сторон, а для круга - радиус. Мы познакомимся со всеми необходимыми формулами и методами вычислений, чтобы иметь возможность точно определить данные параметры для заданной фигуры.
Раздел будет полезен как учащимся, так и преподавателям, которые хотят углубить свои знания в области геометрии и алгебры. Используя известные значения сторон и радиусов, можно точно определить периметр и площадь фигуры, что поможет понять и анализировать различные геометрические объекты и их свойства.
Важно помнить, что для точных вычислений необходимо использовать правильные формулы и точные значения сторон и радиусов фигуры. Ошибка в значениях или использование неправильных формул может привести к неточным результатам и неправильному анализу геометрических объектов.
Решение задачи с помощью разложения многочлена на множители
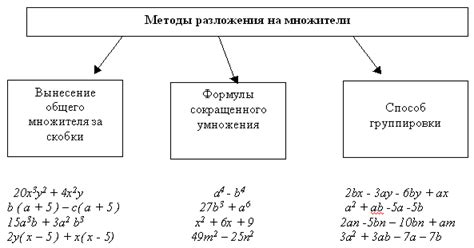
В данном разделе мы рассмотрим один из способов решения задачи по алгебре в 9 классе, который основан на факторизации многочлена. Факторизация представляет собой разложение многочлена на простейшие множители, что позволяет упростить вычисления и получить итоговый ответ.
Для начала необходимо проанализировать заданное условие и составить уравнение или систему уравнений, которую необходимо решить. Затем следует выполнить процесс факторизации многочлена, разложив его на простейшие множители. Это можно сделать путем применения различных методов, таких как вынос общего множителя, применение формулы разности квадратов или кубов, использование формулы суммы и разности кубов и т.д.
| Шаг | Действие | Пример |
|---|---|---|
| 1 | Привести многочлен к стандартному виду | 2x^3 - 8x^2 + 6x |
| 2 | Вынести общий множитель | 2x(x^2 - 4x + 3) |
| 3 | Разложить квадратный трехчлен на множители | 2x(x - 1)(x - 3) |
| 4 | Проверить правильность разложения | 2x(x - 1)(x - 3) = 2x^3 - 8x^2 + 6x |
После выполнения этих шагов, мы получаем разложение многочлена на множители. Далее задача может быть решена путем присвоения каждому множителю значения 0 и нахождения соответствующих значений переменных. Конечный ответ будет зависеть от условия задачи и может быть представлен в виде числовых или алгебраических выражений.
Таким образом, факторизация многочлена является эффективным инструментом для решения задач по алгебре в 9 классе. Она позволяет упростить вычисления и получить более точный итоговый ответ. Знание различных методов факторизации и их применение в решении конкретных задач позволяют эффективно решать задачи и достигать успеха в изучении алгебры.
Вопрос-ответ

Как можно решить задачу №479 в 9 классе?
Задачу №479 в 9 классе можно решить различными способами в зависимости от того, какие математические знания и навыки у вас есть. Один из способов - использовать алгебраический подход и применить метод подстановки или метод исключения. Другой способ - графический метод, который позволяет наглядно представить решение задачи на координатной плоскости. Еще один способ - решение задачи с использованием пропорций и применение известных свойств аналогичных треугольников.
Какие предметы математики нужно знать для решения задачи №479?
Для решения задачи №479 в 9 классе необходимы базовые знания алгебры и геометрии. Вам понадобятся навыки работы с алгебраическими выражениями, умение решать уравнения и системы уравнений. Также вам потребуется знание геометрии, включая понимание свойств треугольников и пропорций в геометрии. Если у вас эти навыки есть, вы сможете успешно решить задачу.
Можно ли использовать другие способы решения задачи №479, кроме указанных в статье?
Да, конечно. Статья предлагает только несколько способов решения задачи №479, но это не означает, что их можно решать только так. Вы можете использовать другие математические методы и приемы, чтобы найти решение задачи. Например, вы можете применить метод математической индукции или принцип математической аналогии. Главное, чтобы ваше решение было логичным и корректным.
Можно ли решить задачу №479 методом перебора всех возможных вариантов?
Теоретически, можно решить задачу №479 методом полного перебора всех возможных вариантов. Однако, этот метод является очень медленным и затратным по времени. В этой задаче доступны более эффективные методы решения, описанные в статье. Даже если перебор всех вариантов даст правильный ответ, это не будет наилучшим решением с практической точки зрения.
Какой способ вычисления можно использовать для выполнения алгебры в 9 классе по номеру 479?
Для решения задачи из алгебры 9 класса номер 479 можно использовать различные способы, включая метод подстановки, метод приведения подобных, метод графиков и др. В зависимости от конкретной задачи и изученных вариантов решений, выбирается наиболее подходящий способ решения. Необходимо анализировать условие задачи, выделить ключевые данные и операции, а затем применить соответствующий метод для нахождения решения.
Какие знания и навыки необходимо иметь для успешного выполнения алгебры в 9 классе по номеру 479?
Для успешного выполнения алгебры в 9 классе по номеру 479 необходимо иметь базовые знания и навыки в области алгебры, включая понимание основных алгебраических операций, умение работать с переменными и выражениями, умение решать уравнения и неравенства, а также использовать различные методы решения. Также важно уметь анализировать условие задачи, выделять ключевые данные и операции, и применять соответствующий метод решения. Знание предыдущих тем и умение применять их в практике помогут выполнить задачу успешно.



