Рассмотрение и понимание принципиальных аспектов логических структур населено сложностями и неоднозначностями. Одной из таких проблем является определение тавтологии функции, которое требует основательного анализа и поиска логической безошибочности. Исследование данной проблемы затрагивает важный аспект логического рассуждения, который способен пролить свет на неочевидные зависимости и закономерности в математических функциях.
Когда речь заходит о тавтологии функции, следует учитывать, что данное понятие является своеобразной связующей нитью между математикой и логикой. Тавтология функции представляет собой особый вид логической зависимости, при которой истинность высказывания подтверждается не зависимо от значений переменных, на которые оно опирается.
Таким образом, важно понимать, что анализ тавтологии функции необходим для разоблачения потенциальных ошибок в математических доказательствах и формализованных системах. Внимательное изучение данного явления поможет выявить строение и связи функций, а также пролить свет на возможные ограничения математического мышления. Именно поэтому изучение тавтологии функции является неотъемлемой частью логического анализа и математического исследования в целом.
Фундаментальная суть тавтологии функции

- Следовательно, тавтология функции - это такое структурированное математическое выражение или утверждение, которое, вне зависимости от значения своих переменных, всегда возвращает тот же результат. Она является непоколебимым фундаментом истинности, неизбежным законом.
Таким образом, тавтология функции представляет собой специальное явление, позволяющее нам касаться граней неизменной истины и открывая новые перспективы для развития науки и математики. Благодаря своей всеобъемлющей природе, тавтология функции играет ключевую роль в построении логических систем, помогая нам более глубоко понять и объяснить законы и принципы, лежащие в основе многих отраслей научного исследования.
Принципы выявления всегда истинных выражений в функции
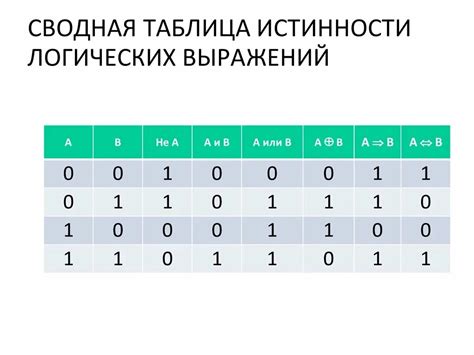
В ходе анализа и проверки функции на наличие тавтологии, важно определить такие выражения, которые гарантированно истинны независимо от значений переменных в функции. Для этого необходимо установить общие правила и признаки, которые помогут нам выделить такие выражения. Данные правила позволяют определить, когда функция становится тавтологией.
Один из важных принципов в определении тавтологии - это нахождение тавтологических формул, в которых каждое выражение всегда истинно, не зависящее от значений переменных. Тавтологические формулы не только упрощают логические выражения, но и помогают установить несостоятельные утверждения в функции.
Кроме того, следует обратить внимание на правило подстановки, которое позволяет заменять одни переменные на другие в выражении функции. При этом, если после подстановки выражение всегда является истинным, то это может сигнализировать о тавтологии в функции.
Другим важным принципом является анализ структуры логических операций в функции. Определенные комбинации этих операций могут приводить к тавтологии, и поэтому важно исследовать их на предмет возможности всегда истинного значения.
Наконец, в процессе определения тавтологии нужно учитывать связь между переменными в функции. Если существуют определенные зависимости, которые всегда приводят к истинным значениям, то это может указывать на наличие тавтологии. Знание соотношений между переменными и их взаимодействия играет важную роль в процессе анализа функции.
Как проверить функцию на тавтологию?

- Анализ истинности функции: Первый способ проверки функции на тавтологию заключается в анализе ее истинности. Для этого необходимо составить таблицу истинности, где в каждой строке будут перечислены все возможные комбинации входных значений функции. Затем необходимо вычислить значения функции для каждой комбинации и проверить, что на выходе всегда получается истинное значение. Если это происходит для всех комбинаций, то функция является тавтологией.
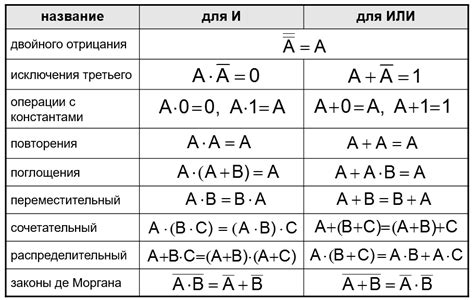
- Применение законов логики: Второй способ проверки функции на тавтологию заключается в применении законов логики. Законы логики позволяют проводить различные преобразования и упрощения функций. Если после применения законов логики функция приводится к тривиальной форме, например, всегда является истинной или всегда является ложной, то она является тавтологией.
- Доказательство от противного: Третий способ проверки функции на тавтологию основывается на методе доказательства от противного. Допустим, мы предполагаем, что функция не является тавтологией. Затем, применяя законы логики и логические преобразования, мы пытаемся создать комбинацию входных значений, при которой функция станет ложной. Если нам удается это сделать, то предположение было неверным, и функция является тавтологией. Если же нам не удается найти такую комбинацию, то функция действительно является тавтологией.
Таким образом, проверка функции на тавтологию - это важный этап в логике и математике. Она позволяет определить, является ли функция истинной во всех возможных случаях. Для этого можно использовать анализ истинности функции, применение законов логики или метод доказательства от противного. Важно знать эти способы и уметь применять их для эффективной работы с функциями.
Примеры логических выражений, которые всегда истинны или всегда ложны
Одним из примеров тавтологий является выражение "A или не A". Независимо от значений переменной А, данное утверждение всегда будет истинным. Можно использовать синоним "любое значение А или противоположное ему значение А всегда истинно".
Еще одним примером тавтологии является "A или A". В данном случае, независимо от значений переменной А, данное утверждение всегда будет ложным. Вариант синонима: "Оба значения А и противоположное ему значение А всегда ложны".
Также стоит обратить внимание на выражение "A → A", где символ "→" означает импликацию (если...то...). В этом случае, независимо от значения переменной А, данное утверждение всегда будет истинным. Синоним: "Значение А всегда влечет за собой значение А".
Рассмотрение и понимание примеров тавтологических функций поможет улучшить понимание логических выражений и развить навыки логического мышления.
Практическое применение логической истинности в программировании

Рациональное использование логической истинности, или тавтологии, в программировании может значительно упростить разработку кода и повысить его надежность. Отталкиваясь от аксиомы, что истинность невозможно опровергнуть, программисты могут использовать эту логическую особенность для достижения более эффективного выполнения задач.
Одним из практических применений тавтологии в программировании является использование условных операторов для принятия решений в зависимости от верности определенных утверждений. Логическое выражение, которое всегда является истинным, может быть полезным для определения установки граничных условий или выполнения определенных действий при отсутствии конкретных данных.
Также тавтология может быть применена при разработке алгоритмов, где гарантированная верность некоторых логических утверждений является предпосылкой для корректности работы программы. Например, проверка на истинность определенных значений переменных может помочь программе избежать ошибок или некорректных действий во время выполнения.
Практическое использование тавтологии также встречается в тестировании программного обеспечения. Логические утверждения, которые всегда являются истинными или ложными, могут использоваться для проверки корректности работы программы в различных сценариях. Это позволяет обнаружить возможные ошибки, исключения или неожиданные поведения, которые могут возникнуть в результате некорректной логики программы.
Полезные советы для распознавания повторения в функциях
В данном разделе рассмотрим некоторые подходы и техники, которые помогут вам определить повторяющиеся паттерны или тавтологии в функциях, без необходимости использования конкретных определений. Научитесь распознавать общие черты и повторяющиеся элементы в коде, что поможет вам повысить его эффективность и легкость поддержки.
| Совет | Описание |
|---|---|
| 1. Изучите область применения функции | Понимание для чего используется функция поможет выявить возможные тавтологии, так как они могут проявляться в повторении одних и тех же операций или шаблонов. |
| 2. Обратите внимание на аргументы функции | Анализ аргументов функции может помочь обнаружить повторяющиеся элементы или паттерны, которые могут быть вынесены из функции и абстрагированы в отдельные компоненты. |
| 3. Изучите внутреннюю реализацию функции | Взгляните на содержимое функции и обратите внимание на повторяющиеся фрагменты кода, которые могут быть выделены в отдельные функции или использованы более элегантные решения. |
| 4. Проведите анализ зависимостей функции | Установите, какие части кода или модули используют данную функцию. Повторное использование этой функции в разных местах может указывать на тавтологии или неправильное проектирование кода. |
| 5. Примените принцип DRY (Don't Repeat Yourself) | Ищите повторяющиеся фрагменты кода в функции и старайтесь вынести их в отдельные функции или классы для повышения его читаемости и улучшения повторного использования. |
Следование указанным советам поможет выявить повторения и определить тавтологии в функциях, улучшая их эффективность и поддержку в долгосрочной перспективе.
Вопрос-ответ

Что такое тавтология функции?
Тавтология функции - это логическое выражение, которое всегда истинно независимо от значений своих переменных.
Как определить, является ли функция тавтологией?
Для определения тавтологии функции необходимо составить ее таблицу истинности и проверить, будет ли она истинна при всех возможных значениях переменных.
Какое значение имеет тавтология функции в логике?
Тавтология функции является фундаментальным понятием в логике и имеет большое значение при доказательстве теорем и построении логических систем.
Какие есть примеры тавтологии функции?
Примеры тавтологий функций включают в себя выражения вида (p ∨ ¬p) и (q → q).
Какие свойства обладает тавтология функции?
Тавтология функции обладает такими свойствами, как истинность при всех значениях переменных, а также сохранение истинности при логических операциях.
Что такое тавтология функции?
Тавтология функции - это случай, когда значение функции определяется исключительно значением ее аргументов. Другими словами, если значения аргументов функции достаточно для определения значения функции независимо от каких-либо дополнительных условий, то такая функция является тавтологией.



